Fair Interpretable Learning via Correction Vectors
Paper and Code
Jan 17, 2022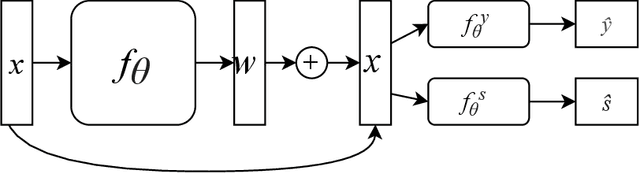
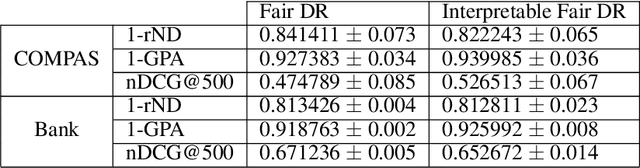

Neural network architectures have been extensively employed in the fair representation learning setting, where the objective is to learn a new representation for a given vector which is independent of sensitive information. Various "representation debiasing" techniques have been proposed in the literature. However, as neural networks are inherently opaque, these methods are hard to comprehend, which limits their usefulness. We propose a new framework for fair representation learning which is centered around the learning of "correction vectors", which have the same dimensionality as the given data vectors. The corrections are then simply summed up to the original features, and can therefore be analyzed as an explicit penalty or bonus to each feature. We show experimentally that a fair representation learning problem constrained in such a way does not impact performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge