Fair Interpretable Representation Learning with Correction Vectors

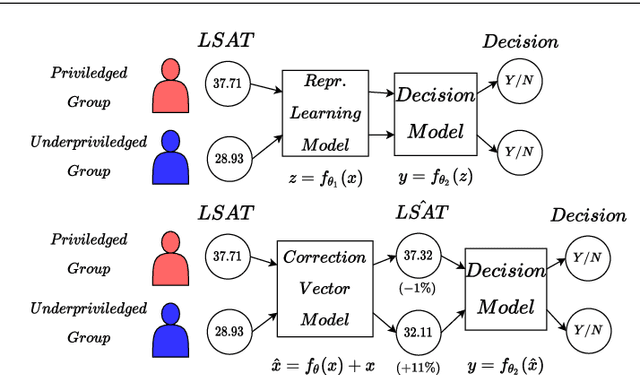
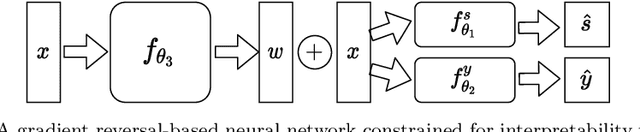
Neural network architectures have been extensively employed in the fair representation learning setting, where the objective is to learn a new representation for a given vector which is independent of sensitive information. Various representation debiasing techniques have been proposed in the literature. However, as neural networks are inherently opaque, these methods are hard to comprehend, which limits their usefulness. We propose a new framework for fair representation learning that is centered around the learning of "correction vectors", which have the same dimensionality as the given data vectors. Correction vectors may be computed either explicitly via architectural constraints or implicitly by training an invertible model based on Normalizing Flows. We show experimentally that several fair representation learning models constrained in such a way do not exhibit losses in ranking or classification performance. Furthermore, we demonstrate that state-of-the-art results can be achieved by the invertible model. Finally, we discuss the law standing of our methodology in light of recent legislation in the European Union.

Fair Interpretable Learning via Correction Vectors

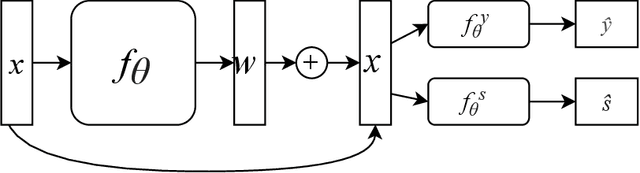
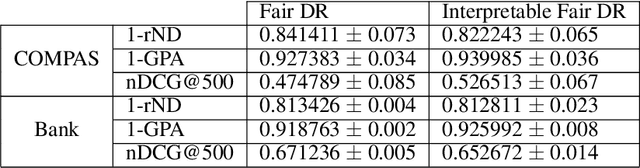
Neural network architectures have been extensively employed in the fair representation learning setting, where the objective is to learn a new representation for a given vector which is independent of sensitive information. Various "representation debiasing" techniques have been proposed in the literature. However, as neural networks are inherently opaque, these methods are hard to comprehend, which limits their usefulness. We propose a new framework for fair representation learning which is centered around the learning of "correction vectors", which have the same dimensionality as the given data vectors. The corrections are then simply summed up to the original features, and can therefore be analyzed as an explicit penalty or bonus to each feature. We show experimentally that a fair representation learning problem constrained in such a way does not impact performance.

Fair Group-Shared Representations with Normalizing Flows

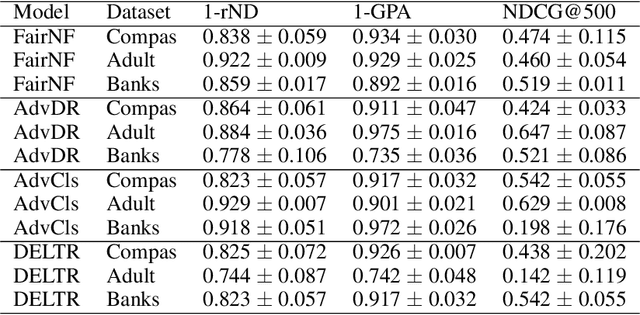
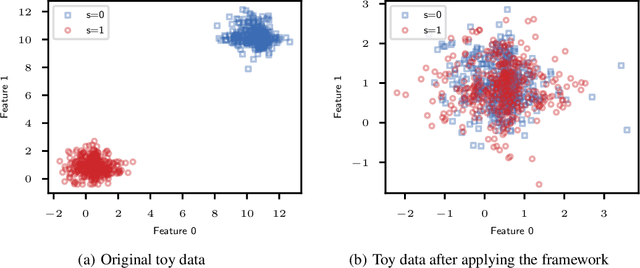
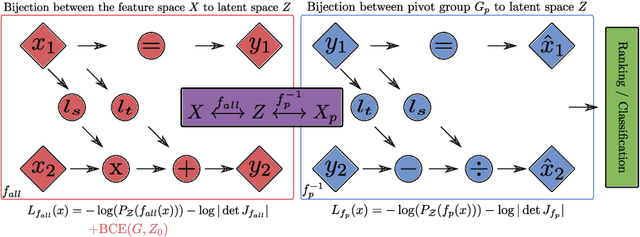
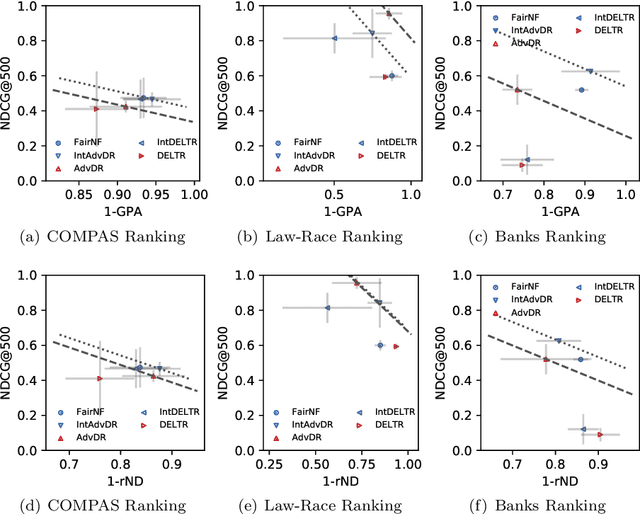
The issue of fairness in machine learning stems from the fact that historical data often displays biases against specific groups of people which have been underprivileged in the recent past, or still are. In this context, one of the possible approaches is to employ fair representation learning algorithms which are able to remove biases from data, making groups statistically indistinguishable. In this paper, we instead develop a fair representation learning algorithm which is able to map individuals belonging to different groups in a single group. This is made possible by training a pair of Normalizing Flow models and constraining them to not remove information about the ground truth by training a ranking or classification model on top of them. The overall, ``chained'' model is invertible and has a tractable Jacobian, which allows to relate together the probability densities for different groups and ``translate'' individuals from one group to another. We show experimentally that our methodology is competitive with other fair representation learning algorithms. Furthermore, our algorithm achieves stronger invariance w.r.t. the sensitive attribute.

Pairwise Learning to Rank by Neural Networks Revisited: Reconstruction, Theoretical Analysis and Practical Performance

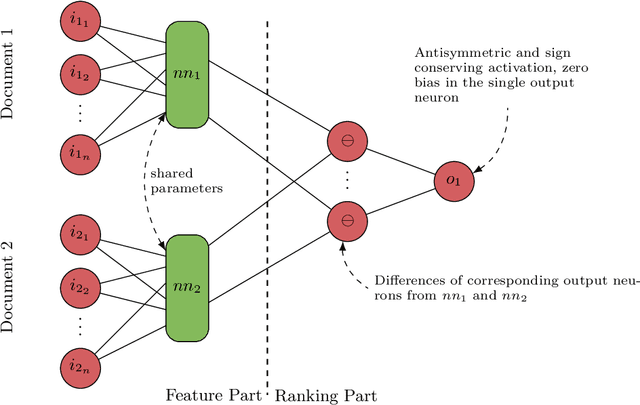
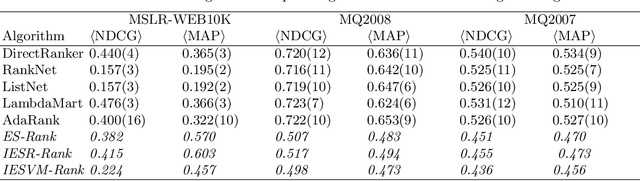
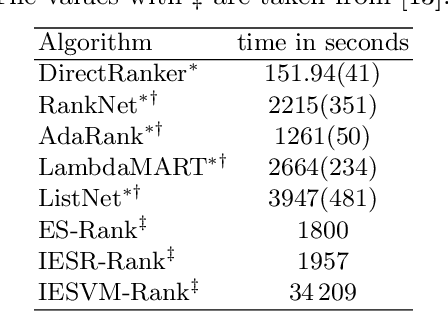
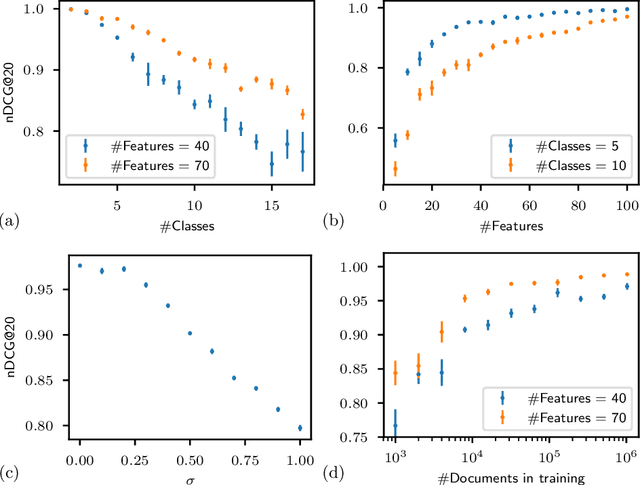
We present a pairwise learning to rank approach based on a neural net, called DirectRanker, that generalizes the RankNet architecture. We show mathematically that our model is reflexive, antisymmetric, and transitive allowing for simplified training and improved performance. Experimental results on the LETOR MSLR-WEB10K, MQ2007 and MQ2008 datasets show that our model outperforms numerous state-of-the-art methods, while being inherently simpler in structure and using a pairwise approach only.