Alesia Vallenas Coronel
Fair Interpretable Representation Learning with Correction Vectors
Feb 07, 2022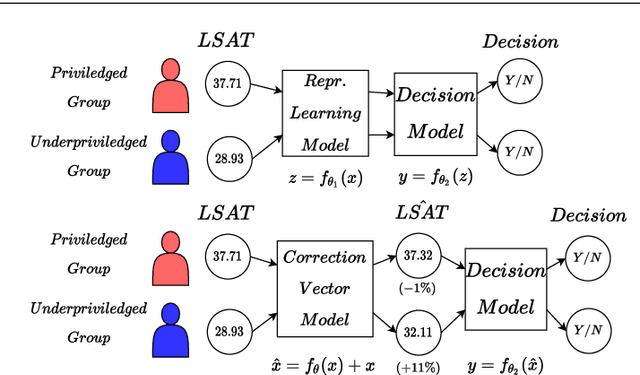
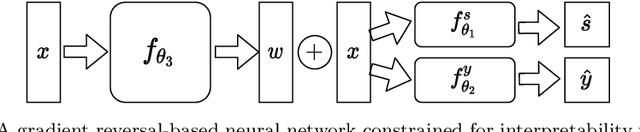
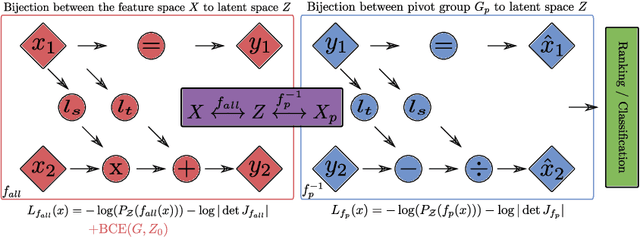
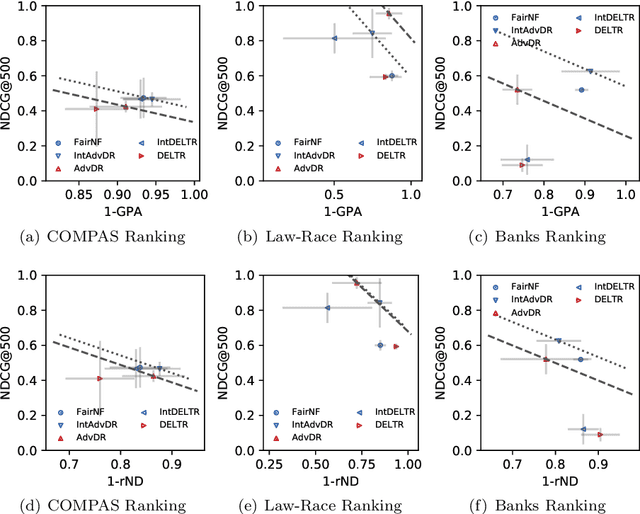
Abstract:Neural network architectures have been extensively employed in the fair representation learning setting, where the objective is to learn a new representation for a given vector which is independent of sensitive information. Various representation debiasing techniques have been proposed in the literature. However, as neural networks are inherently opaque, these methods are hard to comprehend, which limits their usefulness. We propose a new framework for fair representation learning that is centered around the learning of "correction vectors", which have the same dimensionality as the given data vectors. Correction vectors may be computed either explicitly via architectural constraints or implicitly by training an invertible model based on Normalizing Flows. We show experimentally that several fair representation learning models constrained in such a way do not exhibit losses in ranking or classification performance. Furthermore, we demonstrate that state-of-the-art results can be achieved by the invertible model. Finally, we discuss the law standing of our methodology in light of recent legislation in the European Union.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge