Marco Locatelli
Expert-Guided POMDP Learning for Data-Efficient Modeling in Healthcare
Nov 18, 2025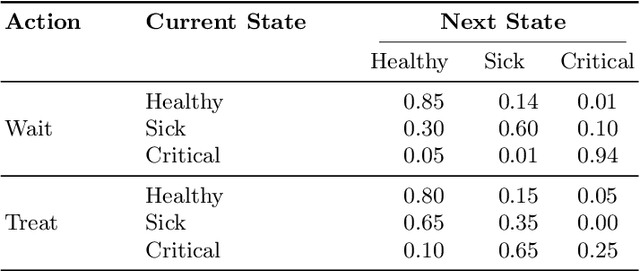
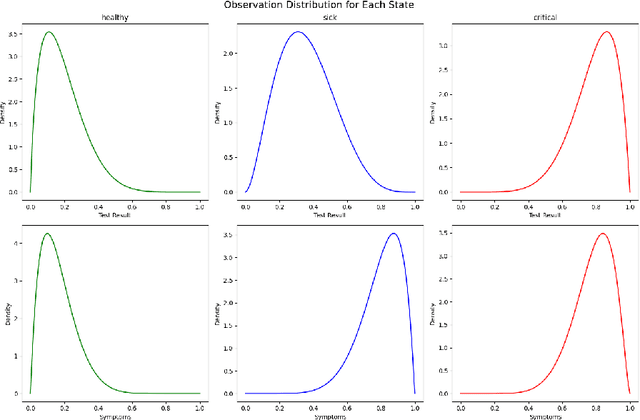
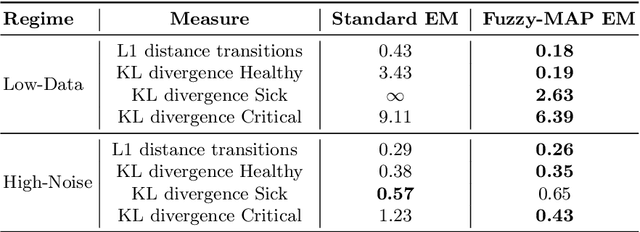
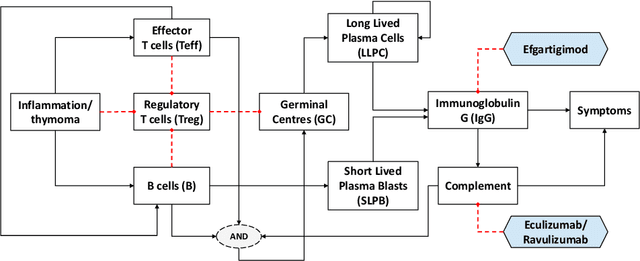
Abstract:Learning the parameters of Partially Observable Markov Decision Processes (POMDPs) from limited data is a significant challenge. We introduce the Fuzzy MAP EM algorithm, a novel approach that incorporates expert knowledge into the parameter estimation process by enriching the Expectation Maximization (EM) framework with fuzzy pseudo-counts derived from an expert-defined fuzzy model. This integration naturally reformulates the problem as a Maximum A Posteriori (MAP) estimation, effectively guiding learning in environments with limited data. In synthetic medical simulations, our method consistently outperforms the standard EM algorithm under both low-data and high-noise conditions. Furthermore, a case study on Myasthenia Gravis illustrates the ability of the Fuzzy MAP EM algorithm to recover a clinically coherent POMDP, demonstrating its potential as a practical tool for data-efficient modeling in healthcare.
Multi-Agent Path Finding on Strongly Connected Digraphs: feasibility and solution algorithms
Sep 09, 2022



Abstract:On an assigned graph, the problem of Multi-Agent Pathfinding (MAPF) consists in finding paths for multiple agents, avoiding collisions. Finding the minimum-length solution is known to be NP-hard, and computation times grows exponentially with the number of agents. However, in industrial applications, it is important to find feasible, suboptimal solutions, in a time that grows polynomially with the number of agents. Such algorithms exist for undirected and biconnected directed graphs. Our main contribution is to generalize these algorithms to the more general case of strongly connected directed graphs. In particular, given a MAPF problem with at least two holes, we present an algorithm that checks the problem feasibility in linear time with respect to the number of nodes, and provides a feasible solution in polynomial time.
Partitioned Least Squares
Jun 29, 2020



Abstract:In this paper we propose a variant of the linear least squares model allowing practitioners to partition the input features into groups of variables that they require to contribute similarly to the final result. The output allows practitioners to assess the importance of each group and of each variable in the group. We formally show that the new formulation is not convex and provide two alternative methods to deal with the problem: one non-exact method based on an alternating least squares approach; and one exact method based on a reformulation of the problem using an exponential number of sub-problems whose minimum is guaranteed to be the optimal solution. We formally show the correctness of the exact method and also compare the two solutions showing that the exact solution provides better results in a fraction of the time required by the alternating least squares solution (assuming that the number of partitions is small). For the sake of completeness, we also provide an alternative branch and bound algorithm that can be used in place of the exact method when the number of partitions is too large, and a proof of NP-completeness of the optimization problem introduced in this paper.
Globally Optimal Registration based on Fast Branch and Bound
Jan 28, 2019



Abstract:The problem of planar registration consists in finding the transformation that better aligns two point sets. In our setting, the search domain is the set of planar rigid transformations and the objective function is the sum of the distances between each point of the transformed source set and the destination set. We propose a novel Branch and Bound (BnB) method for finding the globally optimal solution. The algorithm recursively splits the search domain into boxes and computes an upper and a lower bound for the minimum value of the restricted problem. We present two main contributions. First, we define two lower bounds. The cheap bound consists of the sum of the minimum distances between each point of source point set, transformed according to current box, and all the candidate points in the destination point set. The relaxation bound corresponds to the solution of a concave relaxation of the objective function based on the linearization of the distance. In large boxes, the cheap bound is a better approximation of the function minimum, while, in small boxes, the relaxation bound is much more accurate. Second, we present a queue-based algorithm that considerably speeds up the computation.
A fast speed planning algorithm for robotic manipulators
Oct 03, 2018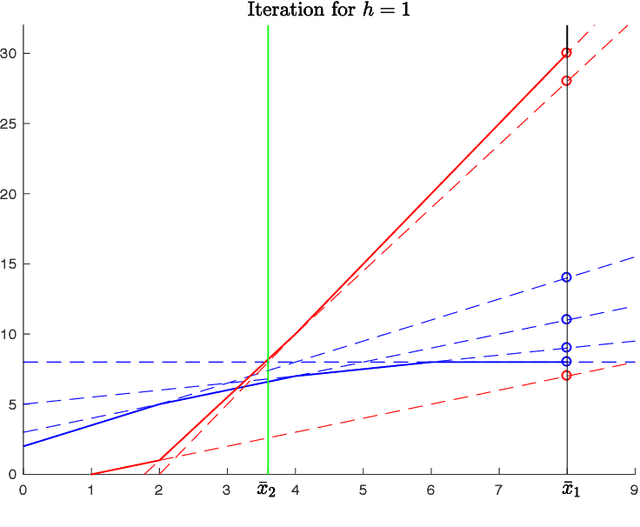

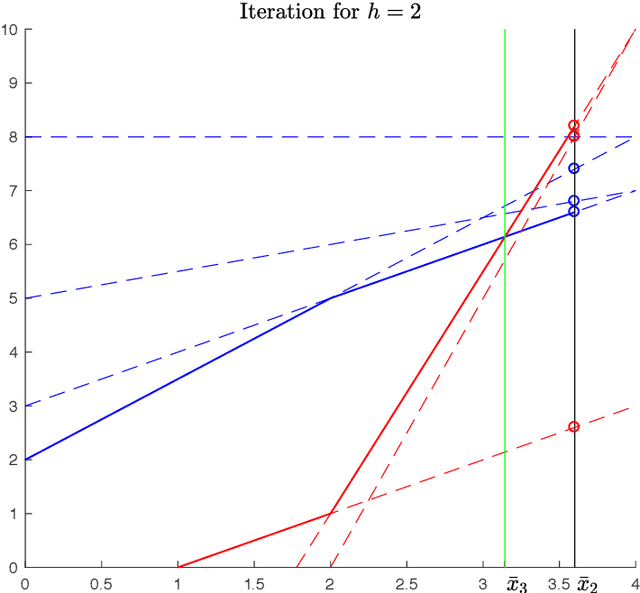
Abstract:We consider the speed planning problem for a robotic manipulator. In particular, we present an algorithm for finding the time-optimal speed law along an assigned path that satisfies velocity and acceleration constraints and respects the maximum forces and torques allowed by the actuators. The addressed optimization problem is a finite dimensional reformulation of the continuous-time speed optimization problem, obtained by discretizing the speed profile with N points. The proposed algorithm has linear complexity with respect to N and to the number of degrees of freedom. Such complexity is the best possible for this problem. Numerical tests show that the proposed algorithm is significantly faster than algorithms already existing in literature.
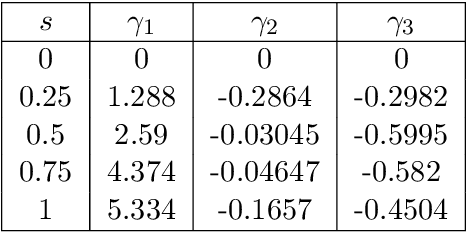
An inflationary differential evolution algorithm for space trajectory optimization
Apr 25, 2011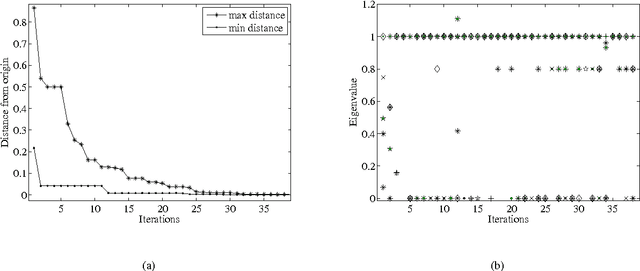
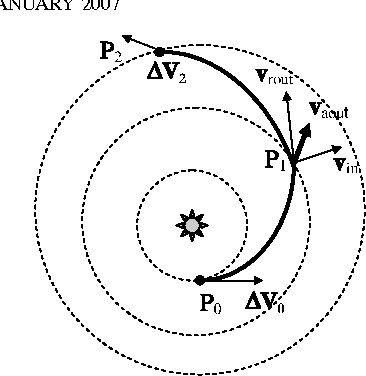
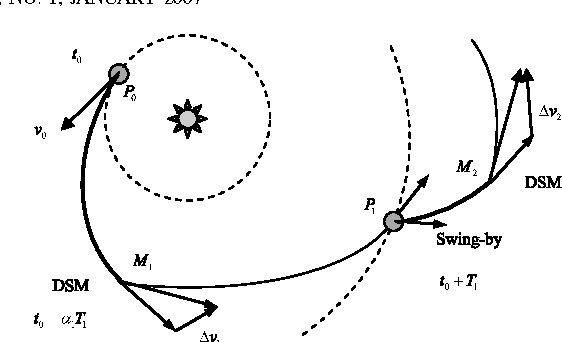
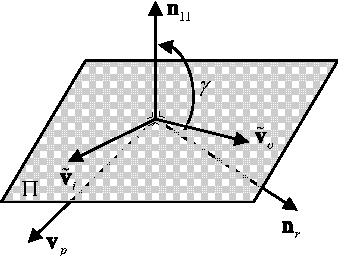
Abstract:In this paper we define a discrete dynamical system that governs the evolution of a population of agents. From the dynamical system, a variant of Differential Evolution is derived. It is then demonstrated that, under some assumptions on the differential mutation strategy and on the local structure of the objective function, the proposed dynamical system has fixed points towards which it converges with probability one for an infinite number of generations. This property is used to derive an algorithm that performs better than standard Differential Evolution on some space trajectory optimization problems. The novel algorithm is then extended with a guided restart procedure that further increases the performance, reducing the probability of stagnation in deceptive local minima.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge