Cross-Format Retrieval-Augmented Generation in XR with LLMs for Context-Aware Maintenance Assistance

This paper presents a detailed evaluation of a Retrieval-Augmented Generation (RAG) system that integrates large language models (LLMs) to enhance information retrieval and instruction generation for maintenance personnel across diverse data formats. We assessed the performance of eight LLMs, emphasizing key metrics such as response speed and accuracy, which were quantified using BLEU and METEOR scores. Our findings reveal that advanced models like GPT-4 and GPT-4o-mini significantly outperform their counterparts, particularly when addressing complex queries requiring multi-format data integration. The results validate the system's ability to deliver timely and accurate responses, highlighting the potential of RAG frameworks to optimize maintenance operations. Future research will focus on refining retrieval techniques for these models and enhancing response generation, particularly for intricate scenarios, ultimately improving the system's practical applicability in dynamic real-world environments.

A fast speed planning algorithm for robotic manipulators

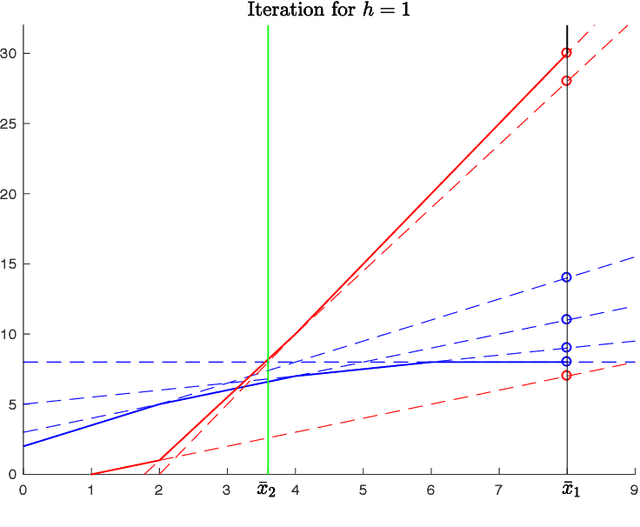
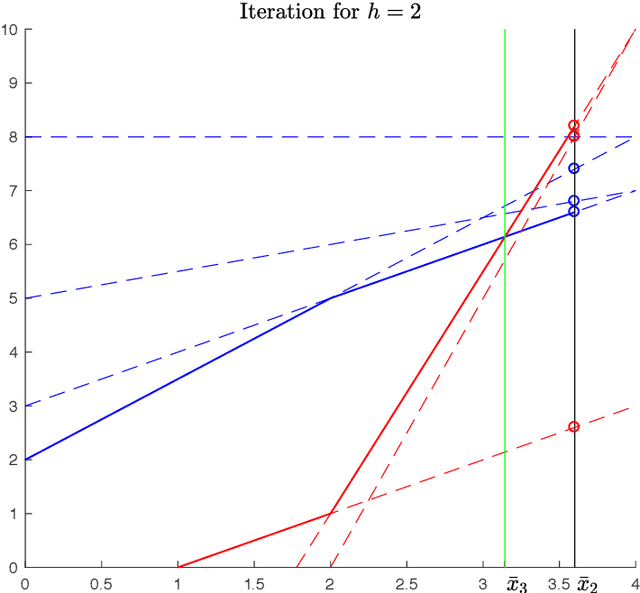
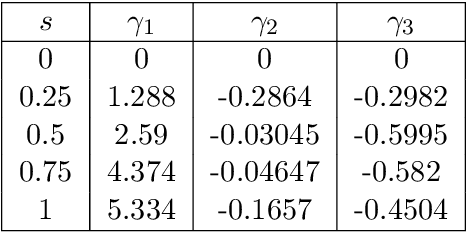
We consider the speed planning problem for a robotic manipulator. In particular, we present an algorithm for finding the time-optimal speed law along an assigned path that satisfies velocity and acceleration constraints and respects the maximum forces and torques allowed by the actuators. The addressed optimization problem is a finite dimensional reformulation of the continuous-time speed optimization problem, obtained by discretizing the speed profile with N points. The proposed algorithm has linear complexity with respect to N and to the number of degrees of freedom. Such complexity is the best possible for this problem. Numerical tests show that the proposed algorithm is significantly faster than algorithms already existing in literature.