An inflationary differential evolution algorithm for space trajectory optimization
Paper and Code
Apr 25, 2011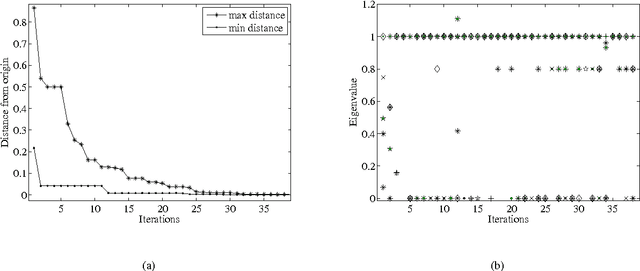
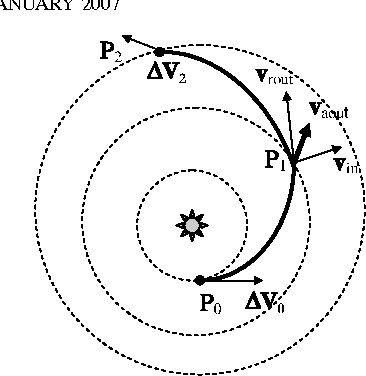
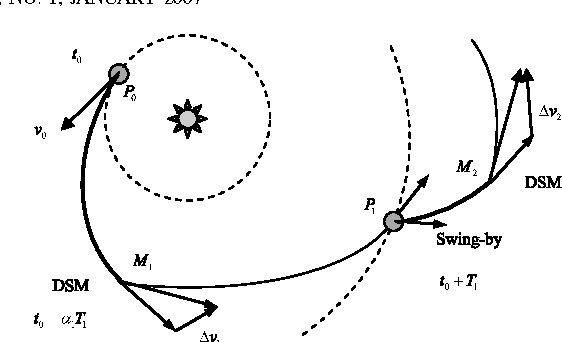
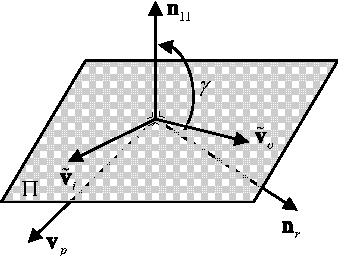
In this paper we define a discrete dynamical system that governs the evolution of a population of agents. From the dynamical system, a variant of Differential Evolution is derived. It is then demonstrated that, under some assumptions on the differential mutation strategy and on the local structure of the objective function, the proposed dynamical system has fixed points towards which it converges with probability one for an infinite number of generations. This property is used to derive an algorithm that performs better than standard Differential Evolution on some space trajectory optimization problems. The novel algorithm is then extended with a guided restart procedure that further increases the performance, reducing the probability of stagnation in deceptive local minima.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge