Invariant Representations with Stochastically Quantized Neural Networks
Paper and Code
Aug 04, 2022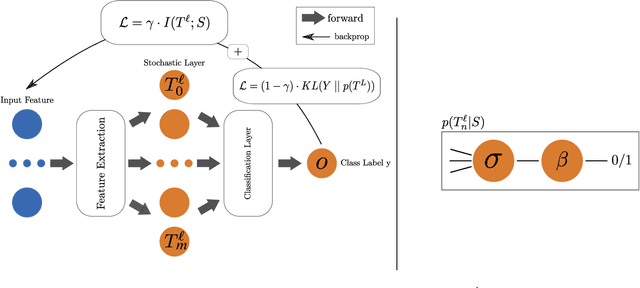
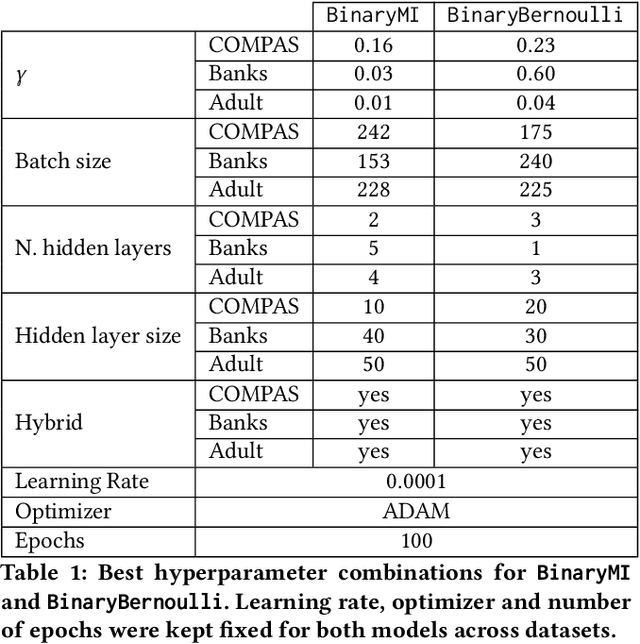
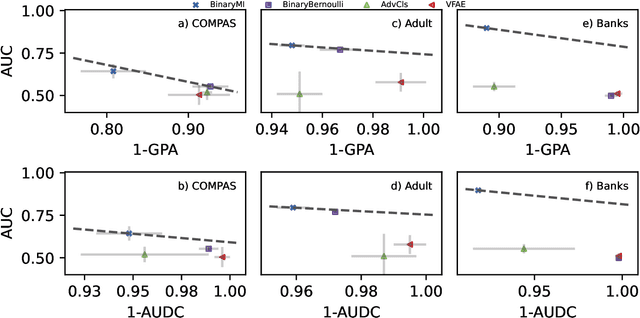

Representation learning algorithms offer the opportunity to learn invariant representations of the input data with regard to nuisance factors. Many authors have leveraged such strategies to learn fair representations, i.e., vectors where information about sensitive attributes is removed. These methods are attractive as they may be interpreted as minimizing the mutual information between a neural layer's activations and a sensitive attribute. However, the theoretical grounding of such methods relies either on the computation of infinitely accurate adversaries or on minimizing a variational upper bound of a mutual information estimate. In this paper, we propose a methodology for direct computation of the mutual information between a neural layer and a sensitive attribute. We employ stochastically-activated binary neural networks, which lets us treat neurons as random variables. We are then able to compute (not bound) the mutual information between a layer and a sensitive attribute and use this information as a regularization factor during gradient descent. We show that this method compares favorably with the state of the art in fair representation learning and that the learned representations display a higher level of invariance compared to full-precision neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge