BitPruning: Learning Bitlengths for Aggressive and Accurate Quantization

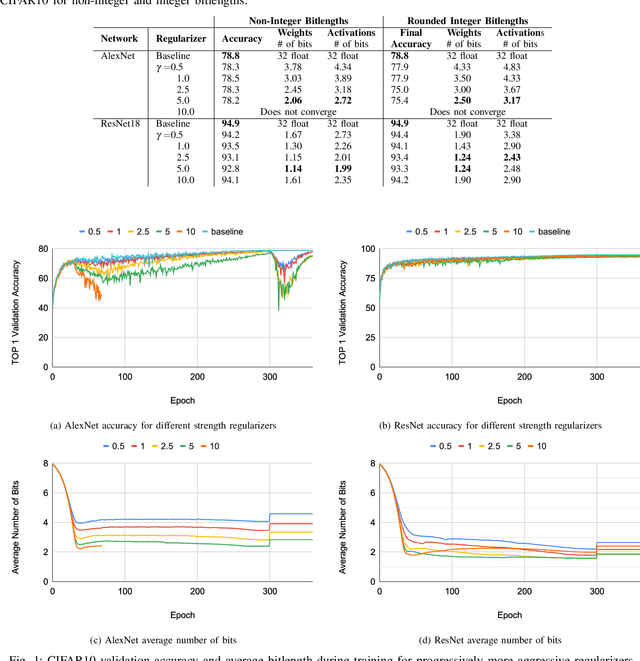
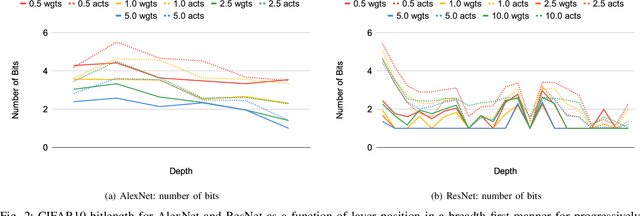
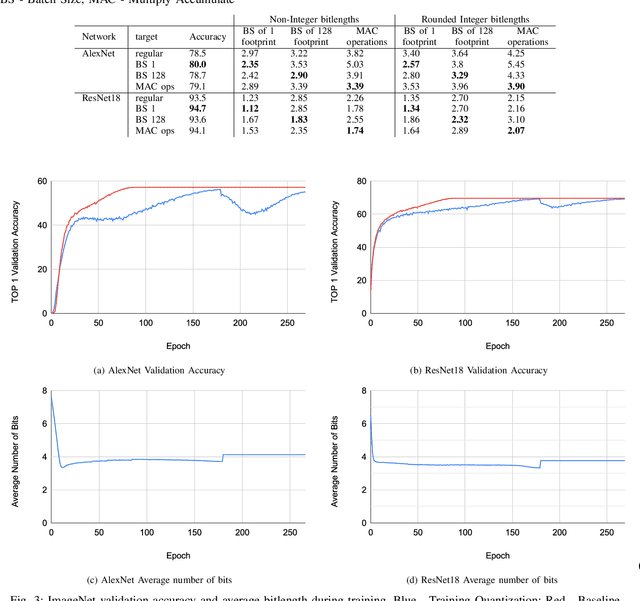
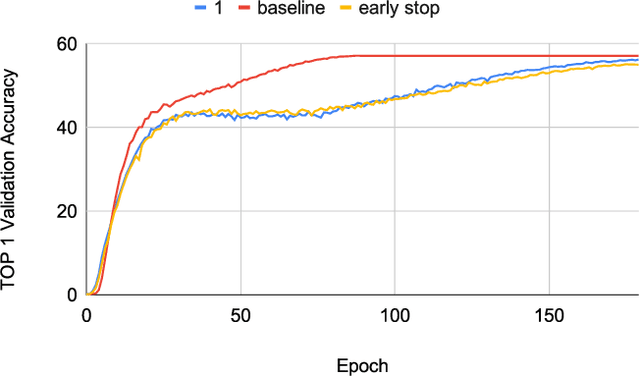
Neural networks have demonstrably achieved state-of-the art accuracy using low-bitlength integer quantization, yielding both execution time and energy benefits on existing hardware designs that support short bitlengths. However, the question of finding the minimum bitlength for a desired accuracy remains open. We introduce a training method for minimizing inference bitlength at any granularity while maintaining accuracy. Furthermore, we propose a regularizer that penalizes large bitlength representations throughout the architecture and show how it can be modified to minimize other quantifiable criteria, such as number of operations or memory footprint. We demonstrate that our method learns thrifty representations while maintaining accuracy. With ImageNet, the method produces an average per layer bitlength of 4.13 and 3.76 bits on AlexNet and ResNet18 respectively, remaining within 2.0% and 0.5% of the baseline TOP-1 accuracy.

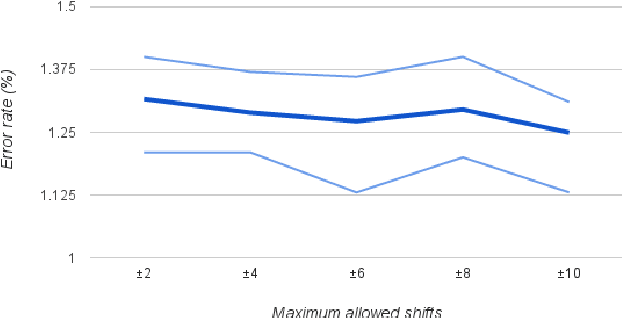
Attention Based Pruning for Shift Networks

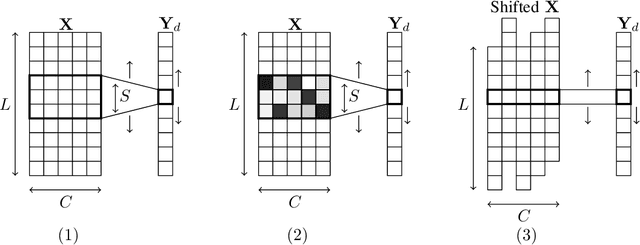
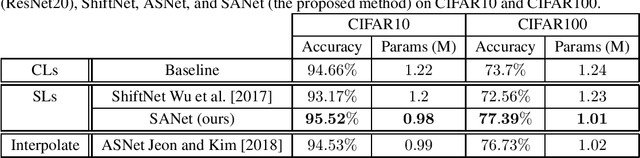
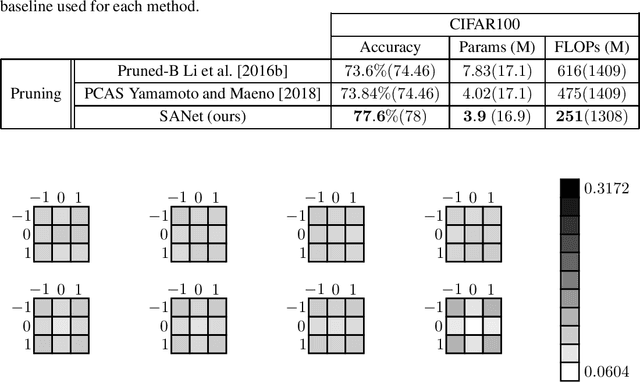
In many application domains such as computer vision, Convolutional Layers (CLs) are key to the accuracy of deep learning methods. However, it is often required to assemble a large number of CLs, each containing thousands of parameters, in order to reach state-of-the-art accuracy, thus resulting in complex and demanding systems that are poorly fitted to resource-limited devices. Recently, methods have been proposed to replace the generic convolution operator by the combination of a shift operation and a simpler 1x1 convolution. The resulting block, called Shift Layer (SL), is an efficient alternative to CLs in the sense it allows to reach similar accuracies on various tasks with faster computations and fewer parameters. In this contribution, we introduce Shift Attention Layers (SALs), which extend SLs by using an attention mechanism that learns which shifts are the best at the same time the network function is trained. We demonstrate SALs are able to outperform vanilla SLs (and CLs) on various object recognition benchmarks while significantly reducing the number of float operations and parameters for the inference.

BNN+: Improved Binary Network Training

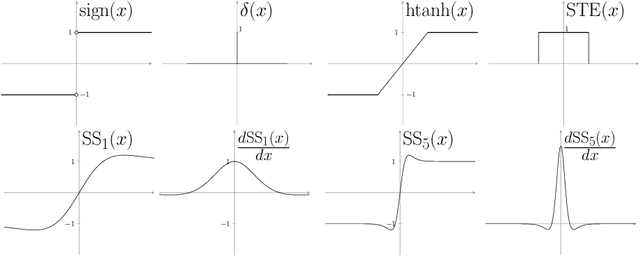
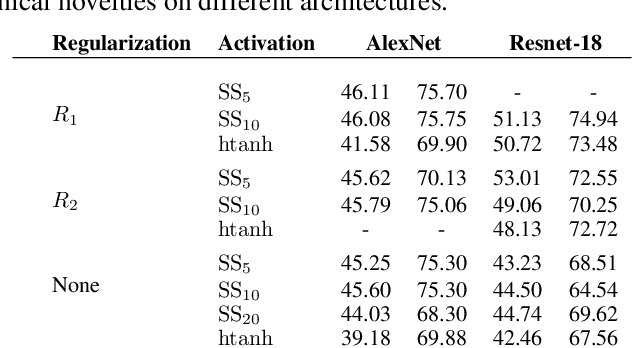
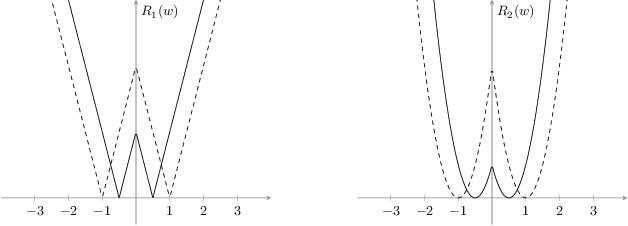
Deep neural networks (DNN) are widely used in many applications. However, their deployment on edge devices has been difficult because they are resource hungry. Binary neural networks (BNN) help to alleviate the prohibitive resource requirements of DNN, where both activations and weights are limited to $1$-bit. We propose an improved binary training method (BNN+), by introducing a regularization function that encourages training weights around binary values. In addition to this, to enhance model performance we add trainable scaling factors to our regularization functions. Furthermore, we use an improved approximation of the derivative of the sign activation function in the backward computation. These additions are based on linear operations that are easily implementable into the binary training framework. We show experimental results on CIFAR-10 obtaining an accuracy of $86.7\%$, on AlexNet and $91.3\%$ with VGG network. On ImageNet, our method also outperforms the traditional BNN method and XNOR-net, using AlexNet by a margin of $4\%$ and $2\%$ top-$1$ accuracy respectively.

Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations

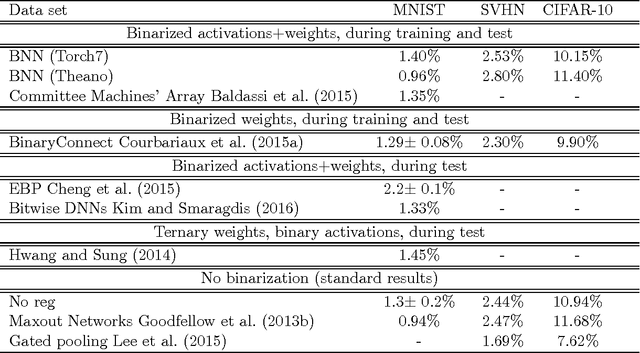
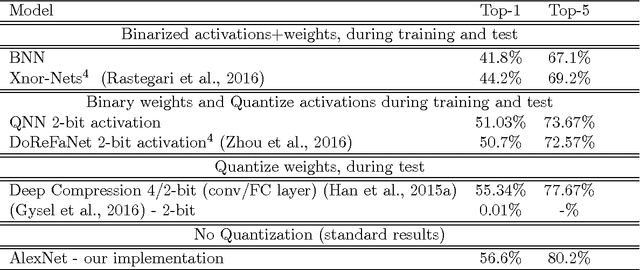
We introduce a method to train Quantized Neural Networks (QNNs) --- neural networks with extremely low precision (e.g., 1-bit) weights and activations, at run-time. At train-time the quantized weights and activations are used for computing the parameter gradients. During the forward pass, QNNs drastically reduce memory size and accesses, and replace most arithmetic operations with bit-wise operations. As a result, power consumption is expected to be drastically reduced. We trained QNNs over the MNIST, CIFAR-10, SVHN and ImageNet datasets. The resulting QNNs achieve prediction accuracy comparable to their 32-bit counterparts. For example, our quantized version of AlexNet with 1-bit weights and 2-bit activations achieves $51\%$ top-1 accuracy. Moreover, we quantize the parameter gradients to 6-bits as well which enables gradients computation using only bit-wise operation. Quantized recurrent neural networks were tested over the Penn Treebank dataset, and achieved comparable accuracy as their 32-bit counterparts using only 4-bits. Last but not least, we programmed a binary matrix multiplication GPU kernel with which it is possible to run our MNIST QNN 7 times faster than with an unoptimized GPU kernel, without suffering any loss in classification accuracy. The QNN code is available online.

BinaryConnect: Training Deep Neural Networks with binary weights during propagations

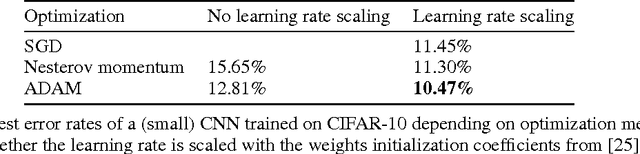
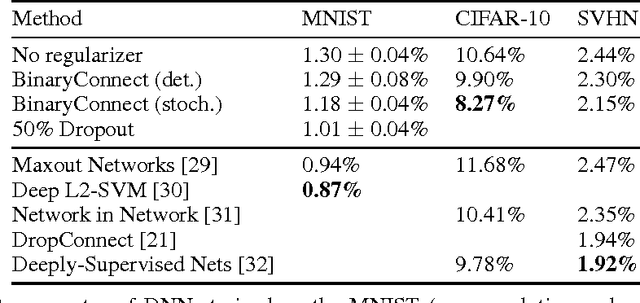
Deep Neural Networks (DNN) have achieved state-of-the-art results in a wide range of tasks, with the best results obtained with large training sets and large models. In the past, GPUs enabled these breakthroughs because of their greater computational speed. In the future, faster computation at both training and test time is likely to be crucial for further progress and for consumer applications on low-power devices. As a result, there is much interest in research and development of dedicated hardware for Deep Learning (DL). Binary weights, i.e., weights which are constrained to only two possible values (e.g. -1 or 1), would bring great benefits to specialized DL hardware by replacing many multiply-accumulate operations by simple accumulations, as multipliers are the most space and power-hungry components of the digital implementation of neural networks. We introduce BinaryConnect, a method which consists in training a DNN with binary weights during the forward and backward propagations, while retaining precision of the stored weights in which gradients are accumulated. Like other dropout schemes, we show that BinaryConnect acts as regularizer and we obtain near state-of-the-art results with BinaryConnect on the permutation-invariant MNIST, CIFAR-10 and SVHN.

Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1

We introduce a method to train Binarized Neural Networks (BNNs) - neural networks with binary weights and activations at run-time. At training-time the binary weights and activations are used for computing the parameters gradients. During the forward pass, BNNs drastically reduce memory size and accesses, and replace most arithmetic operations with bit-wise operations, which is expected to substantially improve power-efficiency. To validate the effectiveness of BNNs we conduct two sets of experiments on the Torch7 and Theano frameworks. On both, BNNs achieved nearly state-of-the-art results over the MNIST, CIFAR-10 and SVHN datasets. Last but not least, we wrote a binary matrix multiplication GPU kernel with which it is possible to run our MNIST BNN 7 times faster than with an unoptimized GPU kernel, without suffering any loss in classification accuracy. The code for training and running our BNNs is available on-line.

Neural Networks with Few Multiplications

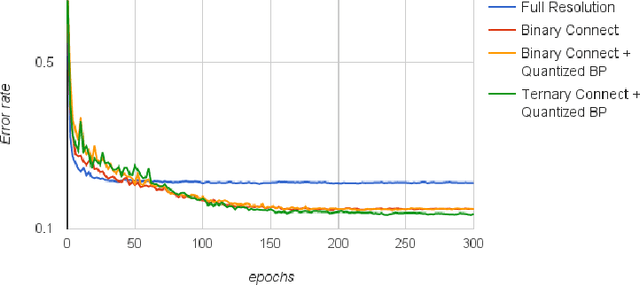
For most deep learning algorithms training is notoriously time consuming. Since most of the computation in training neural networks is typically spent on floating point multiplications, we investigate an approach to training that eliminates the need for most of these. Our method consists of two parts: First we stochastically binarize weights to convert multiplications involved in computing hidden states to sign changes. Second, while back-propagating error derivatives, in addition to binarizing the weights, we quantize the representations at each layer to convert the remaining multiplications into binary shifts. Experimental results across 3 popular datasets (MNIST, CIFAR10, SVHN) show that this approach not only does not hurt classification performance but can result in even better performance than standard stochastic gradient descent training, paving the way to fast, hardware-friendly training of neural networks.

Training deep neural networks with low precision multiplications

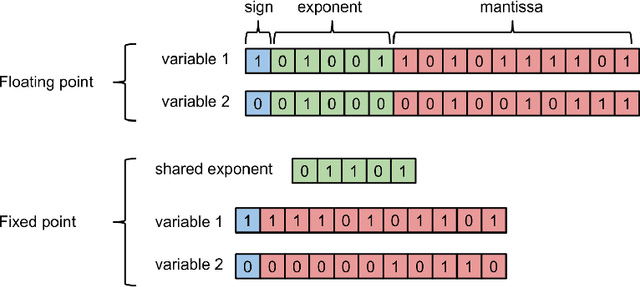
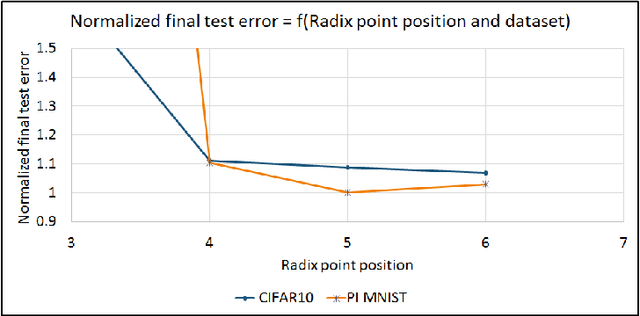
Multipliers are the most space and power-hungry arithmetic operators of the digital implementation of deep neural networks. We train a set of state-of-the-art neural networks (Maxout networks) on three benchmark datasets: MNIST, CIFAR-10 and SVHN. They are trained with three distinct formats: floating point, fixed point and dynamic fixed point. For each of those datasets and for each of those formats, we assess the impact of the precision of the multiplications on the final error after training. We find that very low precision is sufficient not just for running trained networks but also for training them. For example, it is possible to train Maxout networks with 10 bits multiplications.