QGen: On the Ability to Generalize in Quantization Aware Training

Quantization lowers memory usage, computational requirements, and latency by utilizing fewer bits to represent model weights and activations. In this work, we investigate the generalization properties of quantized neural networks, a characteristic that has received little attention despite its implications on model performance. In particular, first, we develop a theoretical model for quantization in neural networks and demonstrate how quantization functions as a form of regularization. Second, motivated by recent work connecting the sharpness of the loss landscape and generalization, we derive an approximate bound for the generalization of quantized models conditioned on the amount of quantization noise. We then validate our hypothesis by experimenting with over 2000 models trained on CIFAR-10, CIFAR-100, and ImageNet datasets on convolutional and transformer-based models.

QReg: On Regularization Effects of Quantization

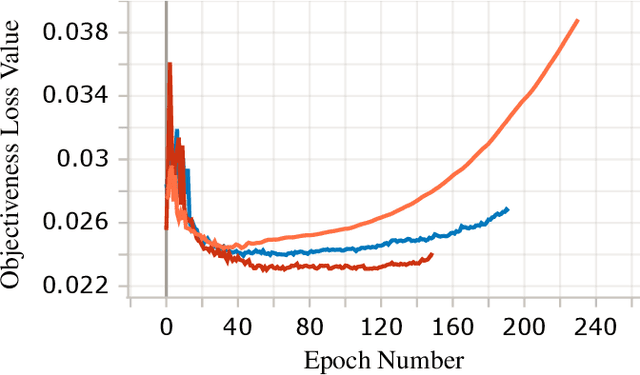
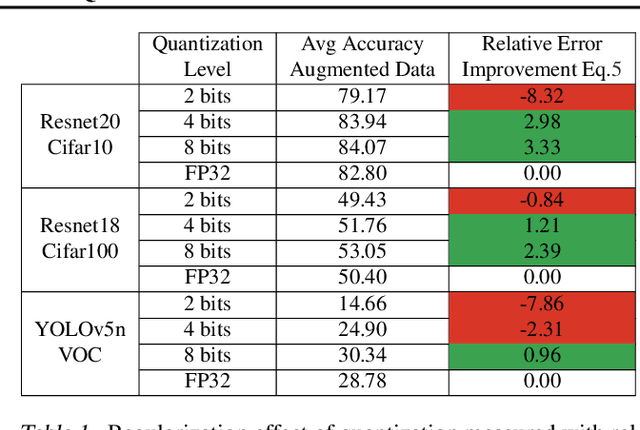
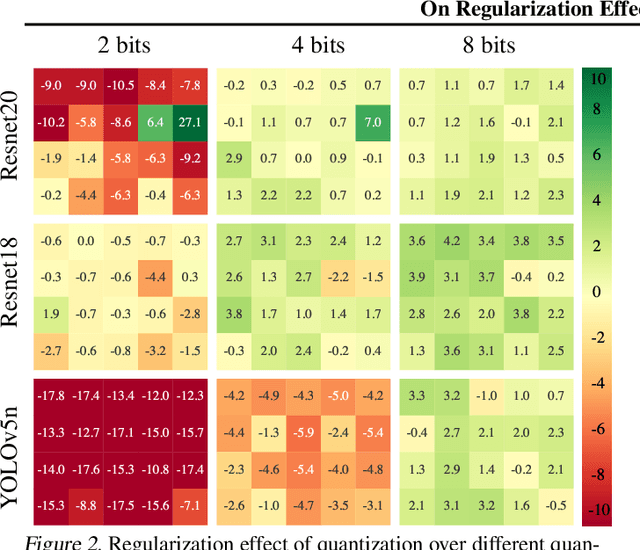
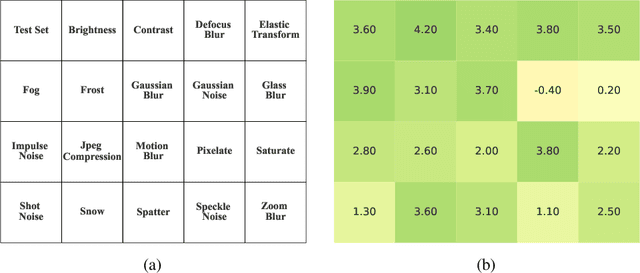
In this paper we study the effects of quantization in DNN training. We hypothesize that weight quantization is a form of regularization and the amount of regularization is correlated with the quantization level (precision). We confirm our hypothesis by providing analytical study and empirical results. By modeling weight quantization as a form of additive noise to weights, we explore how this noise propagates through the network at training time. We then show that the magnitude of this noise is correlated with the level of quantization. To confirm our analytical study, we performed an extensive list of experiments summarized in this paper in which we show that the regularization effects of quantization can be seen in various vision tasks and models, over various datasets. Based on our study, we propose that 8-bit quantization provides a reliable form of regularization in different vision tasks and models.

U-Net Fixed-Point Quantization for Medical Image Segmentation

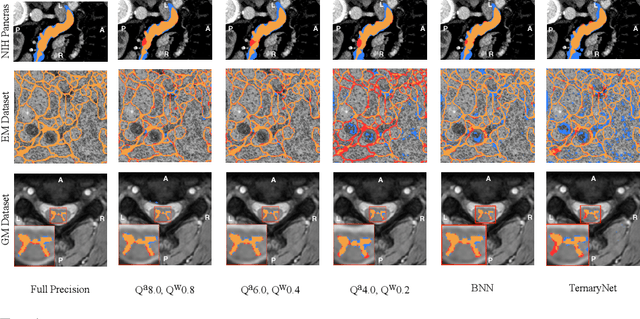
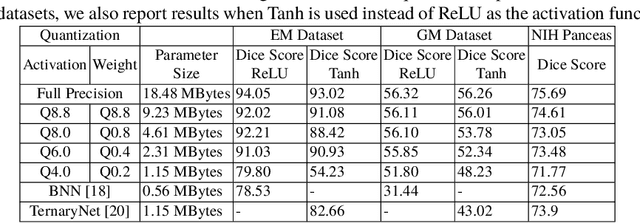
Model quantization is leveraged to reduce the memory consumption and the computation time of deep neural networks. This is achieved by representing weights and activations with a lower bit resolution when compared to their high precision floating point counterparts. The suitable level of quantization is directly related to the model performance. Lowering the quantization precision (e.g. 2 bits), reduces the amount of memory required to store model parameters and the amount of logic required to implement computational blocks, which contributes to reducing the power consumption of the entire system. These benefits typically come at the cost of reduced accuracy. The main challenge is to quantize a network as much as possible, while maintaining the performance accuracy. In this work, we present a quantization method for the U-Net architecture, a popular model in medical image segmentation. We then apply our quantization algorithm to three datasets: (1) the Spinal Cord Gray Matter Segmentation (GM), (2) the ISBI challenge for segmentation of neuronal structures in Electron Microscopic (EM), and (3) the public National Institute of Health (NIH) dataset for pancreas segmentation in abdominal CT scans. The reported results demonstrate that with only 4 bits for weights and 6 bits for activations, we obtain 8 fold reduction in memory requirements while loosing only 2.21%, 0.57% and 2.09% dice overlap score for EM, GM and NIH datasets respectively. Our fixed point quantization provides a flexible trade off between accuracy and memory requirement which is not provided by previous quantization methods for U-Net such as TernaryNet.

BinaryConnect: Training Deep Neural Networks with binary weights during propagations

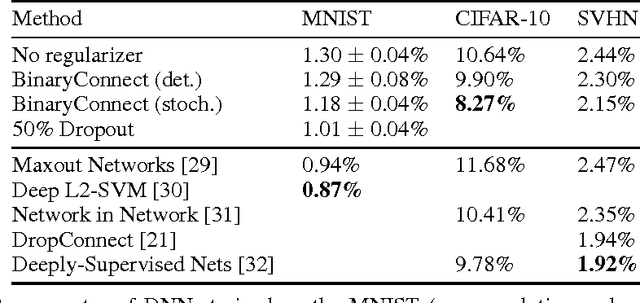
Deep Neural Networks (DNN) have achieved state-of-the-art results in a wide range of tasks, with the best results obtained with large training sets and large models. In the past, GPUs enabled these breakthroughs because of their greater computational speed. In the future, faster computation at both training and test time is likely to be crucial for further progress and for consumer applications on low-power devices. As a result, there is much interest in research and development of dedicated hardware for Deep Learning (DL). Binary weights, i.e., weights which are constrained to only two possible values (e.g. -1 or 1), would bring great benefits to specialized DL hardware by replacing many multiply-accumulate operations by simple accumulations, as multipliers are the most space and power-hungry components of the digital implementation of neural networks. We introduce BinaryConnect, a method which consists in training a DNN with binary weights during the forward and backward propagations, while retaining precision of the stored weights in which gradients are accumulated. Like other dropout schemes, we show that BinaryConnect acts as regularizer and we obtain near state-of-the-art results with BinaryConnect on the permutation-invariant MNIST, CIFAR-10 and SVHN.

Training deep neural networks with low precision multiplications

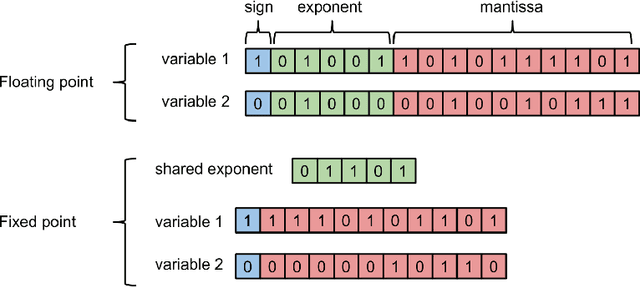
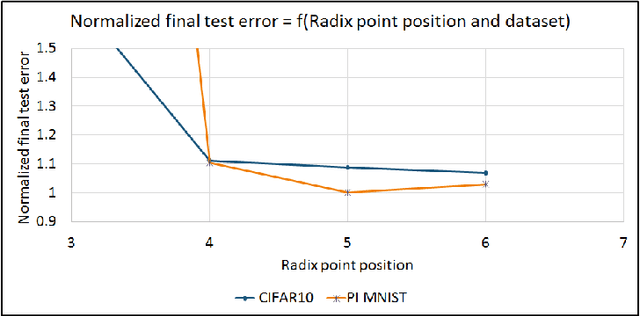
Multipliers are the most space and power-hungry arithmetic operators of the digital implementation of deep neural networks. We train a set of state-of-the-art neural networks (Maxout networks) on three benchmark datasets: MNIST, CIFAR-10 and SVHN. They are trained with three distinct formats: floating point, fixed point and dynamic fixed point. For each of those datasets and for each of those formats, we assess the impact of the precision of the multiplications on the final error after training. We find that very low precision is sufficient not just for running trained networks but also for training them. For example, it is possible to train Maxout networks with 10 bits multiplications.