Coarse Graining of Data via Inhomogeneous Diffusion Condensation

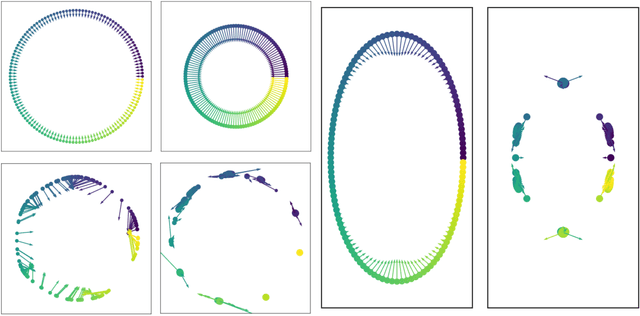
Big data often has emergent structure that exists at multiple levels of abstraction, which are useful for characterizing complex interactions and dynamics of the observations. Here, we consider multiple levels of abstraction via a multiresolution geometry of data points at different granularities. To construct this geometry we define a time-inhomogeneous diffusion process that effectively condenses data points together to uncover nested groupings at larger and larger granularities. This inhomogeneous process creates a deep cascade of intrinsic low pass filters in the data that are applied in sequence to gradually eliminate local variability while adjusting the learned data geometry to increasingly coarser resolutions. We provide visualizations to exhibit our method as a "continuously-hierarchical" clustering with directions of eliminated variation highlighted at each step. The utility of our algorithm is demonstrated via neuronal data condensation, where the constructed multiresolution data geometry uncovers the organization, grouping, and connectivity between neurons.

Kymatio: Scattering Transforms in Python

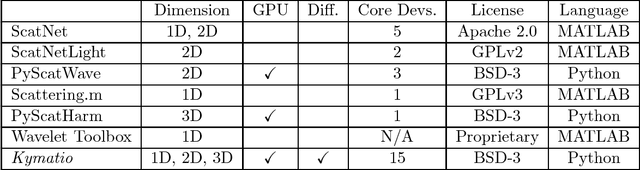
The wavelet scattering transform is an invariant signal representation suitable for many signal processing and machine learning applications. We present the Kymatio software package, an easy-to-use, high-performance Python implementation of the scattering transform in 1D, 2D, and 3D that is compatible with modern deep learning frameworks. All transforms may be executed on a GPU (in addition to CPU), offering a considerable speed up over CPU implementations. The package also has a small memory footprint, resulting inefficient memory usage. The source code, documentation, and examples are available undera BSD license at https://www.kymat.io/