Soft Measures for Extracting Causal Collective Intelligence

Understanding and modeling collective intelligence is essential for addressing complex social systems. Directed graphs called fuzzy cognitive maps (FCMs) offer a powerful tool for encoding causal mental models, but extracting high-integrity FCMs from text is challenging. This study presents an approach using large language models (LLMs) to automate FCM extraction. We introduce novel graph-based similarity measures and evaluate them by correlating their outputs with human judgments through the Elo rating system. Results show positive correlations with human evaluations, but even the best-performing measure exhibits limitations in capturing FCM nuances. Fine-tuning LLMs improves performance, but existing measures still fall short. This study highlights the need for soft similarity measures tailored to FCM extraction, advancing collective intelligence modeling with NLP.

MagNet: A Magnetic Neural Network for Directed Graphs

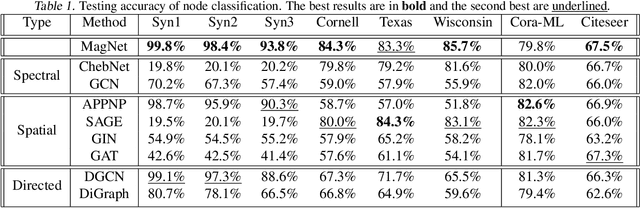
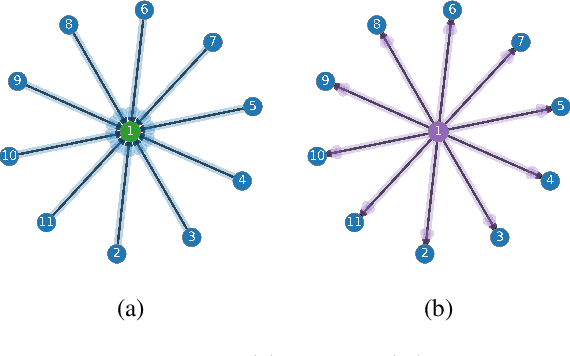
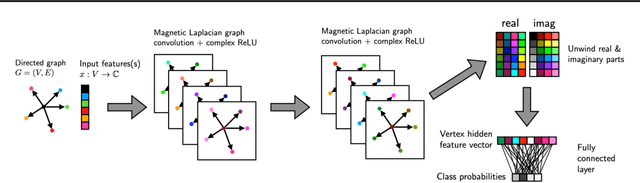
The prevalence of graph-based data has spurred the rapid development of graph neural networks (GNNs) and related machine learning algorithms. Yet, despite the many data sets naturally modeled as directed graphs, including citation, website, and traffic networks, the vast majority of this research focuses on undirected graphs. In this paper, we propose MagNet, a spectral GNN for directed graphs based on a complex Hermitian matrix known as the magnetic Laplacian. This matrix encodes undirected geometric structure in the magnitude of its entries and directional information in the phase of its entries. A "charge" parameter attunes spectral information to variation among directed cycles. We show that MagNet's performance exceeds other spectral GNNs on directed graph node classification and link prediction tasks for a variety of datasets and exceeds commonly used spatial GNNs on a majority of such. The underlying principles of MagNet are such that it can be adapted to other spectral GNN architectures.

Coarse Graining of Data via Inhomogeneous Diffusion Condensation

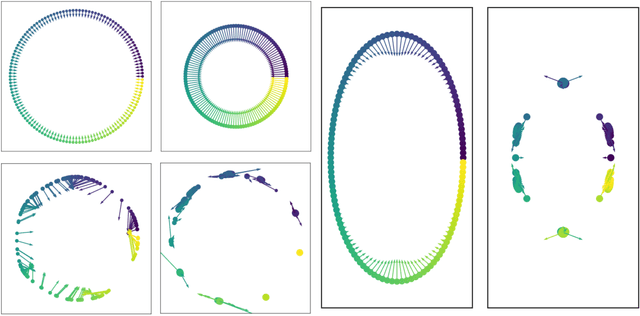
Big data often has emergent structure that exists at multiple levels of abstraction, which are useful for characterizing complex interactions and dynamics of the observations. Here, we consider multiple levels of abstraction via a multiresolution geometry of data points at different granularities. To construct this geometry we define a time-inhomogeneous diffusion process that effectively condenses data points together to uncover nested groupings at larger and larger granularities. This inhomogeneous process creates a deep cascade of intrinsic low pass filters in the data that are applied in sequence to gradually eliminate local variability while adjusting the learned data geometry to increasingly coarser resolutions. We provide visualizations to exhibit our method as a "continuously-hierarchical" clustering with directions of eliminated variation highlighted at each step. The utility of our algorithm is demonstrated via neuronal data condensation, where the constructed multiresolution data geometry uncovers the organization, grouping, and connectivity between neurons.