MagNet: A Magnetic Neural Network for Directed Graphs

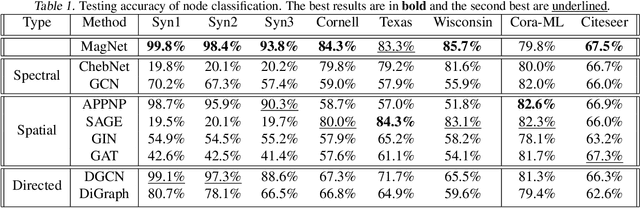
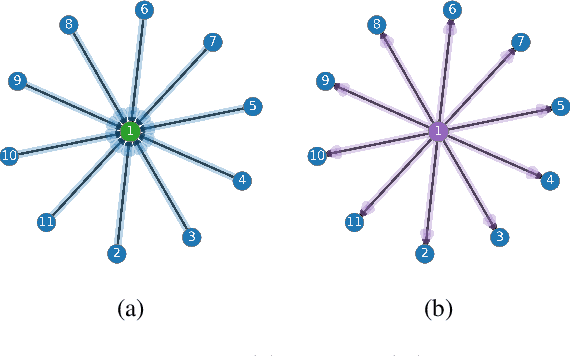
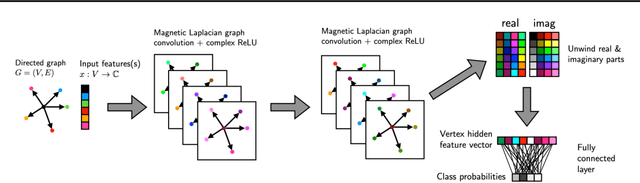
The prevalence of graph-based data has spurred the rapid development of graph neural networks (GNNs) and related machine learning algorithms. Yet, despite the many data sets naturally modeled as directed graphs, including citation, website, and traffic networks, the vast majority of this research focuses on undirected graphs. In this paper, we propose MagNet, a spectral GNN for directed graphs based on a complex Hermitian matrix known as the magnetic Laplacian. This matrix encodes undirected geometric structure in the magnitude of its entries and directional information in the phase of its entries. A "charge" parameter attunes spectral information to variation among directed cycles. We show that MagNet's performance exceeds other spectral GNNs on directed graph node classification and link prediction tasks for a variety of datasets and exceeds commonly used spatial GNNs on a majority of such. The underlying principles of MagNet are such that it can be adapted to other spectral GNN architectures.