Verbalized Algorithms

Instead of querying LLMs in a one-shot manner and hoping to get the right answer for a reasoning task, we propose a paradigm we call \emph{verbalized algorithms} (VAs), which leverage classical algorithms with established theoretical understanding. VAs decompose a task into simple elementary operations on natural language strings that they should be able to answer reliably, and limit the scope of LLMs to only those simple tasks. For example, for sorting a series of natural language strings, \emph{verbalized sorting} uses an LLM as a binary comparison oracle in a known and well-analyzed sorting algorithm (e.g., bitonic sorting network). We demonstrate the effectiveness of this approach on sorting and clustering tasks.

Bilevel MCTS for Amortized O(1) Node Selection in Classical Planning

We study an efficient implementation of Multi-Armed Bandit (MAB)-based Monte-Carlo Tree Search (MCTS) for classical planning. One weakness of MCTS is that it spends a significant time deciding which node to expand next. While selecting a node from an OPEN list with $N$ nodes has $O(1)$ runtime complexity with traditional array-based priority-queues for dense integer keys, the tree-based OPEN list used by MCTS requires $O(\log N)$, which roughly corresponds to the search depth $d$. In classical planning, $d$ is arbitrarily large (e.g., $2^k-1$ in $k$-disk Tower-of-Hanoi) and the runtime for node selection is significant, unlike in game tree search, where the cost is negligible compared to the node evaluation (rollouts) because $d$ is inherently limited by the game (e.g., $d\leq 361$ in Go). To improve this bottleneck, we propose a bilevel modification to MCTS that runs a best-first search from each selected leaf node with an expansion budget proportional to $d$, which achieves amortized $O(1)$ runtime for node selection, equivalent to the traditional queue-based OPEN list. In addition, we introduce Tree Collapsing, an enhancement that reduces action selection steps and further improves the performance.

"Don't Do That!": Guiding Embodied Systems through Large Language Model-based Constraint Generation

Recent advancements in large language models (LLMs) have spurred interest in robotic navigation that incorporates complex spatial, mathematical, and conditional constraints from natural language into the planning problem. Such constraints can be informal yet highly complex, making it challenging to translate into a formal description that can be passed on to a planning algorithm. In this paper, we propose STPR, a constraint generation framework that uses LLMs to translate constraints (expressed as instructions on ``what not to do'') into executable Python functions. STPR leverages the LLM's strong coding capabilities to shift the problem description from language into structured and transparent code, thus circumventing complex reasoning and avoiding potential hallucinations. We show that these LLM-generated functions accurately describe even complex mathematical constraints, and apply them to point cloud representations with traditional search algorithms. Experiments in a simulated Gazebo environment show that STPR ensures full compliance across several constraints and scenarios, while having short runtimes. We also verify that STPR can be used with smaller, code-specific LLMs, making it applicable to a wide range of compact models at low inference cost.

Extreme Value Monte Carlo Tree Search

Despite being successful in board games and reinforcement learning (RL), UCT, a Monte-Carlo Tree Search (MCTS) combined with UCB1 Multi-Armed Bandit (MAB), has had limited success in domain-independent planning until recently. Previous work showed that UCB1, designed for $[0,1]$-bounded rewards, is not appropriate for estimating the distance-to-go which are potentially unbounded in $\mathbb{R}$, such as heuristic functions used in classical planning, then proposed combining MCTS with MABs designed for Gaussian reward distributions and successfully improved the performance. In this paper, we further sharpen our understanding of ideal bandits for planning tasks. Existing work has two issues: First, while Gaussian MABs no longer over-specify the distances as $h\in [0,1]$, they under-specify them as $h\in [-\infty,\infty]$ while they are non-negative and can be further bounded in some cases. Second, there is no theoretical justifications for Full-Bellman backup (Schulte & Keller, 2014) that backpropagates minimum/maximum of samples. We identified \emph{extreme value} statistics as a theoretical framework that resolves both issues at once and propose two bandits, UCB1-Uniform/Power, and apply them to MCTS for classical planning. We formally prove their regret bounds and empirically demonstrate their performance in classical planning.

Utilizing Admissible Bounds for Heuristic Learning

While learning a heuristic function for forward search algorithms with modern machine learning techniques has been gaining interest in recent years, there has been little theoretical understanding of \emph{what} they should learn, \emph{how} to train them, and \emph{why} we do so. This lack of understanding leads to various literature performing an ad-hoc selection of datasets (suboptimal vs optimal costs or admissible vs inadmissible heuristics) and optimization metrics (e.g., squared vs absolute errors). Moreover, due to the lack of admissibility of the resulting trained heuristics, little focus has been put on the role of admissibility \emph{during} learning. This paper articulates the role of admissible heuristics in supervised heuristic learning using them as parameters of Truncated Gaussian distributions, which tightens the hypothesis space compared to ordinary Gaussian distributions. We argue that this mathematical model faithfully follows the principle of maximum entropy and empirically show that, as a result, it yields more accurate heuristics and converges faster during training.

Scale-Adaptive Balancing of Exploration and Exploitation in Classical Planning

Balancing exploration and exploitation has been an important problem in both game tree search and automated planning. However, while the problem has been extensively analyzed within the Multi-Armed Bandit (MAB) literature, the planning community has had limited success when attempting to apply those results. We show that a more detailed theoretical understanding of MAB literature helps improve existing planning algorithms that are based on Monte Carlo Tree Search (MCTS) / Trial Based Heuristic Tree Search (THTS). In particular, THTS uses UCB1 MAB algorithms in an ad hoc manner, as UCB1's theoretical requirement of fixed bounded support reward distributions is not satisfied within heuristic search for classical planning. The core issue lies in UCB1's lack of adaptations to the different scales of the rewards. We propose GreedyUCT-Normal, a MCTS/THTS algorithm with UCB1-Normal bandit for agile classical planning, which handles distributions with different scales by taking the reward variance into consideration, and resulted in an improved algorithmic performance (more plans found with less node expansions) that outperforms Greedy Best First Search and existing MCTS/THTS-based algorithms (GreedyUCT,GreedyUCT*).

Analytical Conjugate Priors for Subclasses of Generalized Pareto Distributions

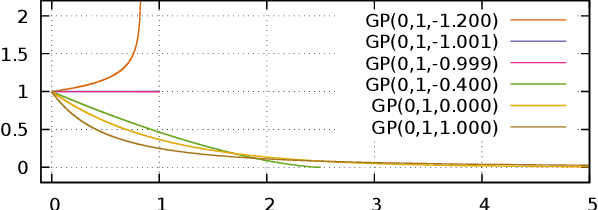
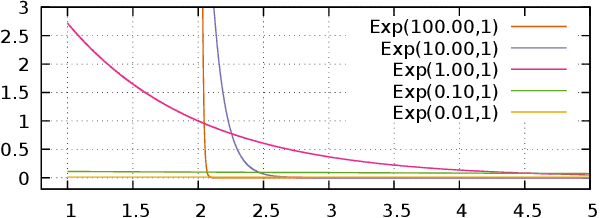
This article is written for pedagogical purposes aiming at practitioners trying to estimate the finite support of continuous probability distributions, i.e., the minimum and the maximum of a distribution defined on a finite domain. Generalized Pareto distribution GP({\theta}, {\sigma}, {\xi}) is a three-parameter distribution which plays a key role in Peaks-Over-Threshold framework for tail estimation in Extreme Value Theory. Estimators for GP often lack analytical solutions and the best known Bayesian methods for GP involves numerical methods. Moreover, existing literature focuses on estimating the scale {\sigma} and the shape {\xi}, lacking discussion of the estimation of the location {\theta} which is the lower support of (minimum value possible in) a GP. To fill the gap, we analyze four two-parameter subclasses of GP whose conjugate priors can be obtained analytically, although some of the results are known. Namely, we prove the conjugacy for {\xi} > 0 (Pareto), {\xi} = 0 (Shifted Exponential), {\xi} < 0 (Power), and {\xi} = -1 (Two-parameter Uniform).

Dr. Neurosymbolic, or: How I Learned to Stop Worrying and Accept Statistics

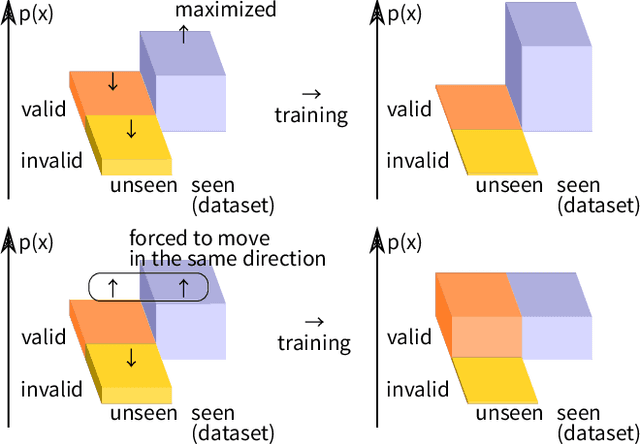
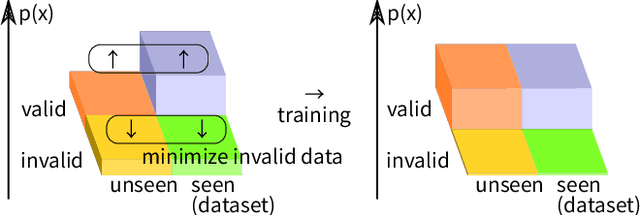
The symbolic AI community is increasingly trying to embrace machine learning in neuro-symbolic architectures, yet is still struggling due to cultural barriers. To break the barrier, this rather opinionated personal memo attempts to explain and rectify the conventions in Statistics, Machine Learning, and Deep Learning from the viewpoint of outsiders. It provides a step-by-step protocol for designing a machine learning system that satisfies a minimum theoretical guarantee necessary for being taken seriously by the symbolic AI community, i.e., it discusses "in what condition we can stop worrying and accept statistical machine learning." Some highlights: Most textbooks are written for those who plan to specialize in Stat/ML/DL and are supposed to accept jargons. This memo is for experienced symbolic researchers that hear a lot of buzz but are still uncertain and skeptical. Information on Stat/ML/DL is currently too scattered or too noisy to invest in. This memo prioritizes compactness and pays special attention to concepts that resonate well with symbolic paradigms. I hope this memo offers time savings. It prioritizes general mathematical modeling and does not discuss any specific function approximator, such as neural networks (NNs), SVMs, decision trees, etc. It is open to corrections. Consider this memo as something similar to a blog post taking the form of a paper on Arxiv.

Width-Based Planning and Active Learning for Atari

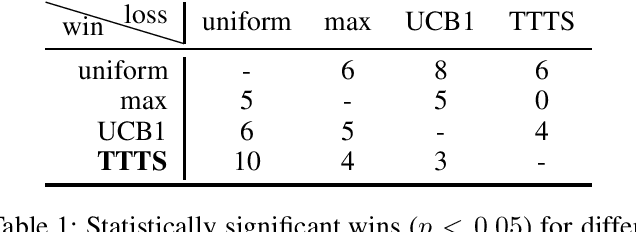
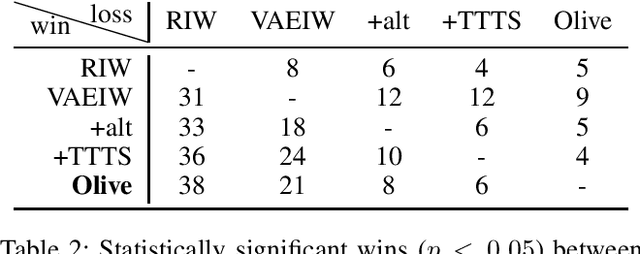
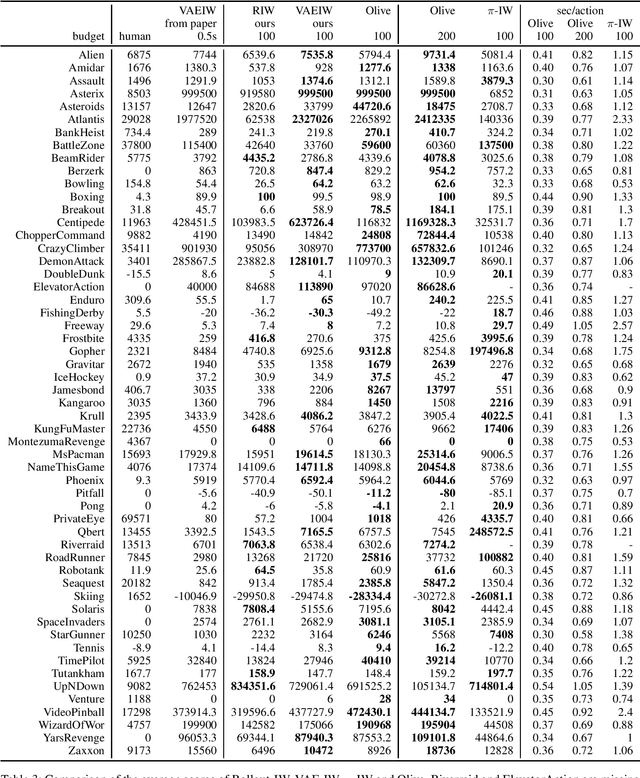
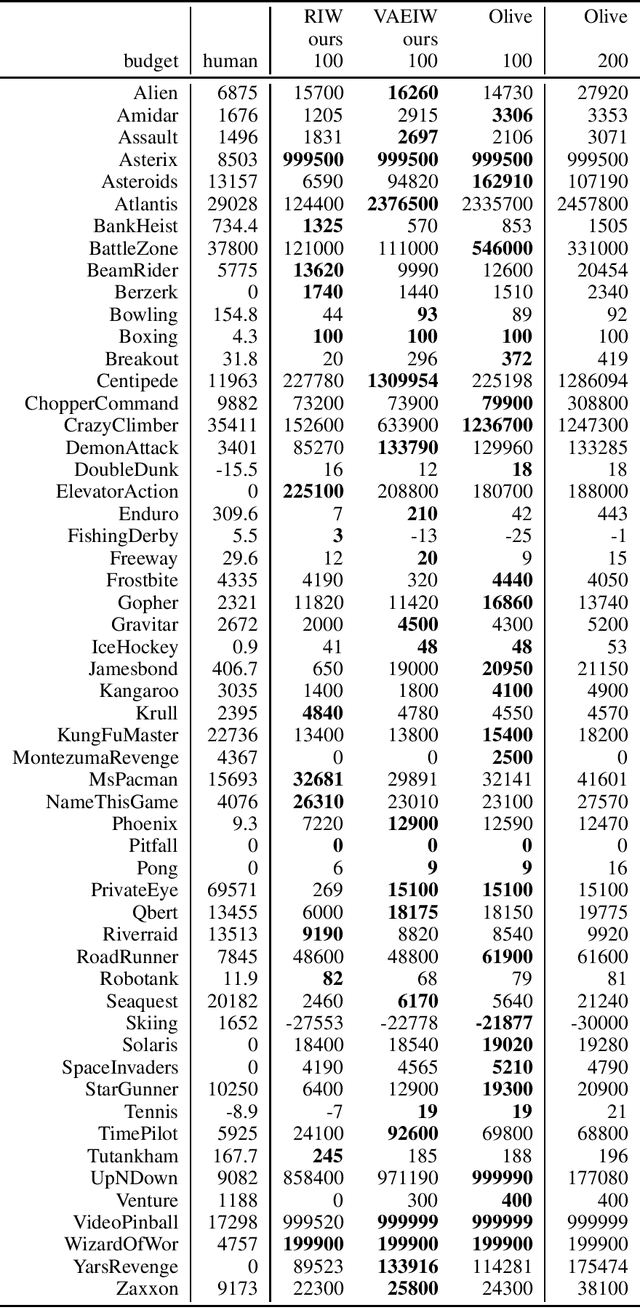
Width-based planning has shown promising results on Atari 2600 games using pixel input, while using substantially fewer environment interactions than reinforcement learning. Recent width-based approaches have computed feature vectors for each screen using a hand designed feature set or a variational autoencoder (VAE) trained on game screens, and prune screens that do not have novel features during the search. In this paper, we explore consideration of uncertainty in features generated by a VAE during width-based planning. Our primary contribution is the introduction of active learning to maximize the utility of screens observed during planning. Experimental results demonstrate that use of active learning strategies increases gameplay scores compared to alternative width-based approaches with equal numbers of environment interactions.

Reinforcement Learning for Classical Planning: Viewing Heuristics as Dense Reward Generators

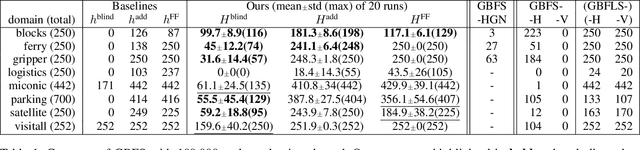
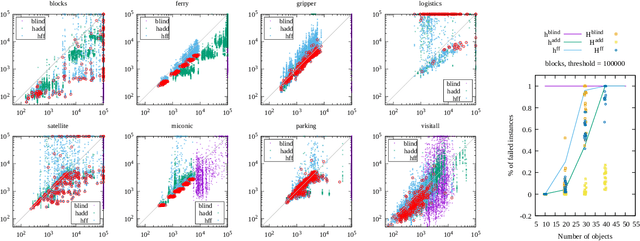
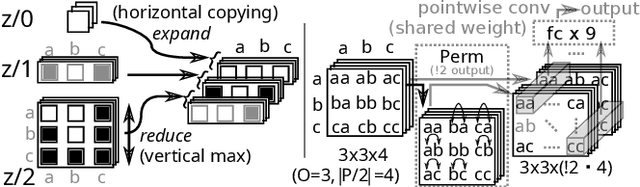
Recent advances in reinforcement learning (RL) have led to a growing interest in applying RL to classical planning domains or applying classical planning methods to some complex RL domains. However, the long-horizon goal-based problems found in classical planning lead to sparse rewards for RL, making direct application inefficient. In this paper, we propose to leverage domain-independent heuristic functions commonly used in the classical planning literature to improve the sample efficiency of RL. These classical heuristics act as dense reward generators to alleviate the sparse-rewards issue and enable our RL agent to learn domain-specific value functions as residuals on these heuristics, making learning easier. Correct application of this technique requires consolidating the discounted metric used in RL and the non-discounted metric used in heuristics. We implement the value functions using Neural Logic Machines, a neural network architecture designed for grounded first-order logic inputs. We demonstrate on several classical planning domains that using classical heuristics for RL allows for good sample efficiency compared to sparse-reward RL. We further show that our learned value functions generalize to novel problem instances in the same domain.