Analytical Conjugate Priors for Subclasses of Generalized Pareto Distributions
Paper and Code
Mar 21, 2023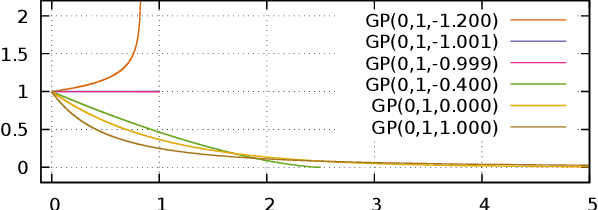


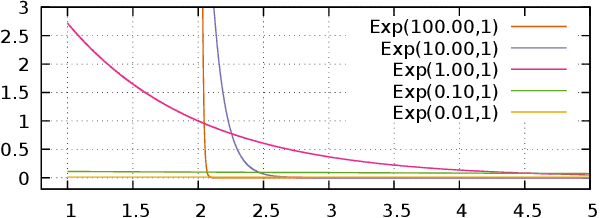
This article is written for pedagogical purposes aiming at practitioners trying to estimate the finite support of continuous probability distributions, i.e., the minimum and the maximum of a distribution defined on a finite domain. Generalized Pareto distribution GP({\theta}, {\sigma}, {\xi}) is a three-parameter distribution which plays a key role in Peaks-Over-Threshold framework for tail estimation in Extreme Value Theory. Estimators for GP often lack analytical solutions and the best known Bayesian methods for GP involves numerical methods. Moreover, existing literature focuses on estimating the scale {\sigma} and the shape {\xi}, lacking discussion of the estimation of the location {\theta} which is the lower support of (minimum value possible in) a GP. To fill the gap, we analyze four two-parameter subclasses of GP whose conjugate priors can be obtained analytically, although some of the results are known. Namely, we prove the conjugacy for {\xi} > 0 (Pareto), {\xi} = 0 (Shifted Exponential), {\xi} < 0 (Power), and {\xi} = -1 (Two-parameter Uniform).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge