Discrete Word Embedding for Logical Natural Language Understanding

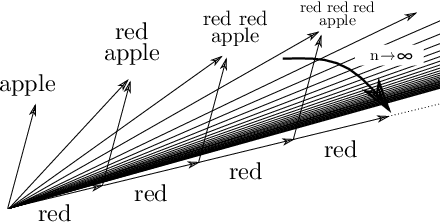
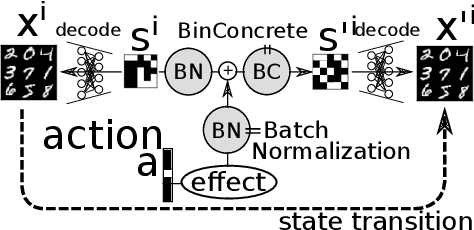
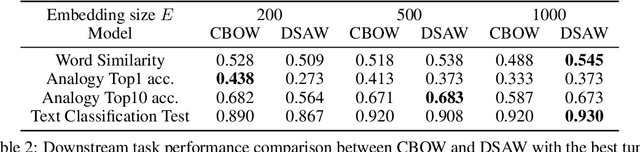
In this paper, we propose an unsupervised neural model for learning a discrete embedding of words. While being discrete, our embedding supports vector arithmetic operations similar to continuous embeddings by interpreting each word as a set of propositional statements describing a rule. The formulation of our vector arithmetic closely reflects the logical structure originating from the symbolic sequential decision making formalism (classical/STRIPS planning). Contrary to the conventional wisdom that discrete representation cannot perform well due to the lack of ability to capture the uncertainty, our representation is competitive against the continuous representations in several downstream tasks. We demonstrate that our embedding is directly compatible with the symbolic, classical planning solvers by performing a "paraphrasing" task. Due to the discrete/logical decision making in classical algorithms with deterministic (non-probabilistic) completeness, and also because it does not require additional training on the paraphrasing dataset, our system can negatively answer a paraphrasing query (inexistence of solutions), and can answer that only some approximate solutions exist -- A feature that is missing in the recent, huge, purely neural language models such as GPT-3.