TopoX: A Suite of Python Packages for Machine Learning on Topological Domains

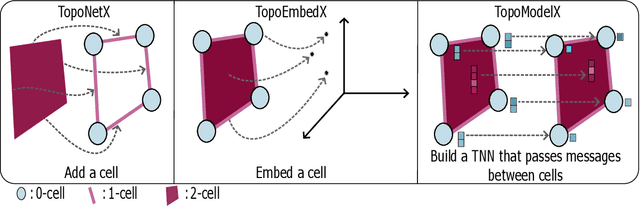
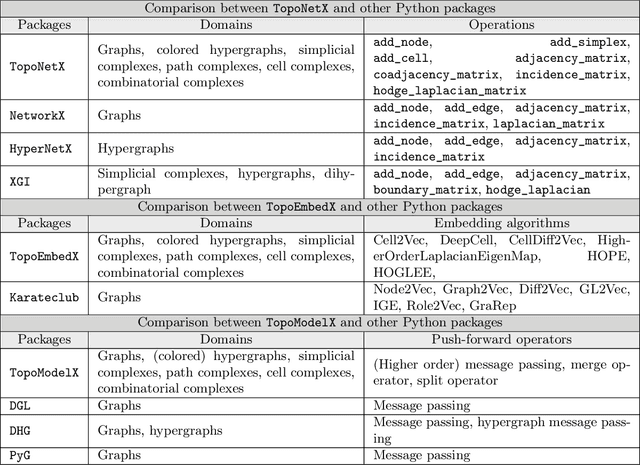
We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.

Hodge-Compositional Edge Gaussian Processes

We propose principled Gaussian processes (GPs) for modeling functions defined over the edge set of a simplicial 2-complex, a structure similar to a graph in which edges may form triangular faces. This approach is intended for learning flow-type data on networks where edge flows can be characterized by the discrete divergence and curl. Drawing upon the Hodge decomposition, we first develop classes of divergence-free and curl-free edge GPs, suitable for various applications. We then combine them to create \emph{Hodge-compositional edge GPs} that are expressive enough to represent any edge function. These GPs facilitate direct and independent learning for the different Hodge components of edge functions, enabling us to capture their relevance during hyperparameter optimization. To highlight their practical potential, we apply them for flow data inference in currency exchange, ocean flows and water supply networks, comparing them to alternative models.

ICML 2023 Topological Deep Learning Challenge : Design and Results

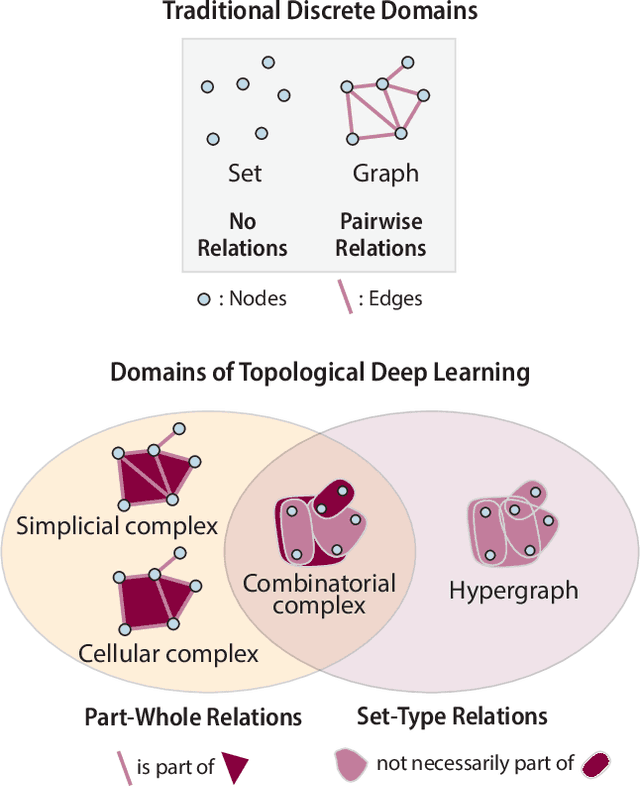
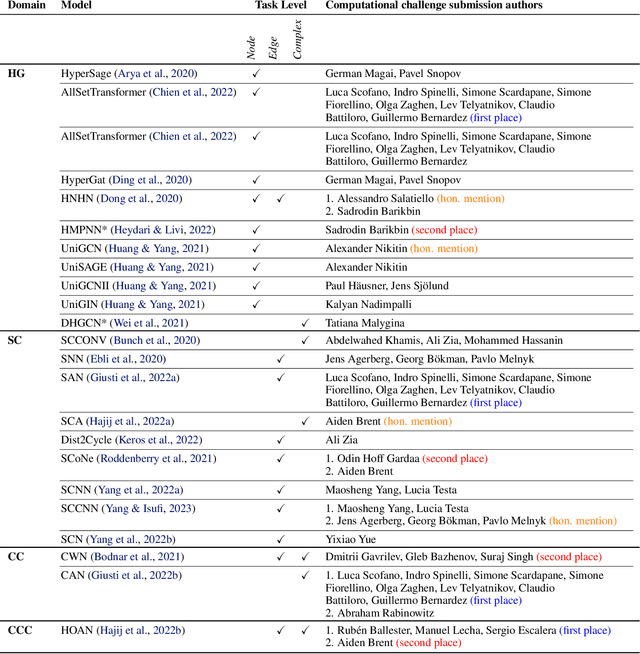
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Convolutional Learning on Simplicial Complexes

We propose a simplicial complex convolutional neural network (SCCNN) to learn data representations on simplicial complexes. It performs convolutions based on the multi-hop simplicial adjacencies via common faces and cofaces independently and captures the inter-simplicial couplings, generalizing state-of-the-art. Upon studying symmetries of the simplicial domain and the data space, it is shown to be permutation and orientation equivariant, thus, incorporating such inductive biases. Based on the Hodge theory, we perform a spectral analysis to understand how SCCNNs regulate data in different frequencies, showing that the convolutions via faces and cofaces operate in two orthogonal data spaces. Lastly, we study the stability of SCCNNs to domain deformations and examine the effects of various factors. Empirical results show the benefits of higher-order convolutions and inter-simplicial couplings in simplex prediction and trajectory prediction.

Convolutional Filtering in Simplicial Complexes

This paper proposes convolutional filtering for data whose structure can be modeled by a simplicial complex (SC). SCs are mathematical tools that not only capture pairwise relationships as graphs but account also for higher-order network structures. These filters are built by following the shift-and-sum principle of the convolution operation and rely on the Hodge-Laplacians to shift the signal within the simplex. But since in SCs we have also inter-simplex coupling, we use the incidence matrices to transfer the signal in adjacent simplices and build a filter bank to jointly filter signals from different levels. We prove some interesting properties for the proposed filter bank, including permutation and orientation equivariance, a computational complexity that is linear in the SC dimension, and a spectral interpretation using the simplicial Fourier transform. We illustrate the proposed approach with numerical experiments.

Simplicial Convolutional Filters

We study linear filters for processing signals supported on abstract topological spaces modeled as simplicial complexes, which may be interpreted as generalizations of graphs that account for nodes, edges, triangular faces etc. To process such signals, we develop simplicial convolutional filters defined as matrix polynomials of the lower and upper Hodge Laplacians. First, we study the properties of these filters and show that they are linear and shift-invariant, as well as permutation and orientation equivariant. These filters can also be implemented in a distributed fashion with a low computational complexity, as they involve only (multiple rounds of) simplicial shifting between upper and lower adjacent simplices. Second, focusing on edge-flows, we study the frequency responses of these filters and examine how we can use the Hodge-decomposition to delineate gradient, curl and harmonic frequencies. We discuss how these frequencies correspond to the lower- and the upper-adjacent couplings and the kernel of the Hodge Laplacian, respectively, and can be tuned independently by our filter designs. Third, we study different procedures for designing simplicial convolutional filters and discuss their relative advantages. Finally, we corroborate our simplicial filters in several applications: to extract different frequency components of a simplicial signal, to denoise edge flows, and to analyze financial markets and traffic networks.

Simplicial Convolutional Neural Networks

Graphs can model networked data by representing them as nodes and their pairwise relationships as edges. Recently, signal processing and neural networks have been extended to process and learn from data on graphs, with achievements in tasks like graph signal reconstruction, graph or node classifications, and link prediction. However, these methods are only suitable for data defined on the nodes of a graph. In this paper, we propose a simplicial convolutional neural network (SCNN) architecture to learn from data defined on simplices, e.g., nodes, edges, triangles, etc. We study the SCNN permutation and orientation equivariance, complexity, and spectral analysis. Finally, we test the SCNN performance for imputing citations on a coauthorship complex.

Finite Impulse Response Filters for Simplicial Complexes

In this paper, we study linear filters to process signals defined on simplicial complexes, i.e., signals defined on nodes, edges, triangles, etc. of a simplicial complex, thereby generalizing filtering operations for graph signals. We propose a finite impulse response filter based on the Hodge Laplacian, and demonstrate how this filter can be designed to amplify or attenuate certain spectral components of simplicial signals. Specifically, we discuss how, unlike in the case of node signals, the Fourier transform in the context of edge signals can be understood in terms of two orthogonal subspaces corresponding to the gradient-flow signals and curl-flow signals arising from the Hodge decomposition. By assigning different filter coefficients to the associated terms of the Hodge Laplacian, we develop a subspace-varying filter which enables more nuanced control over these signal types. Numerical experiments are conducted to show the potential of simplicial filters for sub-component extraction, denoising and model approximation.