Trees, Forests, Chickens, and Eggs: When and Why to Prune Trees in a Random Forest

Due to their long-standing reputation as excellent off-the-shelf predictors, random forests continue remain a go-to model of choice for applied statisticians and data scientists. Despite their widespread use, however, until recently, little was known about their inner-workings and about which aspects of the procedure were driving their success. Very recently, two competing hypotheses have emerged -- one based on interpolation and the other based on regularization. This work argues in favor of the latter by utilizing the regularization framework to reexamine the decades-old question of whether individual trees in an ensemble ought to be pruned. Despite the fact that default constructions of random forests use near full depth trees in most popular software packages, here we provide strong evidence that tree depth should be seen as a natural form of regularization across the entire procedure. In particular, our work suggests that random forests with shallow trees are advantageous when the signal-to-noise ratio in the data is low. In building up this argument, we also critique the newly popular notion of "double descent" in random forests by drawing parallels to U-statistics and arguing that the noticeable jumps in random forest accuracy are the result of simple averaging rather than interpolation.

Bridging Breiman's Brook: From Algorithmic Modeling to Statistical Learning

In 2001, Leo Breiman wrote of a divide between "data modeling" and "algorithmic modeling" cultures. Twenty years later this division feels far more ephemeral, both in terms of assigning individuals to camps, and in terms of intellectual boundaries. We argue that this is largely due to the "data modelers" incorporating algorithmic methods into their toolbox, particularly driven by recent developments in the statistical understanding of Breiman's own Random Forest methods. While this can be simplistically described as "Breiman won", these same developments also expose the limitations of the prediction-first philosophy that he espoused, making careful statistical analysis all the more important. This paper outlines these exciting recent developments in the random forest literature which, in our view, occurred as a result of a necessary blending of the two ways of thinking Breiman originally described. We also ask what areas statistics and statisticians might currently overlook.

Posterior Calibrated Training on Sentence Classification Tasks

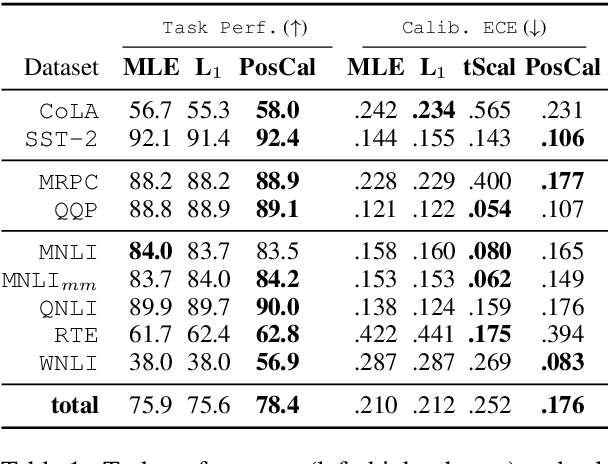
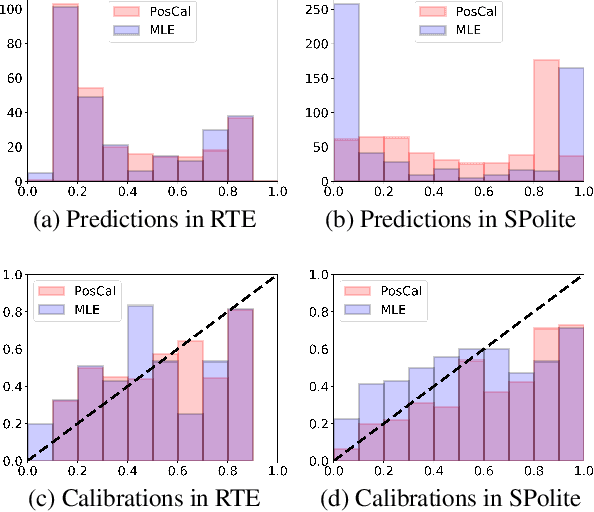
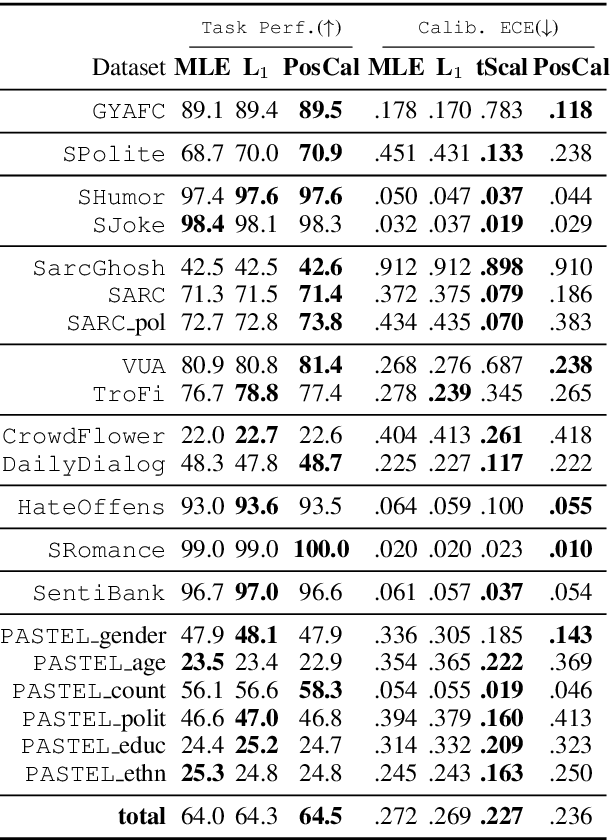
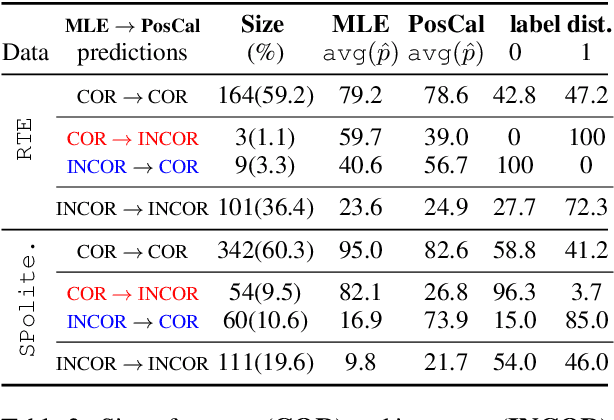
Most classification models work by first predicting a posterior probability distribution over all classes and then selecting that class with the largest estimated probability. In many settings however, the quality of posterior probability itself (e.g., 65% chance having diabetes), gives more reliable information than the final predicted class alone. When these methods are shown to be poorly calibrated, most fixes to date have relied on posterior calibration, which rescales the predicted probabilities but often has little impact on final classifications. Here we propose an end-to-end training procedure called posterior calibrated (PosCal) training that directly optimizes the objective while minimizing the difference between the predicted and empirical posterior probabilities.We show that PosCal not only helps reduce the calibration error but also improve task performance by penalizing drops in performance of both objectives. Our PosCal achieves about 2.5% of task performance gain and 16.1% of calibration error reduction on GLUE (Wang et al., 2018) compared to the baseline. We achieved the comparable task performance with 13.2% calibration error reduction on xSLUE (Kang and Hovy, 2019), but not outperforming the two-stage calibration baseline. PosCal training can be easily extendable to any types of classification tasks as a form of regularization term. Also, PosCal has the advantage that it incrementally tracks needed statistics for the calibration objective during the training process, making efficient use of large training sets.

Getting Better from Worse: Augmented Bagging and a Cautionary Tale of Variable Importance

As the size, complexity, and availability of data continues to grow, scientists are increasingly relying upon black-box learning algorithms that can often provide accurate predictions with minimal a priori model specifications. Tools like random forest have an established track record of off-the-shelf success and even offer various strategies for analyzing the underlying relationships between features and the response. Motivated by recent insights into random forest behavior, here we introduce the idea of augmented bagging (AugBagg), a procedure that operates in an identical fashion to the classical bagging and random forest counterparts but which operates on a larger space containing additional, randomly generated features. Somewhat surprisingly, we demonstrate that the simple act of adding additional random features into the model can have a dramatic beneficial effect on performance, sometimes outperforming even an optimally tuned traditional random forest. This finding that the inclusion of an additional set of features generated independently of the response can considerably improve predictive performance has crucial implications for the manner in which we consider and measure variable importance. Numerous demonstrations on both real and synthetic data are provided.

Asymptotic Normality and Variance Estimation For Supervised Ensembles

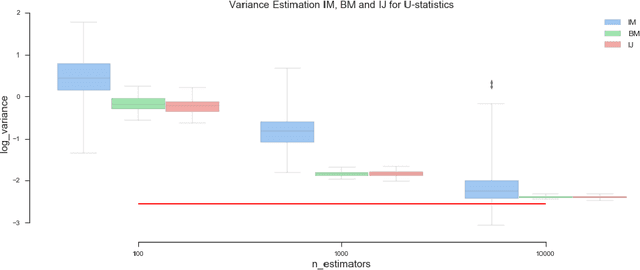
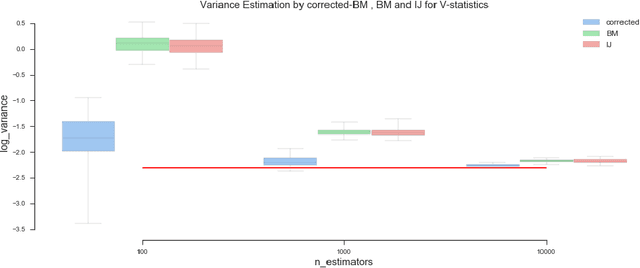
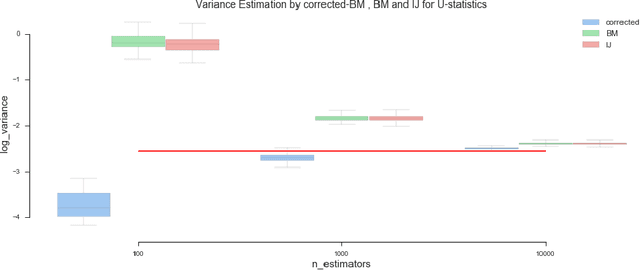
Ensemble methods based on bootstrapping have improved the predictive accuracy of base learners, but fail to provide a framework in which formal statistical inference can be conducted. Recent theoretical developments suggest taking subsamples without replacement and analyze the resulting estimator in the context of a U-statistic, thus demonstrating asymptotic normality properties. However, we observe that current methods for variance estimation exhibit severe bias when the number of base learners is not large enough, compromising the validity of the resulting confidence intervals or hypothesis tests. This paper shows that similar asymptotics can be achieved by means of V-statistics, corresponding to taking subsamples with replacement. Further, we develop a bias correction algorithm for estimating variance in the limiting distribution, which yields satisfactory results with moderate size of base learners.

Randomization as Regularization: A Degrees of Freedom Explanation for Random Forest Success

Random forests remain among the most popular off-the-shelf supervised machine learning tools with a well-established track record of predictive accuracy in both regression and classification settings. Despite their empirical success as well as a bevy of recent work investigating their statistical properties, a full and satisfying explanation for their success has yet to be put forth. Here we aim to take a step forward in this direction by demonstrating that the additional randomness injected into individual trees serves as a form of implicit regularization, making random forests an ideal model in low signal-to-noise ratio (SNR) settings. Specifically, from a model-complexity perspective, we show that the mtry parameter in random forests serves much the same purpose as the shrinkage penalty in explicitly regularized regression procedures like lasso and ridge regression. To highlight this point, we design a randomized linear-model-based forward selection procedure intended as an analogue to tree-based random forests and demonstrate its surprisingly strong empirical performance. Numerous demonstrations on both real and synthetic data are provided.

Earlier Isn't Always Better: Sub-aspect Analysis on Corpus and System Biases in Summarization

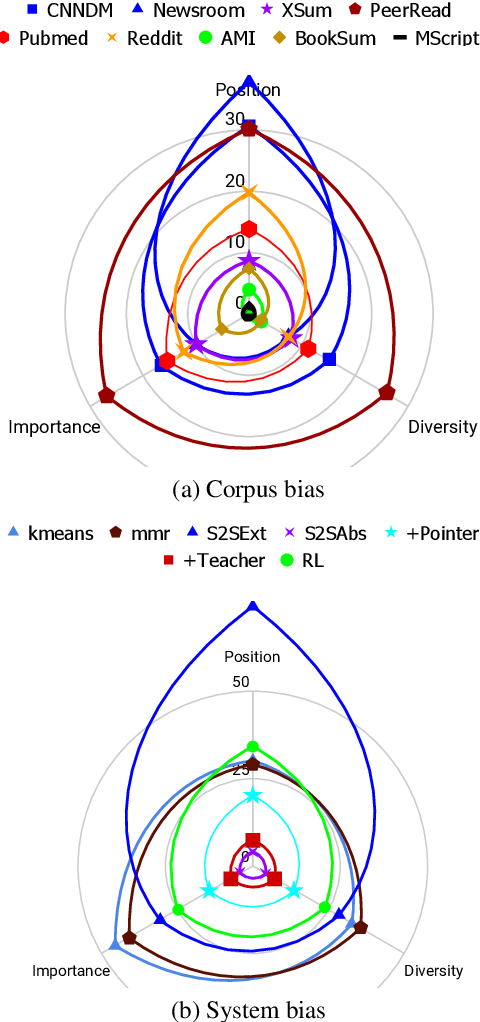
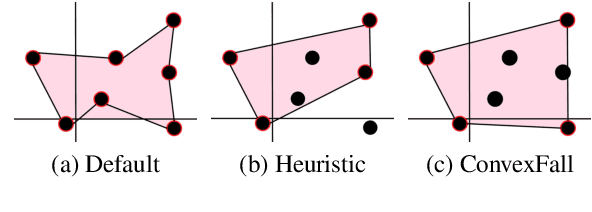
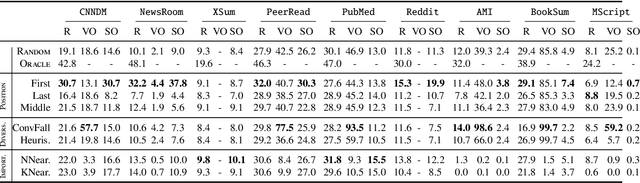
Despite the recent developments on neural summarization systems, the underlying logic behind the improvements from the systems and its corpus-dependency remains largely unexplored. Position of sentences in the original text, for example, is a well known bias for news summarization. Following in the spirit of the claim that summarization is a combination of sub-functions, we define three sub-aspects of summarization: position, importance, and diversity and conduct an extensive analysis of the biases of each sub-aspect with respect to the domain of nine different summarization corpora (e.g., news, academic papers, meeting minutes, movie script, books, posts). We find that while position exhibits substantial bias in news articles, this is not the case, for example, with academic papers and meeting minutes. Furthermore, our empirical study shows that different types of summarization systems (e.g., neural-based) are composed of different degrees of the sub-aspects. Our study provides useful lessons regarding consideration of underlying sub-aspects when collecting a new summarization dataset or developing a new system.

Locally Optimized Random Forests

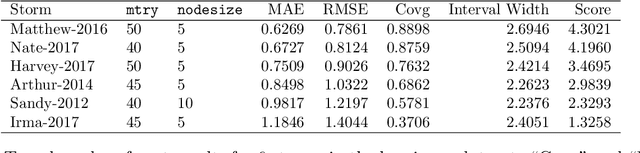
Standard supervised learning procedures are validated against a test set that is assumed to have come from the same distribution as the training data. However, in many problems, the test data may have come from a different distribution. We consider the case of having many labeled observations from one distribution, $P_1$, and making predictions at unlabeled points that come from $P_2$. We combine the high predictive accuracy of random forests (Breiman, 2001) with an importance sampling scheme, where the splits and predictions of the base-trees are done in a weighted manner, which we call Locally Optimized Random Forests. These weights correspond to a non-parametric estimate of the likelihood ratio between the training and test distributions. To estimate these ratios with an unlabeled test set, we make the covariate shift assumption, where the differences in distribution are only a function of the training distributions (Shimodaira, 2000.) This methodology is motivated by the problem of forecasting power outages during hurricanes. The extreme nature of the most devastating hurricanes means that typical validation set ups will overly favor less extreme storms. Our method provides a data-driven means of adapting a machine learning method to deal with extreme events.

Asymptotic Distributions and Rates of Convergence for Random Forests and other Resampled Ensemble Learners

Random forests remain among the most popular off-the-shelf supervised learning algorithms. Despite their well-documented empirical success, however, until recently, few theoretical results were available to describe their performance and behavior. In this work we push beyond recent work on consistency and asymptotic normality by establishing rates of convergence for random forests and other supervised learning ensembles. We develop the notion of generalized U-statistics and show that within this framework, random forest predictions remain asymptotically normal for larger subsample sizes than previously established. We also provide Berry-Esseen bounds in order to quantify the rate at which this convergence occurs, making explicit the roles of the subsample size and the number of trees in determining the distribution of random forest predictions.

Please Stop Permuting Features: An Explanation and Alternatives

This paper advocates against permute-and-predict (PaP) methods for interpreting black box functions. Methods such as the variable importance measures proposed for random forests, partial dependence plots, and individual conditional expectation plots remain popular because of their ability to provide model-agnostic measures that depend only on the pre-trained model output. However, numerous studies have found that these tools can produce diagnostics that are highly misleading, particularly when there is strong dependence among features. Rather than simply add to this growing literature by further demonstrating such issues, here we seek to provide an explanation for the observed behavior. In particular, we argue that breaking dependencies between features in hold-out data places undue emphasis on sparse regions of the feature space by forcing the original model to extrapolate to regions where there is little to no data. We explore these effects through various settings where a ground-truth is understood and find support for previous claims in the literature that PaP metrics tend to over-emphasize correlated features both in variable importance and partial dependence plots, even though applying permutation methods to the ground-truth models do not. As an alternative, we recommend more direct approaches that have proven successful in other settings: explicitly removing features, conditional permutations, or model distillation methods.