Asymptotic Normality and Variance Estimation For Supervised Ensembles

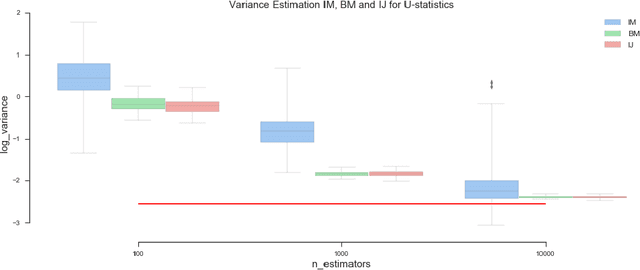
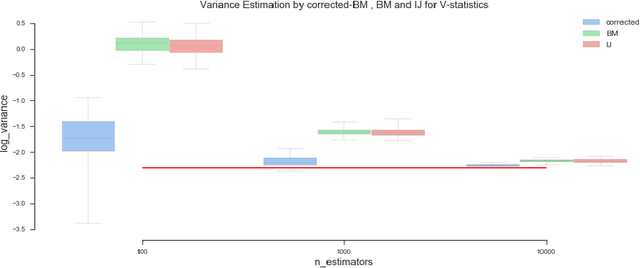
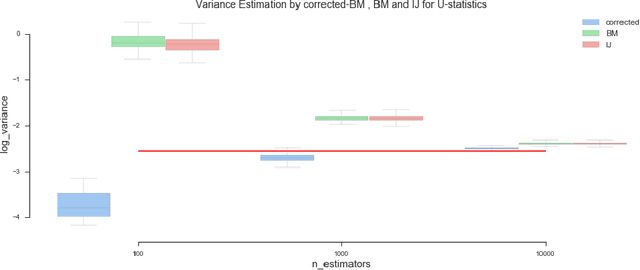
Ensemble methods based on bootstrapping have improved the predictive accuracy of base learners, but fail to provide a framework in which formal statistical inference can be conducted. Recent theoretical developments suggest taking subsamples without replacement and analyze the resulting estimator in the context of a U-statistic, thus demonstrating asymptotic normality properties. However, we observe that current methods for variance estimation exhibit severe bias when the number of base learners is not large enough, compromising the validity of the resulting confidence intervals or hypothesis tests. This paper shows that similar asymptotics can be achieved by means of V-statistics, corresponding to taking subsamples with replacement. Further, we develop a bias correction algorithm for estimating variance in the limiting distribution, which yields satisfactory results with moderate size of base learners.