Trend Filtered Mixture of Experts for Automated Gating of High-Frequency Flow Cytometry Data

Ocean microbes are critical to both ocean ecosystems and the global climate. Flow cytometry, which measures cell optical properties in fluid samples, is routinely used in oceanographic research. Despite decades of accumulated data, identifying key microbial populations (a process known as ``gating'') remains a significant analytical challenge. To address this, we focus on gating multidimensional, high-frequency flow cytometry data collected {\it continuously} on board oceanographic research vessels, capturing time- and space-wise variations in the dynamic ocean. Our paper proposes a novel mixture-of-experts model in which both the gating function and the experts are given by trend filtering. The model leverages two key assumptions: (1) Each snapshot of flow cytometry data is a mixture of multivariate Gaussians and (2) the parameters of these Gaussians vary smoothly over time. Our method uses regularization and a constraint to ensure smoothness and that cluster means match biologically distinct microbe types. We demonstrate, using flow cytometry data from the North Pacific Ocean, that our proposed model accurately matches human-annotated gating and corrects significant errors.

Locally Optimized Random Forests

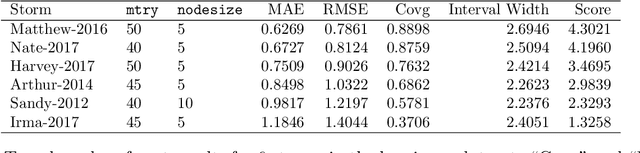
Standard supervised learning procedures are validated against a test set that is assumed to have come from the same distribution as the training data. However, in many problems, the test data may have come from a different distribution. We consider the case of having many labeled observations from one distribution, $P_1$, and making predictions at unlabeled points that come from $P_2$. We combine the high predictive accuracy of random forests (Breiman, 2001) with an importance sampling scheme, where the splits and predictions of the base-trees are done in a weighted manner, which we call Locally Optimized Random Forests. These weights correspond to a non-parametric estimate of the likelihood ratio between the training and test distributions. To estimate these ratios with an unlabeled test set, we make the covariate shift assumption, where the differences in distribution are only a function of the training distributions (Shimodaira, 2000.) This methodology is motivated by the problem of forecasting power outages during hurricanes. The extreme nature of the most devastating hurricanes means that typical validation set ups will overly favor less extreme storms. Our method provides a data-driven means of adapting a machine learning method to deal with extreme events.

Asymptotic Distributions and Rates of Convergence for Random Forests and other Resampled Ensemble Learners

Random forests remain among the most popular off-the-shelf supervised learning algorithms. Despite their well-documented empirical success, however, until recently, few theoretical results were available to describe their performance and behavior. In this work we push beyond recent work on consistency and asymptotic normality by establishing rates of convergence for random forests and other supervised learning ensembles. We develop the notion of generalized U-statistics and show that within this framework, random forest predictions remain asymptotically normal for larger subsample sizes than previously established. We also provide Berry-Esseen bounds in order to quantify the rate at which this convergence occurs, making explicit the roles of the subsample size and the number of trees in determining the distribution of random forest predictions.

Scalable and Efficient Hypothesis Testing with Random Forests

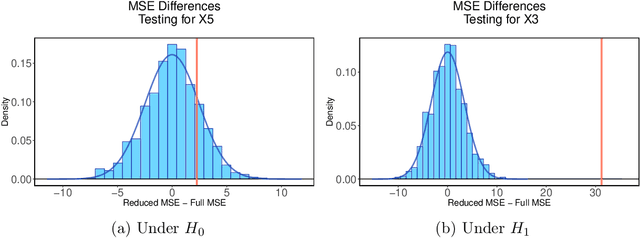
Throughout the last decade, random forests have established themselves as among the most accurate and popular supervised learning methods. While their black-box nature has made their mathematical analysis difficult, recent work has established important statistical properties like consistency and asymptotic normality by considering subsampling in lieu of bootstrapping. Though such results open the door to traditional inference procedures, all formal methods suggested thus far place severe restrictions on the testing framework and their computational overhead precludes their practical scientific use. Here we propose a permutation-style testing approach to formally assess feature significance. We establish asymptotic validity of the test via exchangeability arguments and show that the test maintains high power with orders of magnitude fewer computations. As importantly, the procedure scales easily to big data settings where large training and testing sets may be employed without the need to construct additional models. Simulations and applications to ecological data where random forests have recently shown promise are provided.