An Adaptive Open-Source Dataset Generation Framework for Machine Learning Tasks in Logic Synthesis

This paper introduces an adaptive logic synthesis dataset generation framework designed to enhance machine learning applications within the logic synthesis process. Unlike previous dataset generation flows that were tailored for specific tasks or lacked integrated machine learning capabilities, the proposed framework supports a comprehensive range of machine learning tasks by encapsulating the three fundamental steps of logic synthesis: Boolean representation, logic optimization, and technology mapping. It preserves the original information in the intermediate files that can be stored in both Verilog and Graphmal format. Verilog files enable semi-customizability, allowing researchers to add steps and incrementally refine the generated dataset. The framework also includes an adaptive circuit engine to facilitate the loading of GraphML files for final dataset packaging and sub-dataset extraction. The generated OpenLS-D dataset comprises 46 combinational designs from established benchmarks, totaling over 966,000 Boolean circuits, with each design containing 21,000 circuits generated from 1000 synthesis recipes, including 7000 Boolean networks, 7000 ASIC netlists, and 7000 FPGA netlists. Furthermore, OpenLS-D supports integrating newly desired data features, making it more versatile for new challenges. The utility of OpenLS-D is demonstrated through four distinct downstream tasks: circuit classification, circuit ranking, quality of results (QoR) prediction, and probability prediction. Each task highlights different internal steps of logic synthesis, with the datasets extracted and relabeled from the OpenLS-D dataset using the circuit engine. The experimental results confirm the dataset's diversity and extensive applicability. The source code and datasets are available at https://github.com/Logic-Factory/ACE/blob/master/OpenLS-D/readme.md.

Adaptive Reconvergence-driven AIG Rewriting via Strategy Learning

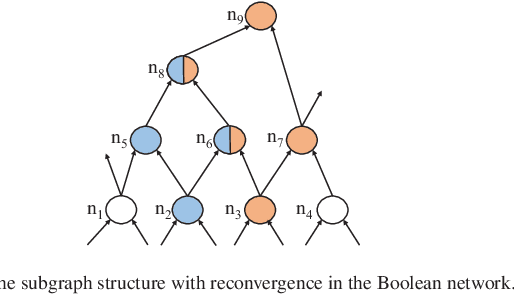
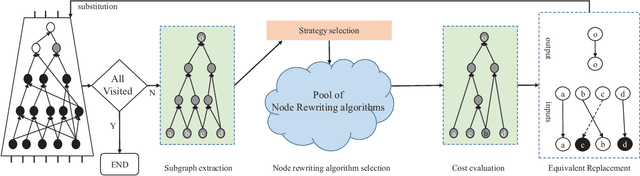
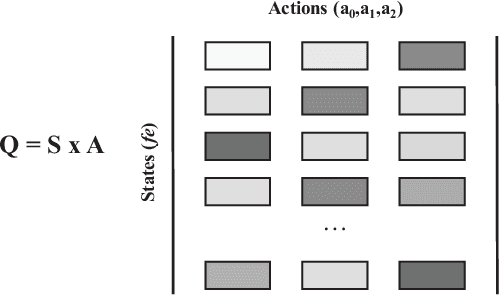
Rewriting is a common procedure in logic synthesis aimed at improving the performance, power, and area (PPA) of circuits. The traditional reconvergence-driven And-Inverter Graph (AIG) rewriting method focuses solely on optimizing the reconvergence cone through Boolean algebra minimization. However, there exist opportunities to incorporate other node-rewriting algorithms that are better suited for specific cones. In this paper, we propose an adaptive reconvergence-driven AIG rewriting algorithm that combines two key techniques: multi-strategy-based AIG rewriting and strategy learning-based algorithm selection. The multi-strategy-based rewriting method expands upon the traditional approach by incorporating support for multi-node-rewriting algorithms, thus expanding the optimization space. Additionally, the strategy learning-based algorithm selection method determines the most suitable node-rewriting algorithm for a given cone. Experimental results demonstrate that our proposed method yields a significant average improvement of 5.567\% in size and 5.327\% in depth.

Fast Exact NPN Classification with Influence-aided Canonical Form

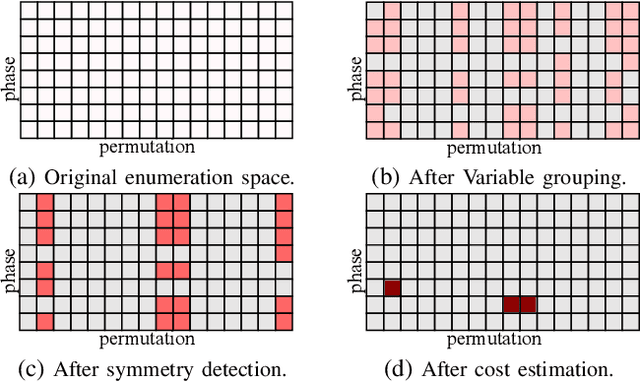
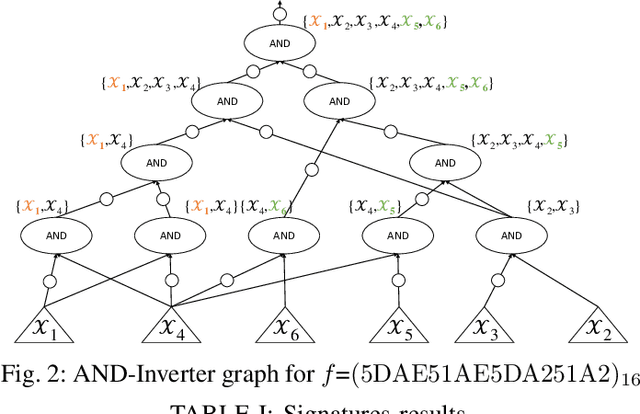
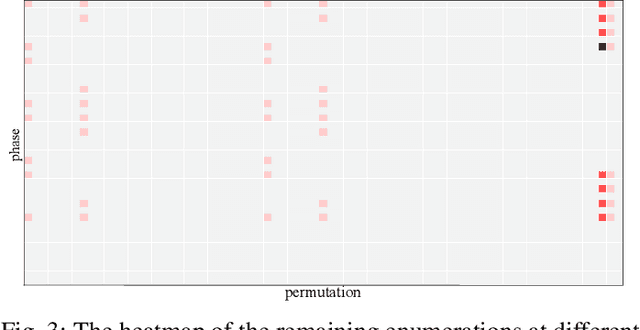
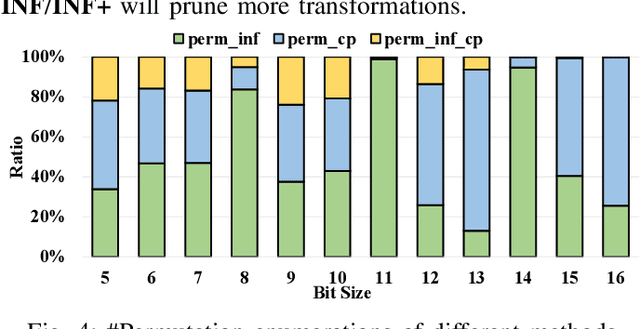
NPN classification has many applications in the synthesis and verification of digital circuits. The canonical-form-based method is the most common approach, designing a canonical form as representative for the NPN equivalence class first and then computing the transformation function according to the canonical form. Most works use variable symmetries and several signatures, mainly based on the cofactor, to simplify the canonical form construction and computation. This paper describes a novel canonical form and its computation algorithm by introducing Boolean influence to NPN classification, which is a basic concept in analysis of Boolean functions. We show that influence is input-negation-independent, input-permutation-dependent, and has other structural information than previous signatures for NPN classification. Therefore, it is a significant ingredient in speeding up NPN classification. Experimental results prove that influence plays an important role in reducing the transformation enumeration in computing the canonical form. Compared with the state-of-the-art algorithm implemented in ABC, our influence-aided canonical form for exact NPN classification gains up to 5.5x speedup.

Enhanced Fast Boolean Matching based on Sensitivity Signatures Pruning

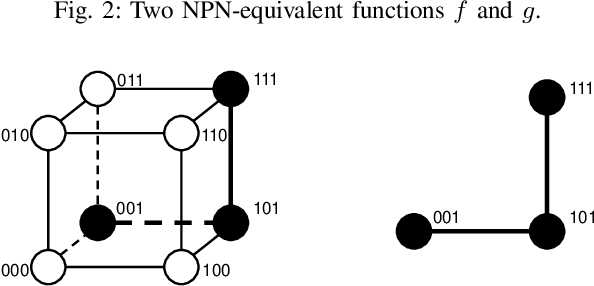
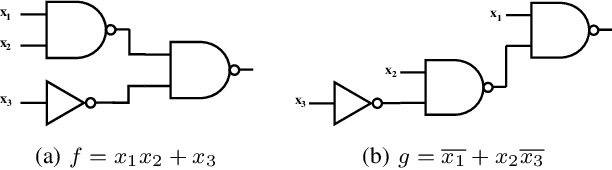
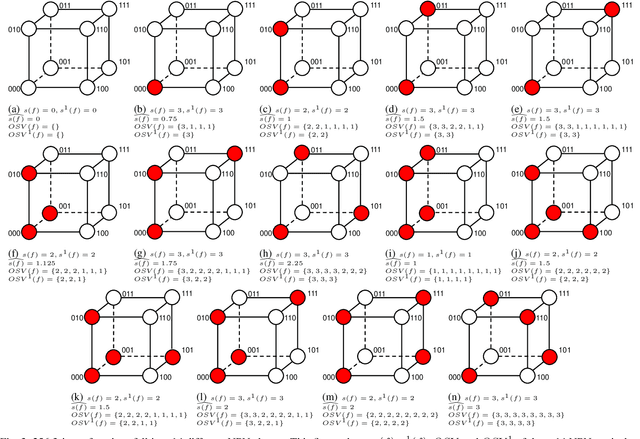
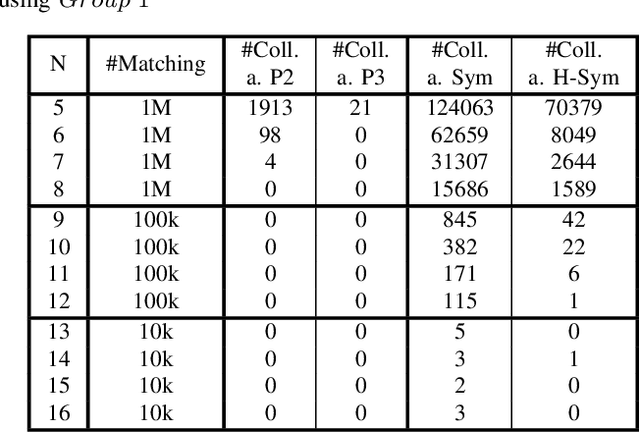
Boolean matching is significant to digital integrated circuits design. An exhaustive method for Boolean matching is computationally expensive even for functions with only a few variables, because the time complexity of such an algorithm for an n-variable Boolean function is $O(2^{n+1}n!)$. Sensitivity is an important characteristic and a measure of the complexity of Boolean functions. It has been used in analysis of the complexity of algorithms in different fields. This measure could be regarded as a signature of Boolean functions and has great potential to help reduce the search space of Boolean matching. In this paper, we introduce Boolean sensitivity into Boolean matching and design several sensitivity-related signatures to enhance fast Boolean matching. First, we propose some new signatures that relate sensitivity to Boolean equivalence. Then, we prove that these signatures are prerequisites for Boolean matching, which we can use to reduce the search space of the matching problem. Besides, we develop a fast sensitivity calculation method to compute and compare these signatures of two Boolean functions. Compared with the traditional cofactor and symmetric detection methods, sensitivity is a series of signatures of another dimension. We also show that sensitivity can be easily integrated into traditional methods and distinguish the mismatched Boolean functions faster. To the best of our knowledge, this is the first work that introduces sensitivity to Boolean matching. The experimental results show that sensitivity-related signatures we proposed in this paper can reduce the search space to a very large extent, and perform up to 3x speedup over the state-of-the-art Boolean matching methods.