Xiangfu Zou
Enhanced Fast Boolean Matching based on Sensitivity Signatures Pruning
Nov 11, 2021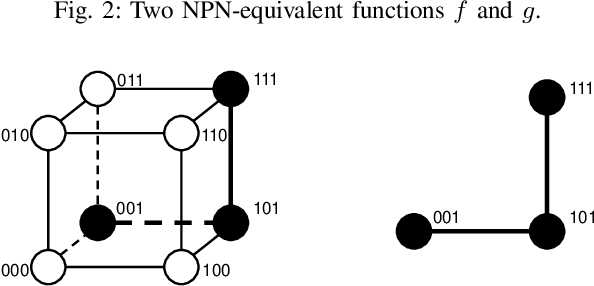
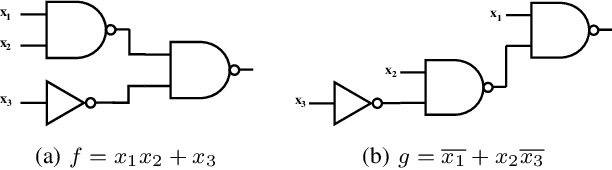
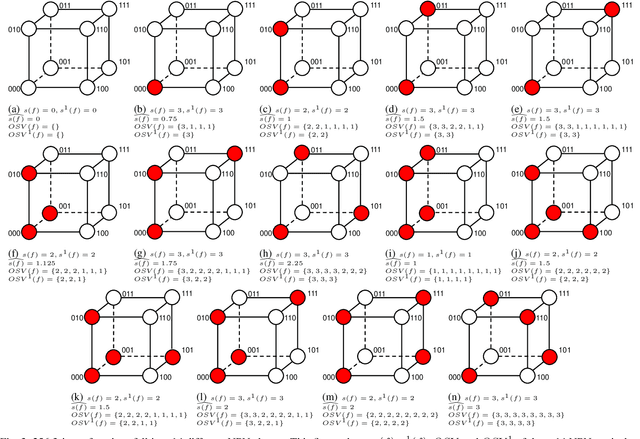
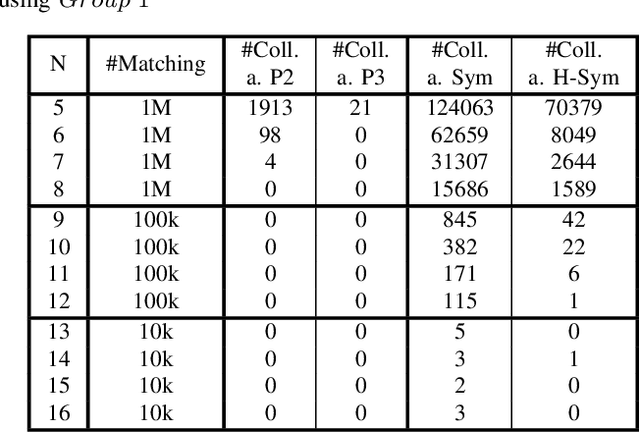
Abstract:Boolean matching is significant to digital integrated circuits design. An exhaustive method for Boolean matching is computationally expensive even for functions with only a few variables, because the time complexity of such an algorithm for an n-variable Boolean function is $O(2^{n+1}n!)$. Sensitivity is an important characteristic and a measure of the complexity of Boolean functions. It has been used in analysis of the complexity of algorithms in different fields. This measure could be regarded as a signature of Boolean functions and has great potential to help reduce the search space of Boolean matching. In this paper, we introduce Boolean sensitivity into Boolean matching and design several sensitivity-related signatures to enhance fast Boolean matching. First, we propose some new signatures that relate sensitivity to Boolean equivalence. Then, we prove that these signatures are prerequisites for Boolean matching, which we can use to reduce the search space of the matching problem. Besides, we develop a fast sensitivity calculation method to compute and compare these signatures of two Boolean functions. Compared with the traditional cofactor and symmetric detection methods, sensitivity is a series of signatures of another dimension. We also show that sensitivity can be easily integrated into traditional methods and distinguish the mismatched Boolean functions faster. To the best of our knowledge, this is the first work that introduces sensitivity to Boolean matching. The experimental results show that sensitivity-related signatures we proposed in this paper can reduce the search space to a very large extent, and perform up to 3x speedup over the state-of-the-art Boolean matching methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge