Fast Exact NPN Classification with Influence-aided Canonical Form

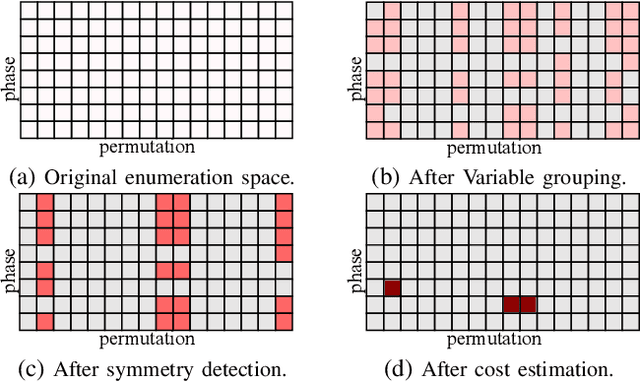
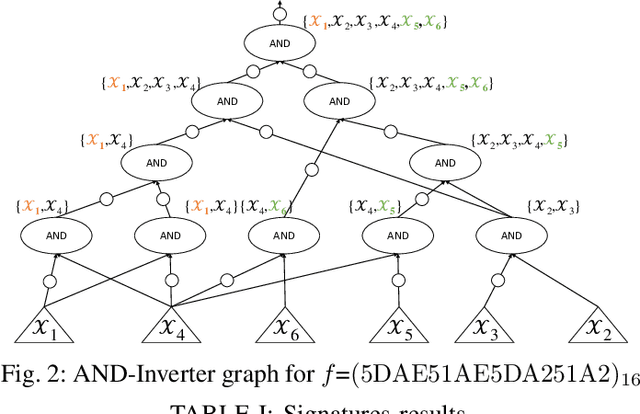
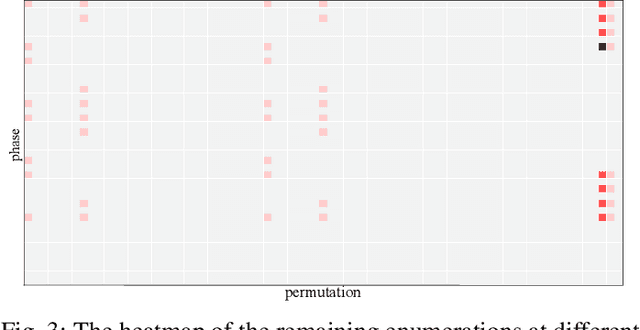
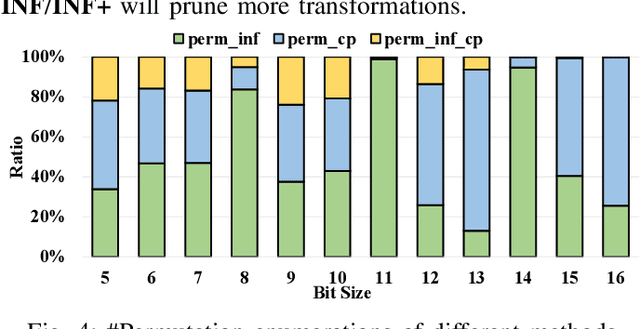
NPN classification has many applications in the synthesis and verification of digital circuits. The canonical-form-based method is the most common approach, designing a canonical form as representative for the NPN equivalence class first and then computing the transformation function according to the canonical form. Most works use variable symmetries and several signatures, mainly based on the cofactor, to simplify the canonical form construction and computation. This paper describes a novel canonical form and its computation algorithm by introducing Boolean influence to NPN classification, which is a basic concept in analysis of Boolean functions. We show that influence is input-negation-independent, input-permutation-dependent, and has other structural information than previous signatures for NPN classification. Therefore, it is a significant ingredient in speeding up NPN classification. Experimental results prove that influence plays an important role in reducing the transformation enumeration in computing the canonical form. Compared with the state-of-the-art algorithm implemented in ABC, our influence-aided canonical form for exact NPN classification gains up to 5.5x speedup.

Enhanced Fast Boolean Matching based on Sensitivity Signatures Pruning

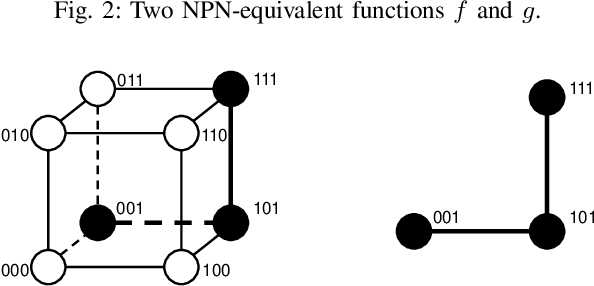
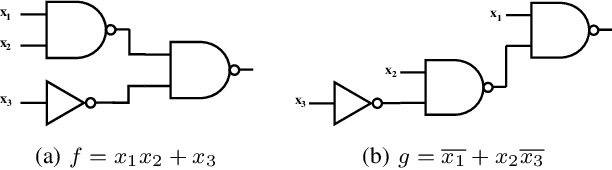
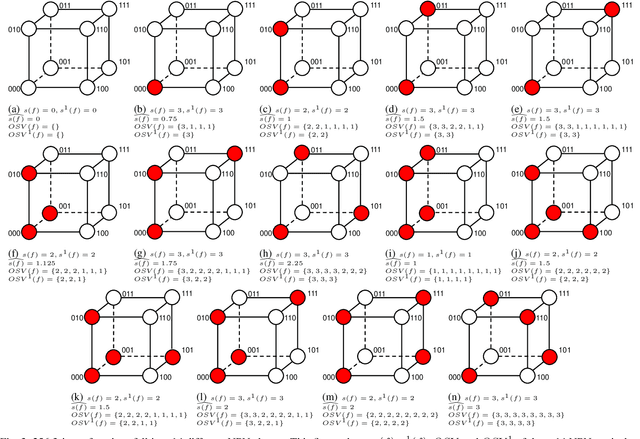
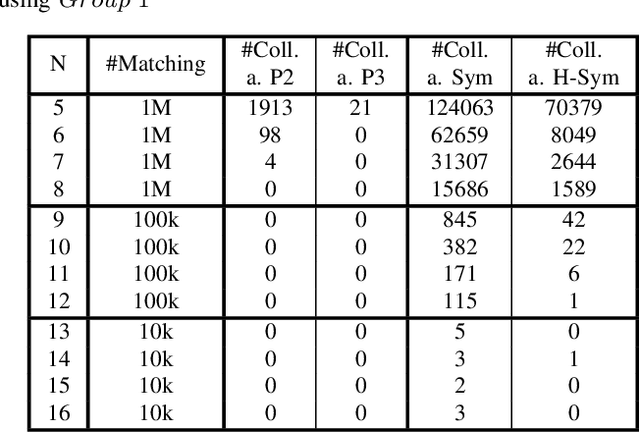
Boolean matching is significant to digital integrated circuits design. An exhaustive method for Boolean matching is computationally expensive even for functions with only a few variables, because the time complexity of such an algorithm for an n-variable Boolean function is $O(2^{n+1}n!)$. Sensitivity is an important characteristic and a measure of the complexity of Boolean functions. It has been used in analysis of the complexity of algorithms in different fields. This measure could be regarded as a signature of Boolean functions and has great potential to help reduce the search space of Boolean matching. In this paper, we introduce Boolean sensitivity into Boolean matching and design several sensitivity-related signatures to enhance fast Boolean matching. First, we propose some new signatures that relate sensitivity to Boolean equivalence. Then, we prove that these signatures are prerequisites for Boolean matching, which we can use to reduce the search space of the matching problem. Besides, we develop a fast sensitivity calculation method to compute and compare these signatures of two Boolean functions. Compared with the traditional cofactor and symmetric detection methods, sensitivity is a series of signatures of another dimension. We also show that sensitivity can be easily integrated into traditional methods and distinguish the mismatched Boolean functions faster. To the best of our knowledge, this is the first work that introduces sensitivity to Boolean matching. The experimental results show that sensitivity-related signatures we proposed in this paper can reduce the search space to a very large extent, and perform up to 3x speedup over the state-of-the-art Boolean matching methods.

Variational quantum compiling with double Q-learning

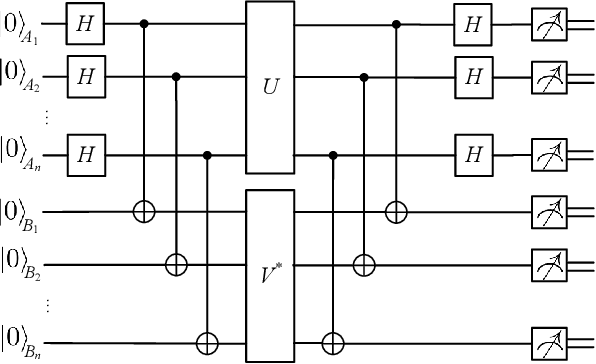
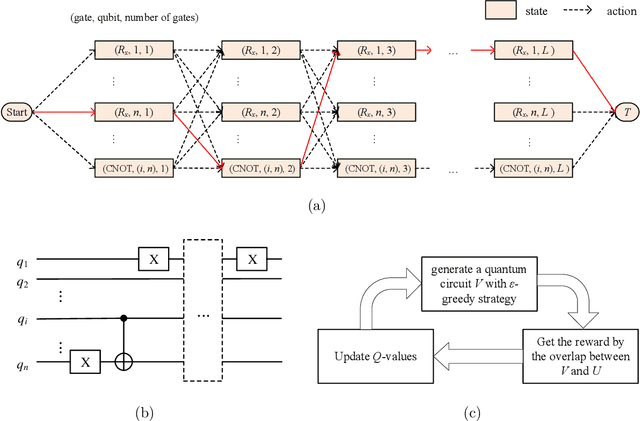
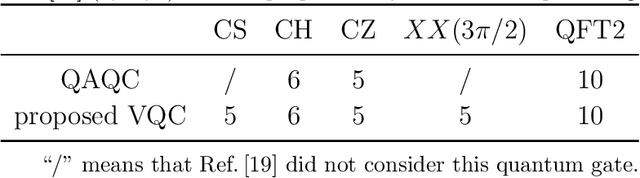
Quantum compiling aims to construct a quantum circuit V by quantum gates drawn from a native gate alphabet, which is functionally equivalent to the target unitary U. It is a crucial stage for the running of quantum algorithms on noisy intermediate-scale quantum (NISQ) devices. However, the space for structure exploration of quantum circuit is enormous, resulting in the requirement of human expertise, hundreds of experimentations or modifications from existing quantum circuits. In this paper, we propose a variational quantum compiling (VQC) algorithm based on reinforcement learning (RL), in order to automatically design the structure of quantum circuit for VQC with no human intervention. An agent is trained to sequentially select quantum gates from the native gate alphabet and the qubits they act on by double Q-learning with \epsilon-greedy exploration strategy and experience replay. At first, the agent randomly explores a number of quantum circuits with different structures, and then iteratively discovers structures with higher performance on the learning task. Simulation results show that the proposed method can make exact compilations with less quantum gates compared to previous VQC algorithms. It can reduce the errors of quantum algorithms due to decoherence process and gate noise in NISQ devices, and enable quantum algorithms especially for complex algorithms to be executed within coherence time.

RNA-2QCFA: Evolving Two-way Quantum Finite Automata with Classical States for RNA Secondary Structures

Recently, the use of mathematical methods and computer science applications have got significant response among biochemists and biologists to modeling the biological systems. The computational and mathematical methods have enormous potential for modeling the deoxyribonucleic acid (DNA) and ribonucleic acid (RNA) structures. The modeling of DNA and RNA secondary structures using automata theory had a significant impact in the fields of computer science. It is a natural goal to model the RNA secondary biomolecular structures using quantum computational models. Two-way quantum finite automata with classical states are more dominant than two-way probabilistic finite automata in language recognition. The main objective of this paper is on using two-way quantum finite automata with classical states to simulate, model and analyze the ribonucleic acid (RNA) sequences.

QPSO-CD: Quantum-behaved Particle Swarm Optimization Algorithm with Cauchy Distribution

Motivated by particle swarm optimization (PSO) and quantum computing theory, we have presented a quantum variant of PSO (QPSO) mutated with Cauchy operator and natural selection mechanism (QPSO-CD) from evolutionary computations. The performance of proposed hybrid quantum-behaved particle swarm optimization with Cauchy distribution (QPSO-CD) is investigated and compared with its counterparts based on a set of benchmark problems. Moreover, QPSO-CD is employed in well-studied constrained engineering problems to investigate its applicability. Further, the correctness and time complexity of QPSO-CD are analysed and compared with the classical PSO. It has been proven that QPSO-CD handles such real-life problems efficiently and can attain superior solutions in most of the problems. The experimental results showed that QPSO associated with Cauchy distribution and natural selection strategy outperforms other variants in the context of stability and convergence.