Lvzhou Li
Continual learning of quantum state classification with gradient episodic memory
Mar 26, 2022



Abstract:Continual learning is one of the many areas of machine learning research. For the goal of strong artificial intelligence that can mimic human-level intelligence, AI systems would have the ability to adapt to ever-changing scenarios and learn new knowledge continuously without forgetting previously acquired knowledge. A phenomenon called catastrophic forgetting emerges when a machine learning model is trained across multiple tasks. The model's performance on previously learned tasks may drop dramatically during the learning process of the newly seen task. Some continual learning strategies have been proposed to address the catastrophic forgetting problem. Recently, continual learning has also been studied in the context of quantum machine learning. By leveraging the elastic weight consolidation method, a single quantum classifier can perform multiple tasks after being trained consecutively on those tasks. In this work, we incorporate the gradient episodic memory method to train a variational quantum classifier. The gradient of the current task is projected to the closest gradient, avoiding the increase of the loss at previous tasks, but allowing the decrease. We use six quantum state classification tasks to benchmark this method. Numerical simulation results show that better performance is obtained compared to the elastic weight consolidation method. Furthermore, positive transfer of knowledge to previous tasks is observed, which means the classifier's performance on previous tasks is enhanced rather than compromised while learning a new task.
Variational quantum compiling with double Q-learning
Mar 22, 2021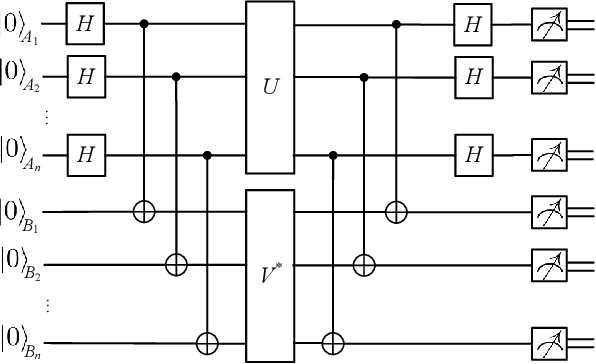

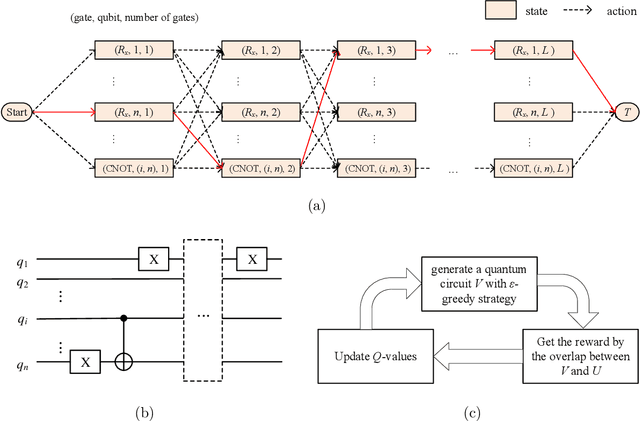
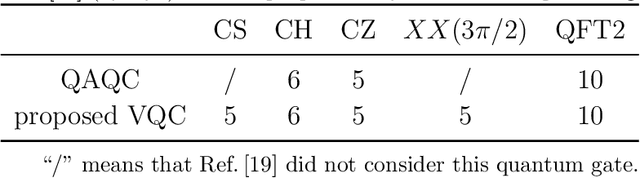
Abstract:Quantum compiling aims to construct a quantum circuit V by quantum gates drawn from a native gate alphabet, which is functionally equivalent to the target unitary U. It is a crucial stage for the running of quantum algorithms on noisy intermediate-scale quantum (NISQ) devices. However, the space for structure exploration of quantum circuit is enormous, resulting in the requirement of human expertise, hundreds of experimentations or modifications from existing quantum circuits. In this paper, we propose a variational quantum compiling (VQC) algorithm based on reinforcement learning (RL), in order to automatically design the structure of quantum circuit for VQC with no human intervention. An agent is trained to sequentially select quantum gates from the native gate alphabet and the qubits they act on by double Q-learning with \epsilon-greedy exploration strategy and experience replay. At first, the agent randomly explores a number of quantum circuits with different structures, and then iteratively discovers structures with higher performance on the learning task. Simulation results show that the proposed method can make exact compilations with less quantum gates compared to previous VQC algorithms. It can reduce the errors of quantum algorithms due to decoherence process and gate noise in NISQ devices, and enable quantum algorithms especially for complex algorithms to be executed within coherence time.
* 21 pages, 10 figures
Online Convex Optimization with Classical and Quantum Evaluation Oracles
Aug 01, 2020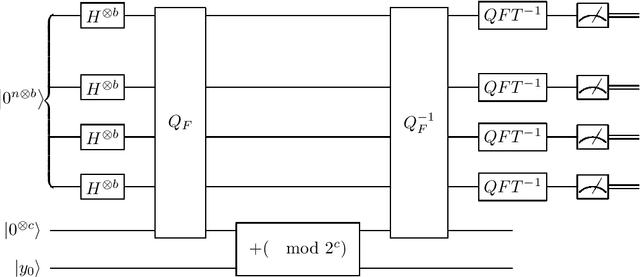
Abstract:As a fundamental tool in AI, convex optimization has been a significant research field for many years, and the same goes for its online version. Recently, general convex optimization problem has been accelerated with the help of quantum computing, and the technique of online convex optimization has been used for accelerating the online quantum state learning problem, thus we want to study whether online convex optimization (OCO) model can also be benefited from quantum computing. In this paper, we consider the OCO model, which can be described as a $T$ round iterative game between the player and the adversary. A key factor for measuring the performance of an OCO algorithm ${\cal A}$ is the regret denoted by $\text{regret}_{T}(\mathcal{A})$, and it is said to perform well if its regret is sublinear as a function of $T$. Another factor is the computational cost (e.g., query complexity) of the algorithm. We give a quantum algorithm for the online convex optimization model with only zeroth-order oracle available, which can achieve $O(\sqrt{T})$ and $O(\log{T})$ regret for general convex loss functions and $\alpha$-strong loss functions respectively, where only $O(1)$ queries are needed in each round. Our results show that the zeroth-order quantum oracle is as powerful as the classical first-order oracle, and show potential advantages of quantum computing over classical computing in the OCO model where only zeroth-order oracle available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge