AscendKernelGen: A Systematic Study of LLM-Based Kernel Generation for Neural Processing Units

To meet the ever-increasing demand for computational efficiency, Neural Processing Units (NPUs) have become critical in modern AI infrastructure. However, unlocking their full potential requires developing high-performance compute kernels using vendor-specific Domain-Specific Languages (DSLs), a task that demands deep hardware expertise and is labor-intensive. While Large Language Models (LLMs) have shown promise in general code generation, they struggle with the strict constraints and scarcity of training data in the NPU domain. Our preliminary study reveals that state-of-the-art general-purpose LLMs fail to generate functional complex kernels for Ascend NPUs, yielding a near-zero success rate. To address these challenges, we propose AscendKernelGen, a generation-evaluation integrated framework for NPU kernel development. We introduce Ascend-CoT, a high-quality dataset incorporating chain-of-thought reasoning derived from real-world kernel implementations, and KernelGen-LM, a domain-adaptive model trained via supervised fine-tuning and reinforcement learning with execution feedback. Furthermore, we design NPUKernelBench, a comprehensive benchmark for assessing compilation, correctness, and performance across varying complexity levels. Experimental results demonstrate that our approach significantly bridges the gap between general LLMs and hardware-specific coding. Specifically, the compilation success rate on complex Level-2 kernels improves from 0% to 95.5% (Pass@10), while functional correctness achieves 64.3% compared to the baseline's complete failure. These results highlight the critical role of domain-specific reasoning and rigorous evaluation in automating accelerator-aware code generation.

Efficient Event Stream Super-Resolution with Recursive Multi-Branch Fusion

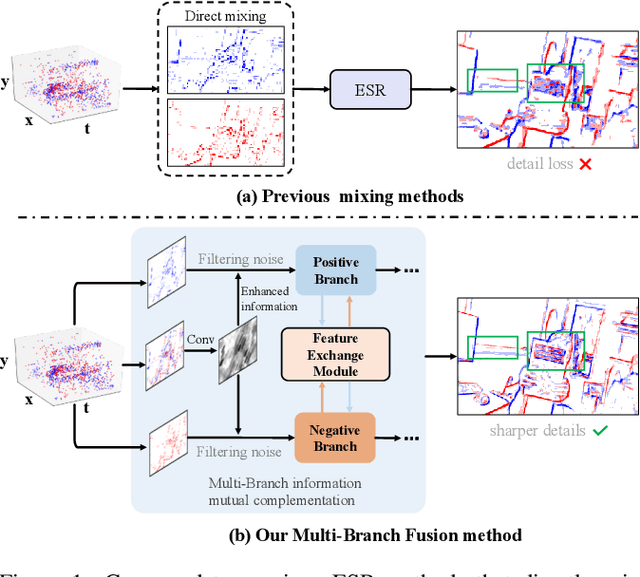
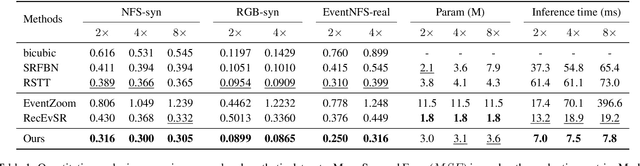
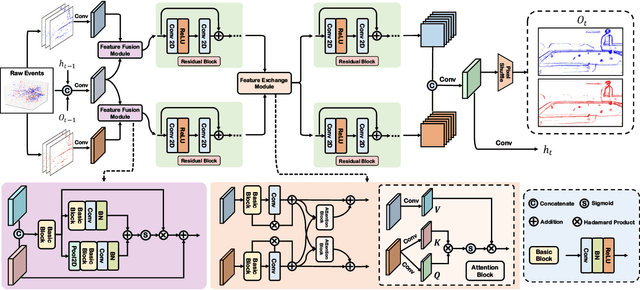
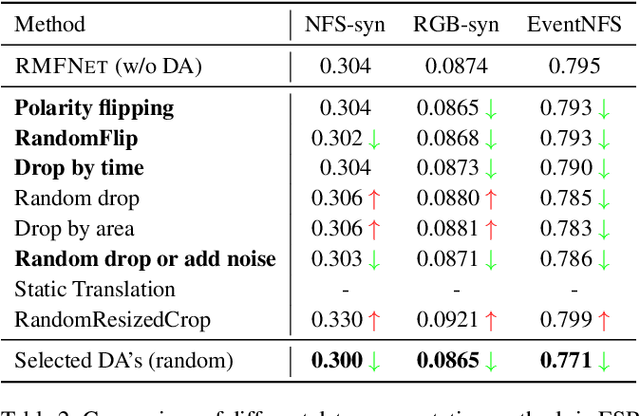
Current Event Stream Super-Resolution (ESR) methods overlook the redundant and complementary information present in positive and negative events within the event stream, employing a direct mixing approach for super-resolution, which may lead to detail loss and inefficiency. To address these issues, we propose an efficient Recursive Multi-Branch Information Fusion Network (RMFNet) that separates positive and negative events for complementary information extraction, followed by mutual supplementation and refinement. Particularly, we introduce Feature Fusion Modules (FFM) and Feature Exchange Modules (FEM). FFM is designed for the fusion of contextual information within neighboring event streams, leveraging the coupling relationship between positive and negative events to alleviate the misleading of noises in the respective branches. FEM efficiently promotes the fusion and exchange of information between positive and negative branches, enabling superior local information enhancement and global information complementation. Experimental results demonstrate that our approach achieves over 17% and 31% improvement on synthetic and real datasets, accompanied by a 2.3X acceleration. Furthermore, we evaluate our method on two downstream event-driven applications, \emph{i.e.}, object recognition and video reconstruction, achieving remarkable results that outperform existing methods. Our code and Supplementary Material are available at https://github.com/Lqm26/RMFNet.

Online Convex Optimization with Classical and Quantum Evaluation Oracles

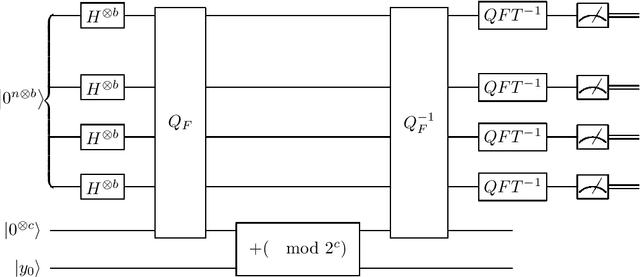
As a fundamental tool in AI, convex optimization has been a significant research field for many years, and the same goes for its online version. Recently, general convex optimization problem has been accelerated with the help of quantum computing, and the technique of online convex optimization has been used for accelerating the online quantum state learning problem, thus we want to study whether online convex optimization (OCO) model can also be benefited from quantum computing. In this paper, we consider the OCO model, which can be described as a $T$ round iterative game between the player and the adversary. A key factor for measuring the performance of an OCO algorithm ${\cal A}$ is the regret denoted by $\text{regret}_{T}(\mathcal{A})$, and it is said to perform well if its regret is sublinear as a function of $T$. Another factor is the computational cost (e.g., query complexity) of the algorithm. We give a quantum algorithm for the online convex optimization model with only zeroth-order oracle available, which can achieve $O(\sqrt{T})$ and $O(\log{T})$ regret for general convex loss functions and $\alpha$-strong loss functions respectively, where only $O(1)$ queries are needed in each round. Our results show that the zeroth-order quantum oracle is as powerful as the classical first-order oracle, and show potential advantages of quantum computing over classical computing in the OCO model where only zeroth-order oracle available.