Enabling surrogate-assisted evolutionary reinforcement learning via policy embedding

Evolutionary Reinforcement Learning (ERL) that applying Evolutionary Algorithms (EAs) to optimize the weight parameters of Deep Neural Network (DNN) based policies has been widely regarded as an alternative to traditional reinforcement learning methods. However, the evaluation of the iteratively generated population usually requires a large amount of computational time and can be prohibitively expensive, which may potentially restrict the applicability of ERL. Surrogate is often used to reduce the computational burden of evaluation in EAs. Unfortunately, in ERL, each individual of policy usually represents millions of weights parameters of DNN. This high-dimensional representation of policy has introduced a great challenge to the application of surrogates into ERL to speed up training. This paper proposes a PE-SAERL Framework to at the first time enable surrogate-assisted evolutionary reinforcement learning via policy embedding (PE). Empirical results on 5 Atari games show that the proposed method can perform more efficiently than the four state-of-the-art algorithms. The training process is accelerated up to 7x on tested games, comparing to its counterpart without the surrogate and PE.

Analyzing the Weighted Nuclear Norm Minimization and Nuclear Norm Minimization based on Group Sparse Representation

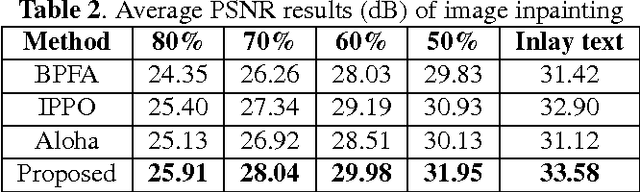
Rank minimization methods have attracted considerable interest in various areas, such as computer vision and machine learning. The most representative work is nuclear norm minimization (NNM), which can recover the matrix rank exactly under some restricted and theoretical guarantee conditions. However, for many real applications, NNM is not able to approximate the matrix rank accurately, since it often tends to over-shrink the rank components. To rectify the weakness of NNM, recent advances have shown that weighted nuclear norm minimization (WNNM) can achieve a better matrix rank approximation than NNM, which heuristically set the weight being inverse to the singular values. However, it still lacks a sound mathematical explanation on why WNNM is more feasible than NNM. In this paper, we propose a scheme to analyze WNNM and NNM from the perspective of the group sparse representation. Specifically, we design an adaptive dictionary to bridge the gap between the group sparse representation and the rank minimization models. Based on this scheme, we provide a mathematical derivation to explain why WNNM is more feasible than NNM. Moreover, due to the heuristical set of the weight, WNNM sometimes pops out error in the operation of SVD, and thus we present an adaptive weight setting scheme to avoid this error. We then employ the proposed scheme on two low-level vision tasks including image denoising and image inpainting. Experimental results demonstrate that WNNM is more feasible than NNM and the proposed scheme outperforms many current state-of-the-art methods.

Group Sparsity Residual with Non-Local Samples for Image Denoising

Inspired by group-based sparse coding, recently proposed group sparsity residual (GSR) scheme has demonstrated superior performance in image processing. However, one challenge in GSR is to estimate the residual by using a proper reference of the group-based sparse coding (GSC), which is desired to be as close to the truth as possible. Previous researches utilized the estimations from other algorithms (i.e., GMM or BM3D), which are either not accurate or too slow. In this paper, we propose to use the Non-Local Samples (NLS) as reference in the GSR regime for image denoising, thus termed GSR-NLS. More specifically, we first obtain a good estimation of the group sparse coefficients by the image nonlocal self-similarity, and then solve the GSR model by an effective iterative shrinkage algorithm. Experimental results demonstrate that the proposed GSR-NLS not only outperforms many state-of-the-art methods, but also delivers the competitive advantage of speed.

Group-based Sparse Representation for Image Compressive Sensing Reconstruction with Non-Convex Regularization

Patch-based sparse representation modeling has shown great potential in image compressive sensing (CS) reconstruction. However, this model usually suffers from some limits, such as dictionary learning with great computational complexity, neglecting the relationship among similar patches. In this paper, a group-based sparse representation method with non-convex regularization (GSR-NCR) for image CS reconstruction is proposed. In GSR-NCR, the local sparsity and nonlocal self-similarity of images is simultaneously considered in a unified framework. Different from the previous methods based on sparsity-promoting convex regularization, we extend the non-convex weighted Lp (0 < p < 1) penalty function on group sparse coefficients of the data matrix, rather than conventional L1-based regularization. To reduce the computational complexity, instead of learning the dictionary with a high computational complexity from natural images, we learn the principle component analysis (PCA) based dictionary for each group. Moreover, to make the proposed scheme tractable and robust, we have developed an efficient iterative shrinkage/thresholding algorithm to solve the non-convex optimization problem. Experimental results demonstrate that the proposed method outperforms many state-of-the-art techniques for image CS reconstruction.

Group Sparsity Residual Constraint for Image Denoising

Group-based sparse representation has shown great potential in image denoising. However, most existing methods only consider the nonlocal self-similarity (NSS) prior of noisy input image. That is, the similar patches are collected only from degraded input, which makes the quality of image denoising largely depend on the input itself. However, such methods often suffer from a common drawback that the denoising performance may degrade quickly with increasing noise levels. In this paper we propose a new prior model, called group sparsity residual constraint (GSRC). Unlike the conventional group-based sparse representation denoising methods, two kinds of prior, namely, the NSS priors of noisy and pre-filtered images, are used in GSRC. In particular, we integrate these two NSS priors through the mechanism of sparsity residual, and thus, the task of image denoising is converted to the problem of reducing the group sparsity residual. To this end, we first obtain a good estimation of the group sparse coefficients of the original image by pre-filtering, and then the group sparse coefficients of the noisy image are used to approximate this estimation. To improve the accuracy of the nonlocal similar patch selection, an adaptive patch search scheme is designed. Furthermore, to fuse these two NSS prior better, an effective iterative shrinkage algorithm is developed to solve the proposed GSRC model. Experimental results demonstrate that the proposed GSRC modeling outperforms many state-of-the-art denoising methods in terms of the objective and the perceptual metrics.

Non-Convex Weighted Lp Nuclear Norm based ADMM Framework for Image Restoration

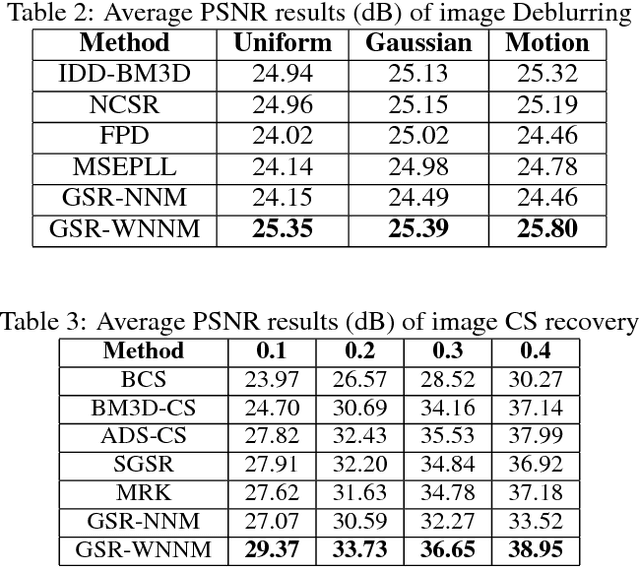
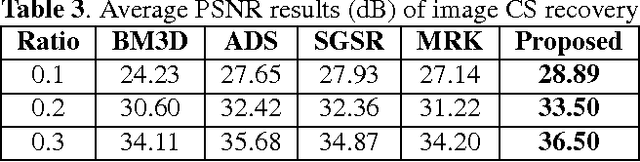
Since the matrix formed by nonlocal similar patches in a natural image is of low rank, the nuclear norm minimization (NNM) has been widely used in various image processing studies. Nonetheless, nuclear norm based convex surrogate of the rank function usually over-shrinks the rank components and makes different components equally, and thus may produce a result far from the optimum. To alleviate the above-mentioned limitations of the nuclear norm, in this paper we propose a new method for image restoration via the non-convex weighted Lp nuclear norm minimization (NCW-NNM), which is able to more accurately enforce the image structural sparsity and self-similarity simultaneously. To make the proposed model tractable and robust, the alternative direction multiplier method (ADMM) is adopted to solve the associated non-convex minimization problem. Experimental results on various types of image restoration problems, including image deblurring, image inpainting and image compressive sensing (CS) recovery, demonstrate that the proposed method outperforms many current state-of-the-art methods in both the objective and the perceptual qualities.

Analyzing the group sparsity based on the rank minimization methods

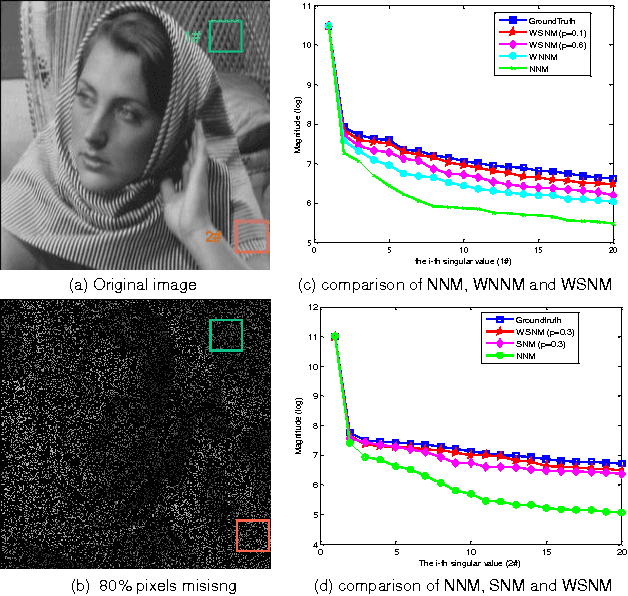
Sparse coding has achieved a great success in various image processing studies. However, there is not any benchmark to measure the sparsity of image patch/group because sparse discriminant conditions cannot keep unchanged. This paper analyzes the sparsity of group based on the strategy of the rank minimization. Firstly, an adaptive dictionary for each group is designed. Then, we prove that group-based sparse coding is equivalent to the rank minimization problem, and thus the sparse coefficient of each group is measured by estimating the singular values of each group. Based on that measurement, the weighted Schatten $p$-norm minimization (WSNM) has been found to be the closest solution to the real singular values of each group. Thus, WSNM can be equivalently transformed into a non-convex $\ell_p$-norm minimization problem in group-based sparse coding. To make the proposed scheme tractable and robust, the alternating direction method of multipliers (ADMM) is used to solve the $\ell_p$-norm minimization problem. Experimental results on two applications: image inpainting and image compressive sensing (CS) recovery have shown that the proposed scheme outperforms many state-of-the-art methods.

Non-Convex Weighted Lp Minimization based Group Sparse Representation Framework for Image Denoising

Nonlocal image representation or group sparsity has attracted considerable interest in various low-level vision tasks and has led to several state-of-the-art image denoising techniques, such as BM3D, LSSC. In the past, convex optimization with sparsity-promoting convex regularization was usually regarded as a standard scheme for estimating sparse signals in noise. However, using convex regularization can not still obtain the correct sparsity solution under some practical problems including image inverse problems. In this paper we propose a non-convex weighted $\ell_p$ minimization based group sparse representation (GSR) framework for image denoising. To make the proposed scheme tractable and robust, the generalized soft-thresholding (GST) algorithm is adopted to solve the non-convex $\ell_p$ minimization problem. In addition, to improve the accuracy of the nonlocal similar patches selection, an adaptive patch search (APS) scheme is proposed. Experimental results have demonstrated that the proposed approach not only outperforms many state-of-the-art denoising methods such as BM3D and WNNM, but also results in a competitive speed.

A Comparative Study for the Weighted Nuclear Norm Minimization and Nuclear Norm Minimization

Nuclear norm minimization (NNM) tends to over-shrink the rank components and treats the different rank components equally, thus limits its capability and flexibility. Recent studies have shown that the weighted nuclear norm minimization (WNNM) is expected to be more accurate than NNM. However, it still lacks a plausible mathematical explanation why WNNM is more accurate than NNM. This paper analyzes the WNNM and NNM from the perspective of the group sparse representation (GSR). In particular, an adaptive dictionary for each group is designed to connect the rank minimization and GSR models. Then, we prove that the rank minimization model is equivalent to GSR model. Based on that conclusion, we show mathematically that WNNM is more accurate than NNM. To make the proposed model tractable and robust, the alternative direction multiplier method (ADMM) framework is developed to solve the proposed model. We exploit the proposed scheme to three low level vision tasks, including image deblurring, image inpainting and image compressive sensing (CS) recovery. Experimental results demonstrate that the proposed scheme outperforms many state-of-the-art methods in terms of both quantitative measures and visual perception quality.

Image denoising via group sparsity residual constraint

Group sparsity has shown great potential in various low-level vision tasks (e.g, image denoising, deblurring and inpainting). In this paper, we propose a new prior model for image denoising via group sparsity residual constraint (GSRC). To enhance the performance of group sparse-based image denoising, the concept of group sparsity residual is proposed, and thus, the problem of image denoising is translated into one that reduces the group sparsity residual. To reduce the residual, we first obtain some good estimation of the group sparse coefficients of the original image by the first-pass estimation of noisy image, and then centralize the group sparse coefficients of noisy image to the estimation. Experimental results have demonstrated that the proposed method not only outperforms many state-of-the-art denoising methods such as BM3D and WNNM, but results in a faster speed.