Analyzing the group sparsity based on the rank minimization methods
Paper and Code
Jun 12, 2017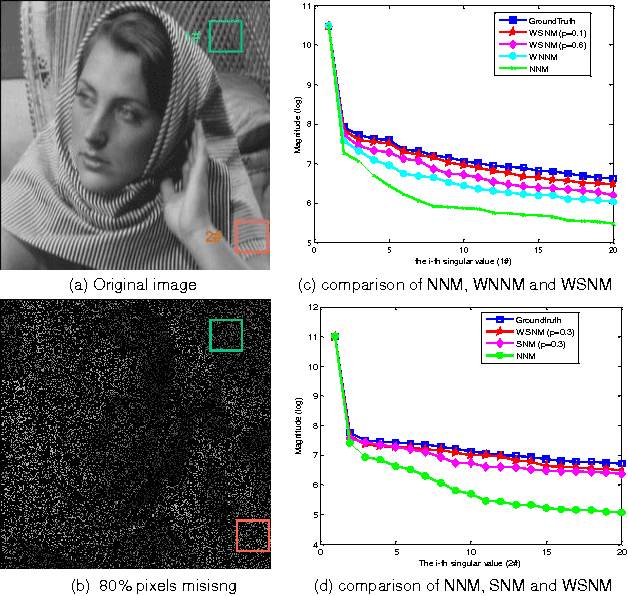
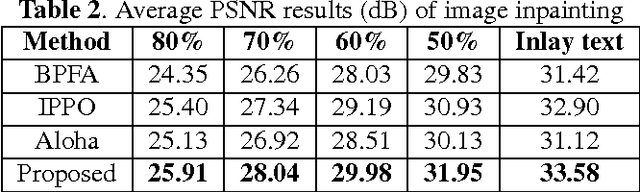

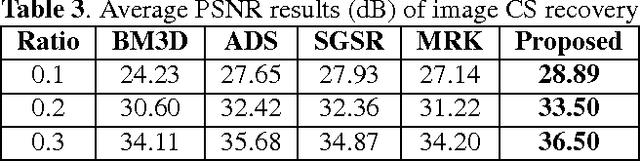
Sparse coding has achieved a great success in various image processing studies. However, there is not any benchmark to measure the sparsity of image patch/group because sparse discriminant conditions cannot keep unchanged. This paper analyzes the sparsity of group based on the strategy of the rank minimization. Firstly, an adaptive dictionary for each group is designed. Then, we prove that group-based sparse coding is equivalent to the rank minimization problem, and thus the sparse coefficient of each group is measured by estimating the singular values of each group. Based on that measurement, the weighted Schatten $p$-norm minimization (WSNM) has been found to be the closest solution to the real singular values of each group. Thus, WSNM can be equivalently transformed into a non-convex $\ell_p$-norm minimization problem in group-based sparse coding. To make the proposed scheme tractable and robust, the alternating direction method of multipliers (ADMM) is used to solve the $\ell_p$-norm minimization problem. Experimental results on two applications: image inpainting and image compressive sensing (CS) recovery have shown that the proposed scheme outperforms many state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge