Kumara Sastry
An Adversarial Active Sampling-based Data Augmentation Framework for Manufacturable Chip Design
Oct 27, 2022Abstract:Lithography modeling is a crucial problem in chip design to ensure a chip design mask is manufacturable. It requires rigorous simulations of optical and chemical models that are computationally expensive. Recent developments in machine learning have provided alternative solutions in replacing the time-consuming lithography simulations with deep neural networks. However, the considerable accuracy drop still impedes its industrial adoption. Most importantly, the quality and quantity of the training dataset directly affect the model performance. To tackle this problem, we propose a litho-aware data augmentation (LADA) framework to resolve the dilemma of limited data and improve the machine learning model performance. First, we pretrain the neural networks for lithography modeling and a gradient-friendly StyleGAN2 generator. We then perform adversarial active sampling to generate informative and synthetic in-distribution mask designs. These synthetic mask images will augment the original limited training dataset used to finetune the lithography model for improved performance. Experimental results demonstrate that LADA can successfully exploits the neural network capacity by narrowing down the performance gap between the training and testing data instances.
Large Scale Mask Optimization Via Convolutional Fourier Neural Operator and Litho-Guided Self Training
Jul 08, 2022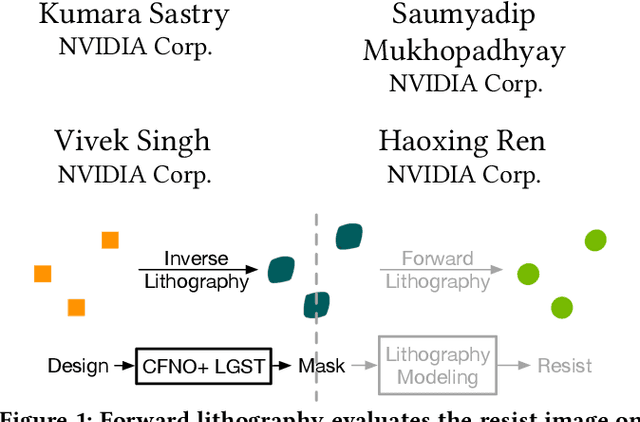
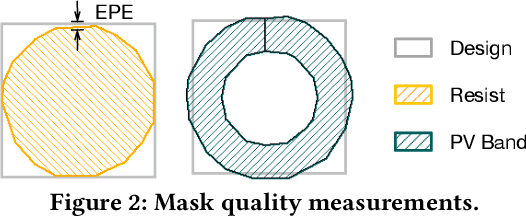
Abstract:Machine learning techniques have been extensively studied for mask optimization problems, aiming at better mask printability, shorter turnaround time, better mask manufacturability, and so on. However, most of these researches are focusing on the initial solution generation of small design regions. To further realize the potential of machine learning techniques on mask optimization tasks, we present a Convolutional Fourier Neural Operator (CFNO) that can efficiently learn layout tile dependencies and hence promise stitch-less large-scale mask optimization with the limited intervention of legacy tools. We discover the possibility of litho-guided self-training (LGST) through a trained machine learning model when solving non-convex optimization problems, which allows iterative model and dataset update and brings significant model performance improvement. Experimental results show that, for the first time, our machine learning-based framework outperforms state-of-the-art academic numerical mask optimizers with an order of magnitude speedup.
Generic Lithography Modeling with Dual-band Optics-Inspired Neural Networks
Mar 12, 2022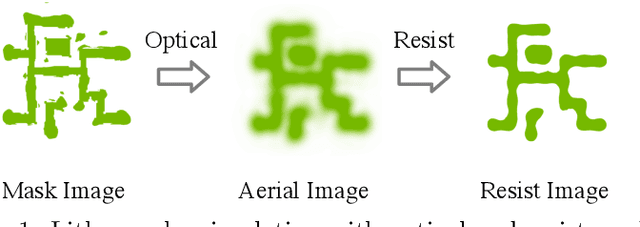

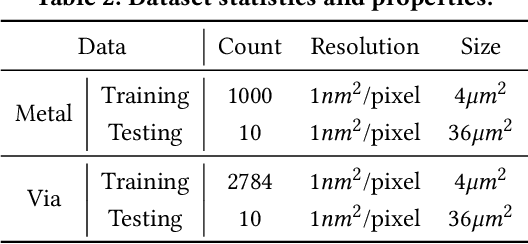
Abstract:Lithography simulation is a critical step in VLSI design and optimization for manufacturability. Existing solutions for highly accurate lithography simulation with rigorous models are computationally expensive and slow, even when equipped with various approximation techniques. Recently, machine learning has provided alternative solutions for lithography simulation tasks such as coarse-grained edge placement error regression and complete contour prediction. However, the impact of these learning-based methods has been limited due to restrictive usage scenarios or low simulation accuracy. To tackle these concerns, we introduce an dual-band optics-inspired neural network design that considers the optical physics underlying lithography. To the best of our knowledge, our approach yields the first published via/metal layer contour simulation at 1nm^2/pixel resolution with any tile size. Compared to previous machine learning based solutions, we demonstrate that our framework can be trained much faster and offers a significant improvement on efficiency and image quality with 20X smaller model size. We also achieve 85X simulation speedup over traditional lithography simulator with 1% accuracy loss.
iBOA: The Incremental Bayesian Optimization Algorithm
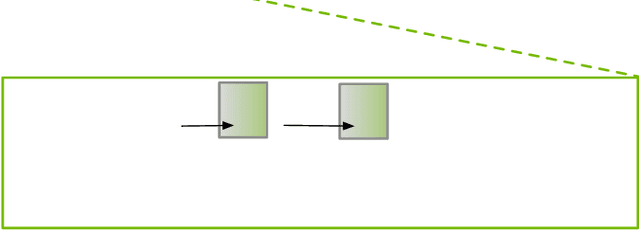
Jan 21, 2008
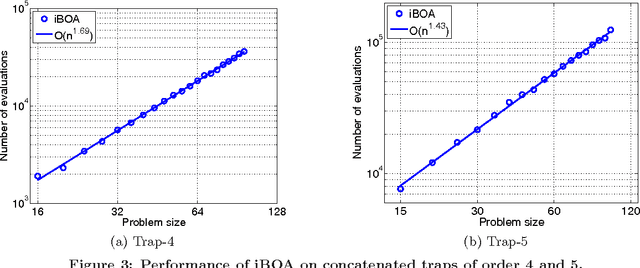
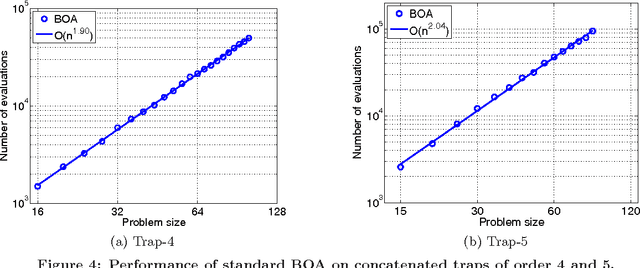
Abstract:This paper proposes the incremental Bayesian optimization algorithm (iBOA), which modifies standard BOA by removing the population of solutions and using incremental updates of the Bayesian network. iBOA is shown to be able to learn and exploit unrestricted Bayesian networks using incremental techniques for updating both the structure as well as the parameters of the probabilistic model. This represents an important step toward the design of competent incremental estimation of distribution algorithms that can solve difficult nearly decomposable problems scalably and reliably.
* Also available at the MEDAL web site, http://medal.cs.umsl.edu/
Decomposable Problems, Niching, and Scalability of Multiobjective Estimation of Distribution Algorithms
Feb 12, 2005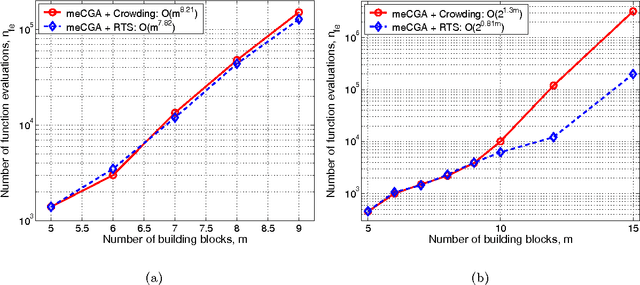

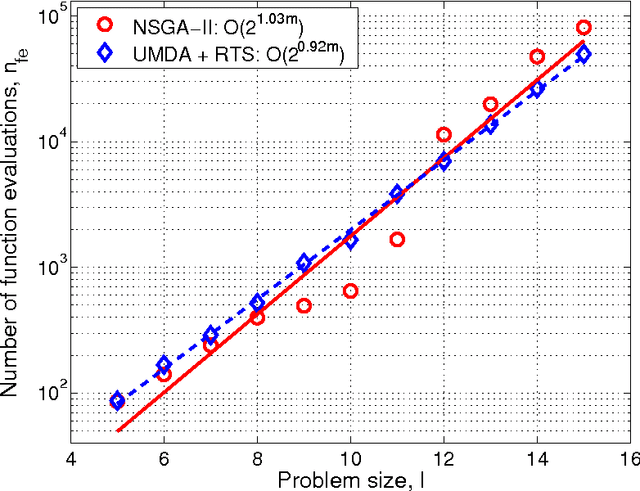
Abstract:The paper analyzes the scalability of multiobjective estimation of distribution algorithms (MOEDAs) on a class of boundedly-difficult additively-separable multiobjective optimization problems. The paper illustrates that even if the linkage is correctly identified, massive multimodality of the search problems can easily overwhelm the nicher and lead to exponential scale-up. Facetwise models are subsequently used to propose a growth rate of the number of differing substructures between the two objectives to avoid the niching method from being overwhelmed and lead to polynomial scalability of MOEDAs.
Scalability of Genetic Programming and Probabilistic Incremental Program Evolution
Feb 07, 2005


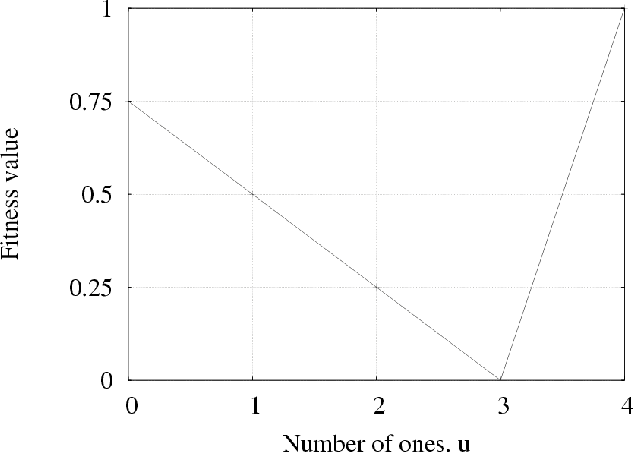
Abstract:This paper discusses scalability of standard genetic programming (GP) and the probabilistic incremental program evolution (PIPE). To investigate the need for both effective mixing and linkage learning, two test problems are considered: ORDER problem, which is rather easy for any recombination-based GP, and TRAP or the deceptive trap problem, which requires the algorithm to learn interactions among subsets of terminals. The scalability results show that both GP and PIPE scale up polynomially with problem size on the simple ORDER problem, but they both scale up exponentially on the deceptive problem. This indicates that while standard recombination is sufficient when no interactions need to be considered, for some problems linkage learning is necessary. These results are in agreement with the lessons learned in the domain of binary-string genetic algorithms (GAs). Furthermore, the paper investigates the effects of introducing utnnecessary and irrelevant primitives on the performance of GP and PIPE.
Multiobjective hBOA, Clustering, and Scalability
Feb 07, 2005

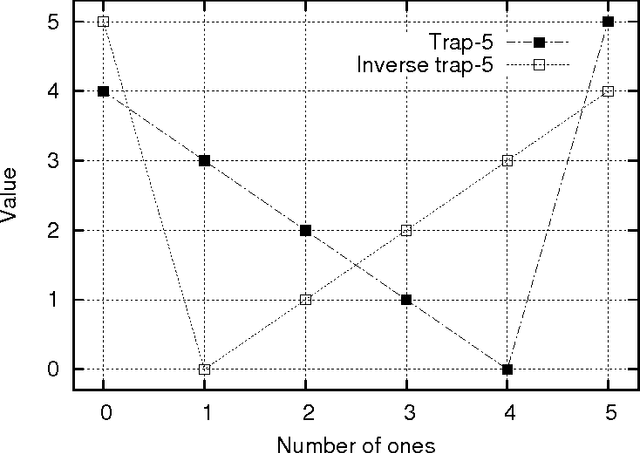
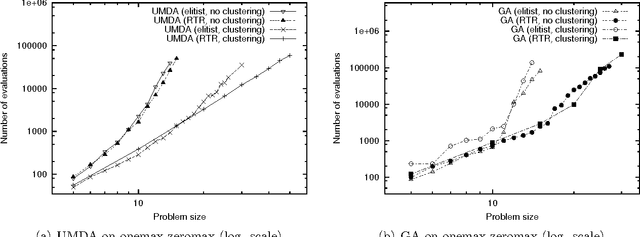
Abstract:This paper describes a scalable algorithm for solving multiobjective decomposable problems by combining the hierarchical Bayesian optimization algorithm (hBOA) with the nondominated sorting genetic algorithm (NSGA-II) and clustering in the objective space. It is first argued that for good scalability, clustering or some other form of niching in the objective space is necessary and the size of each niche should be approximately equal. Multiobjective hBOA (mohBOA) is then described that combines hBOA, NSGA-II and clustering in the objective space. The algorithm mohBOA differs from the multiobjective variants of BOA and hBOA proposed in the past by including clustering in the objective space and allocating an approximately equally sized portion of the population to each cluster. The algorithm mohBOA is shown to scale up well on a number of problems on which standard multiobjective evolutionary algorithms perform poorly.
Efficiency Enhancement of Genetic Algorithms via Building-Block-Wise Fitness Estimation
May 18, 2004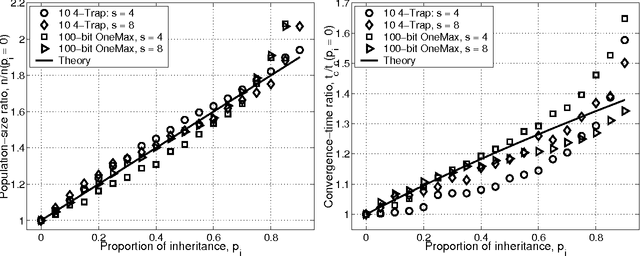
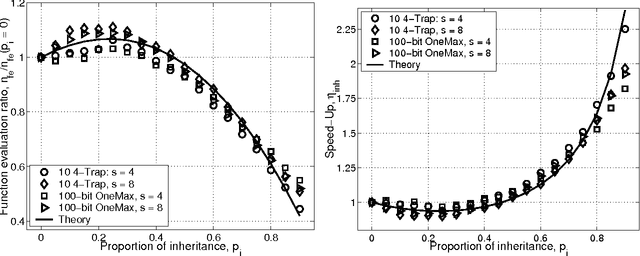
Abstract:This paper studies fitness inheritance as an efficiency enhancement technique for a class of competent genetic algorithms called estimation distribution algorithms. Probabilistic models of important sub-solutions are developed to estimate the fitness of a proportion of individuals in the population, thereby avoiding computationally expensive function evaluations. The effect of fitness inheritance on the convergence time and population sizing are modeled and the speed-up obtained through inheritance is predicted. The results show that a fitness-inheritance mechanism which utilizes information on building-block fitnesses provides significant efficiency enhancement. For additively separable problems, fitness inheritance reduces the number of function evaluations to about half and yields a speed-up of about 1.75--2.25.
Designing Competent Mutation Operators via Probabilistic Model Building of Neighborhoods
May 18, 2004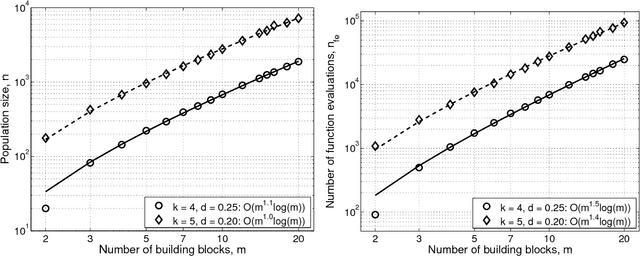
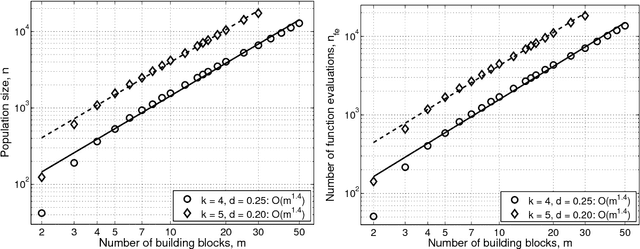
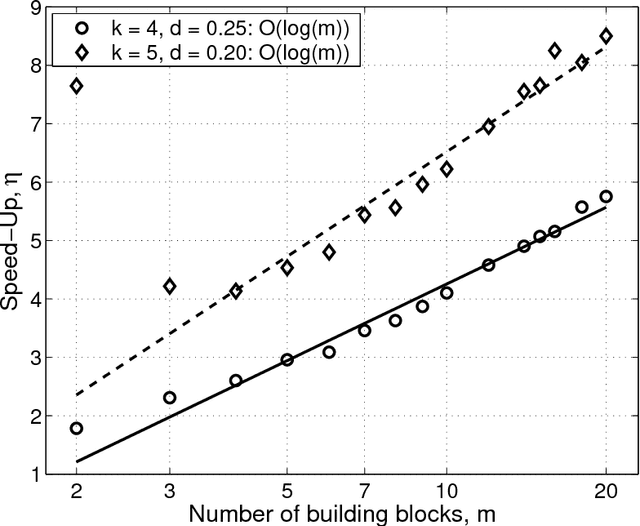
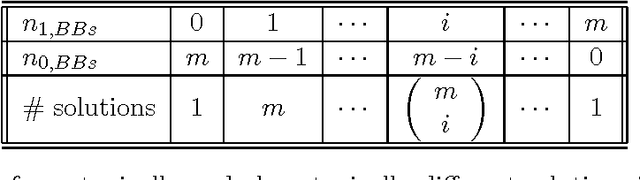
Abstract:This paper presents a competent selectomutative genetic algorithm (GA), that adapts linkage and solves hard problems quickly, reliably, and accurately. A probabilistic model building process is used to automatically identify key building blocks (BBs) of the search problem. The mutation operator uses the probabilistic model of linkage groups to find the best among competing building blocks. The competent selectomutative GA successfully solves additively separable problems of bounded difficulty, requiring only subquadratic number of function evaluations. The results show that for additively separable problems the probabilistic model building BB-wise mutation scales as O(2^km^{1.5}), and requires O(k^{0.5}logm) less function evaluations than its selectorecombinative counterpart, confirming theoretical results reported elsewhere (Sastry & Goldberg, 2004).
Let's Get Ready to Rumble: Crossover Versus Mutation Head to Head
May 18, 2004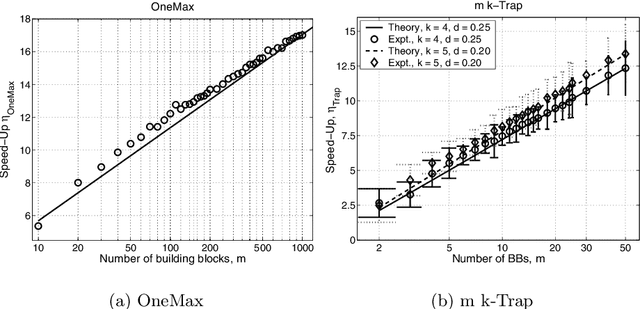

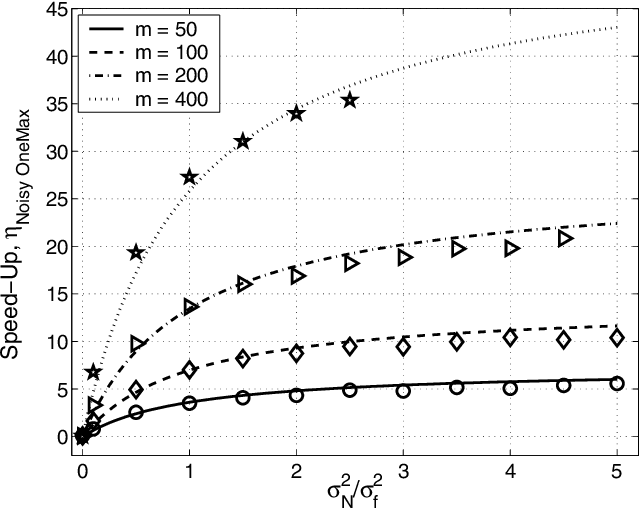
Abstract:This paper analyzes the relative advantages between crossover and mutation on a class of deterministic and stochastic additively separable problems. This study assumes that the recombination and mutation operators have the knowledge of the building blocks (BBs) and effectively exchange or search among competing BBs. Facetwise models of convergence time and population sizing have been used to determine the scalability of each algorithm. The analysis shows that for additively separable deterministic problems, the BB-wise mutation is more efficient than crossover, while the crossover outperforms the mutation on additively separable problems perturbed with additive Gaussian noise. The results show that the speed-up of using BB-wise mutation on deterministic problems is O(k^{0.5}logm), where k is the BB size, and m is the number of BBs. Likewise, the speed-up of using crossover on stochastic problems with fixed noise variance is O(mk^{0.5}log m).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge