iBOA: The Incremental Bayesian Optimization Algorithm

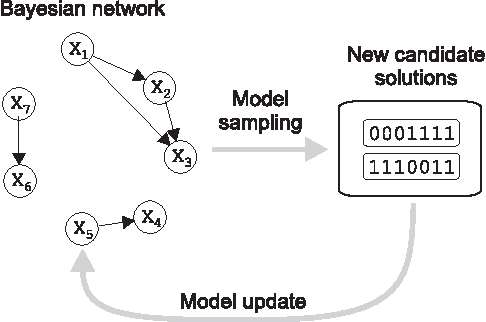
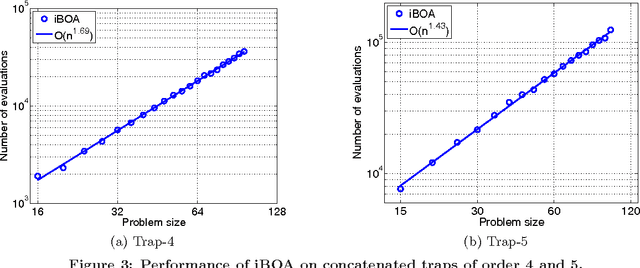
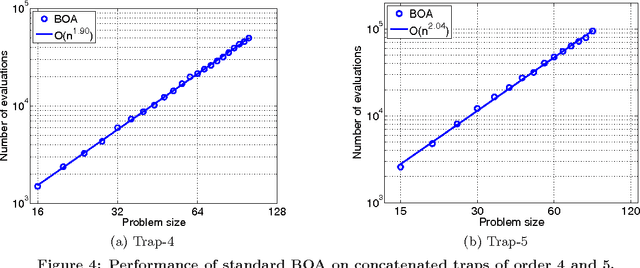
This paper proposes the incremental Bayesian optimization algorithm (iBOA), which modifies standard BOA by removing the population of solutions and using incremental updates of the Bayesian network. iBOA is shown to be able to learn and exploit unrestricted Bayesian networks using incremental techniques for updating both the structure as well as the parameters of the probabilistic model. This represents an important step toward the design of competent incremental estimation of distribution algorithms that can solve difficult nearly decomposable problems scalably and reliably.

Decomposable Problems, Niching, and Scalability of Multiobjective Estimation of Distribution Algorithms

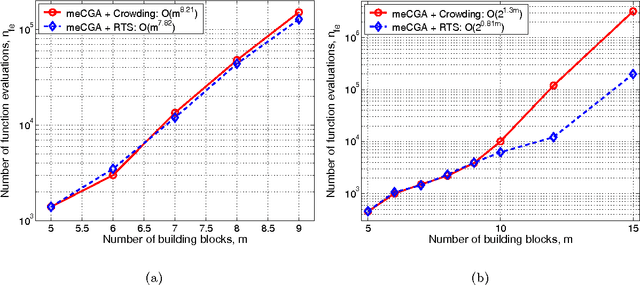
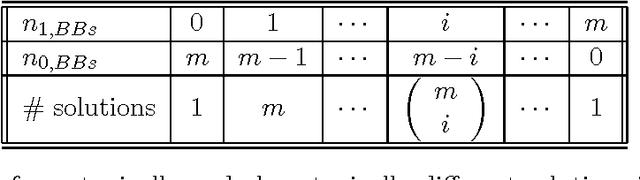
The paper analyzes the scalability of multiobjective estimation of distribution algorithms (MOEDAs) on a class of boundedly-difficult additively-separable multiobjective optimization problems. The paper illustrates that even if the linkage is correctly identified, massive multimodality of the search problems can easily overwhelm the nicher and lead to exponential scale-up. Facetwise models are subsequently used to propose a growth rate of the number of differing substructures between the two objectives to avoid the niching method from being overwhelmed and lead to polynomial scalability of MOEDAs.

Multiobjective hBOA, Clustering, and Scalability

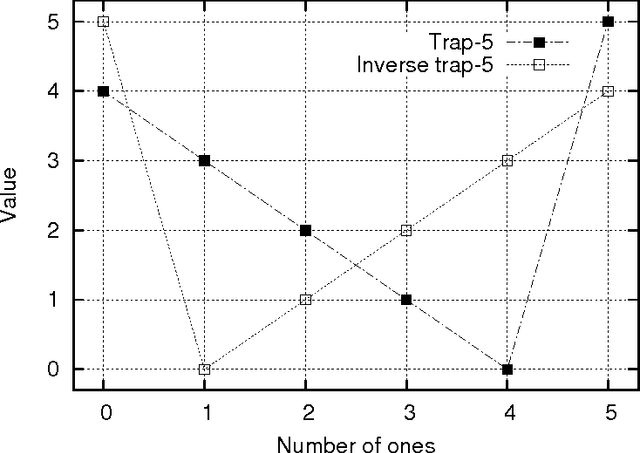
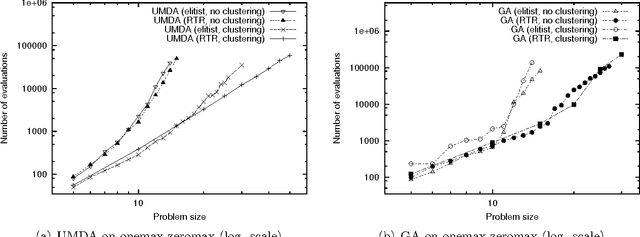
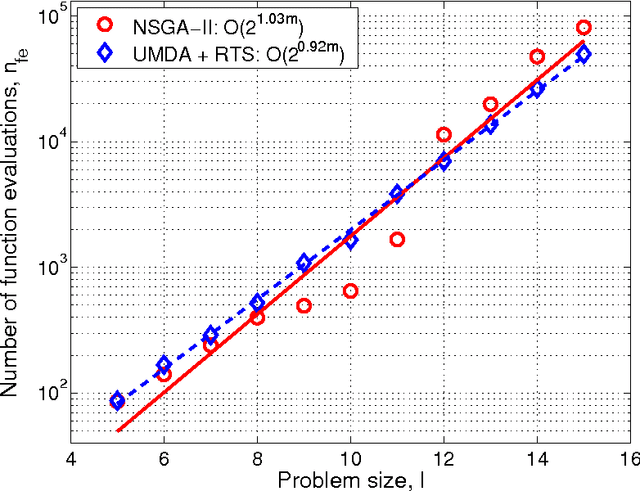
This paper describes a scalable algorithm for solving multiobjective decomposable problems by combining the hierarchical Bayesian optimization algorithm (hBOA) with the nondominated sorting genetic algorithm (NSGA-II) and clustering in the objective space. It is first argued that for good scalability, clustering or some other form of niching in the objective space is necessary and the size of each niche should be approximately equal. Multiobjective hBOA (mohBOA) is then described that combines hBOA, NSGA-II and clustering in the objective space. The algorithm mohBOA differs from the multiobjective variants of BOA and hBOA proposed in the past by including clustering in the objective space and allocating an approximately equally sized portion of the population to each cluster. The algorithm mohBOA is shown to scale up well on a number of problems on which standard multiobjective evolutionary algorithms perform poorly.

Efficiency Enhancement of Genetic Algorithms via Building-Block-Wise Fitness Estimation

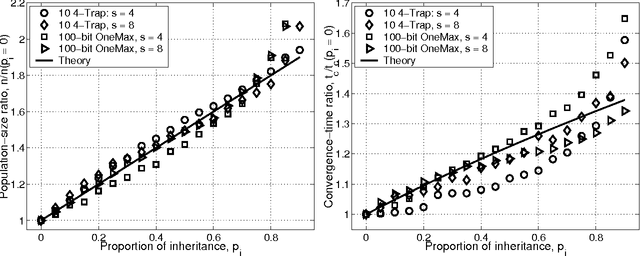
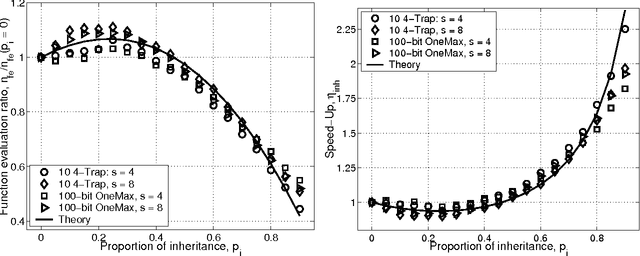
This paper studies fitness inheritance as an efficiency enhancement technique for a class of competent genetic algorithms called estimation distribution algorithms. Probabilistic models of important sub-solutions are developed to estimate the fitness of a proportion of individuals in the population, thereby avoiding computationally expensive function evaluations. The effect of fitness inheritance on the convergence time and population sizing are modeled and the speed-up obtained through inheritance is predicted. The results show that a fitness-inheritance mechanism which utilizes information on building-block fitnesses provides significant efficiency enhancement. For additively separable problems, fitness inheritance reduces the number of function evaluations to about half and yields a speed-up of about 1.75--2.25.

Designing Competent Mutation Operators via Probabilistic Model Building of Neighborhoods

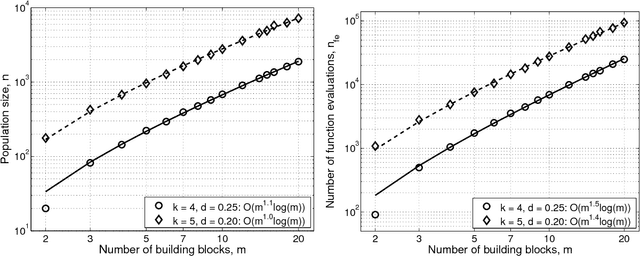
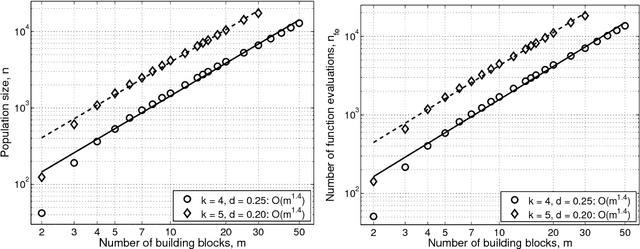
This paper presents a competent selectomutative genetic algorithm (GA), that adapts linkage and solves hard problems quickly, reliably, and accurately. A probabilistic model building process is used to automatically identify key building blocks (BBs) of the search problem. The mutation operator uses the probabilistic model of linkage groups to find the best among competing building blocks. The competent selectomutative GA successfully solves additively separable problems of bounded difficulty, requiring only subquadratic number of function evaluations. The results show that for additively separable problems the probabilistic model building BB-wise mutation scales as O(2^km^{1.5}), and requires O(k^{0.5}logm) less function evaluations than its selectorecombinative counterpart, confirming theoretical results reported elsewhere (Sastry & Goldberg, 2004).

Let's Get Ready to Rumble: Crossover Versus Mutation Head to Head

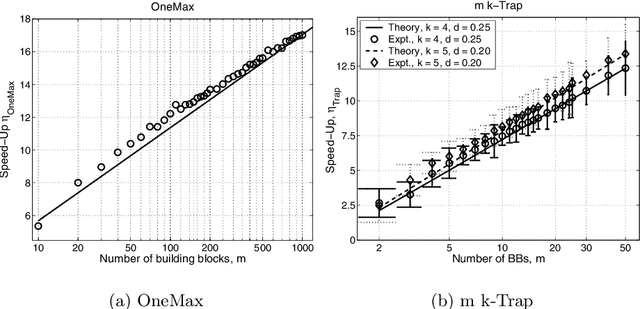
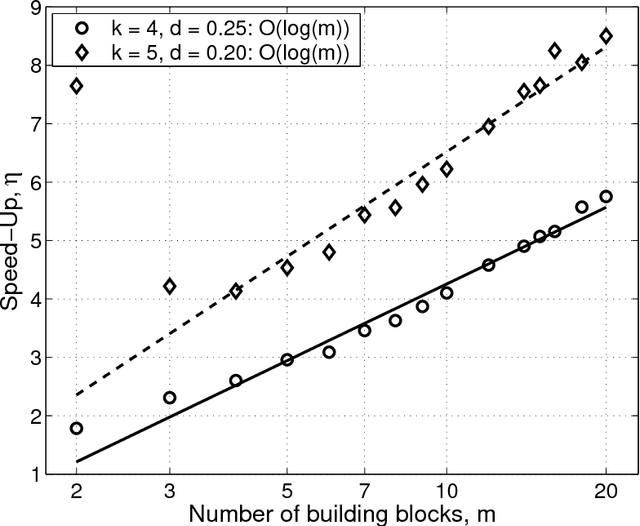
This paper analyzes the relative advantages between crossover and mutation on a class of deterministic and stochastic additively separable problems. This study assumes that the recombination and mutation operators have the knowledge of the building blocks (BBs) and effectively exchange or search among competing BBs. Facetwise models of convergence time and population sizing have been used to determine the scalability of each algorithm. The analysis shows that for additively separable deterministic problems, the BB-wise mutation is more efficient than crossover, while the crossover outperforms the mutation on additively separable problems perturbed with additive Gaussian noise. The results show that the speed-up of using BB-wise mutation on deterministic problems is O(k^{0.5}logm), where k is the BB size, and m is the number of BBs. Likewise, the speed-up of using crossover on stochastic problems with fixed noise variance is O(mk^{0.5}log m).

Efficiency Enhancement of Probabilistic Model Building Genetic Algorithms

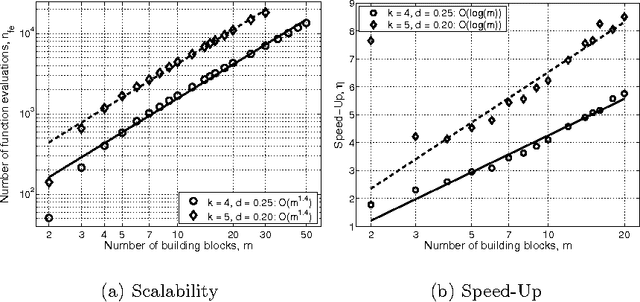
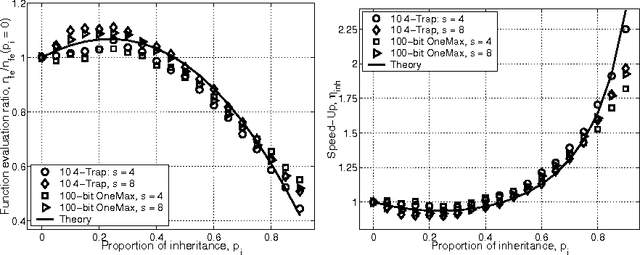
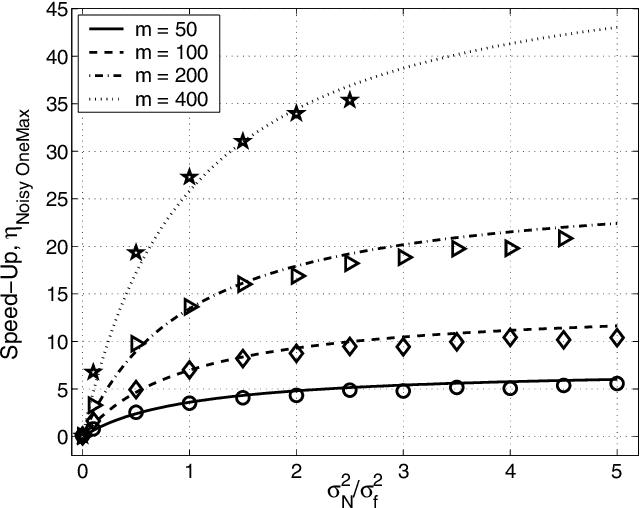
This paper presents two different efficiency-enhancement techniques for probabilistic model building genetic algorithms. The first technique proposes the use of a mutation operator which performs local search in the sub-solution neighborhood identified through the probabilistic model. The second technique proposes building and using an internal probabilistic model of the fitness along with the probabilistic model of variable interactions. The fitness values of some offspring are estimated using the probabilistic model, thereby avoiding computationally expensive function evaluations. The scalability of the aforementioned techniques are analyzed using facetwise models for convergence time and population sizing. The speed-up obtained by each of the methods is predicted and verified with empirical results. The results show that for additively separable problems the competent mutation operator requires O(k 0.5 logm)--where k is the building-block size, and m is the number of building blocks--less function evaluations than its selectorecombinative counterpart. The results also show that the use of an internal probabilistic fitness model reduces the required number of function evaluations to as low as 1-10% and yields a speed-up of 2--50.