Let's Get Ready to Rumble: Crossover Versus Mutation Head to Head
Paper and Code
May 18, 2004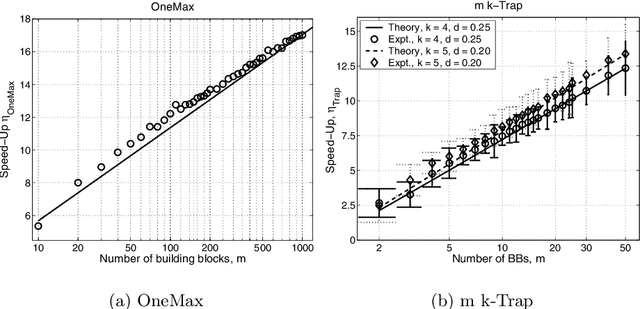

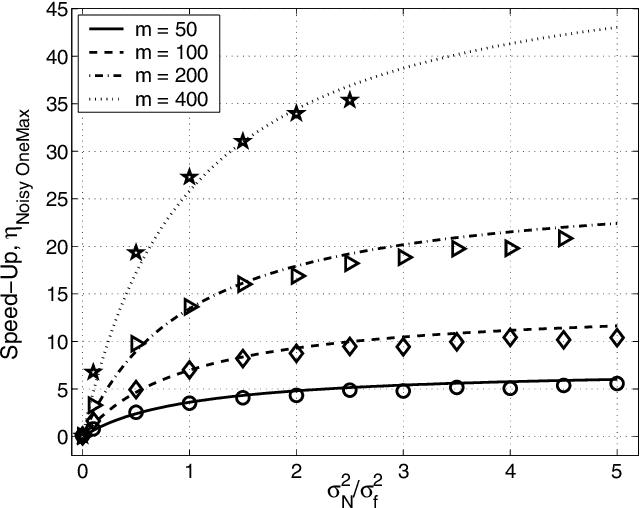
This paper analyzes the relative advantages between crossover and mutation on a class of deterministic and stochastic additively separable problems. This study assumes that the recombination and mutation operators have the knowledge of the building blocks (BBs) and effectively exchange or search among competing BBs. Facetwise models of convergence time and population sizing have been used to determine the scalability of each algorithm. The analysis shows that for additively separable deterministic problems, the BB-wise mutation is more efficient than crossover, while the crossover outperforms the mutation on additively separable problems perturbed with additive Gaussian noise. The results show that the speed-up of using BB-wise mutation on deterministic problems is O(k^{0.5}logm), where k is the BB size, and m is the number of BBs. Likewise, the speed-up of using crossover on stochastic problems with fixed noise variance is O(mk^{0.5}log m).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge