Designing Competent Mutation Operators via Probabilistic Model Building of Neighborhoods
Paper and Code
May 18, 2004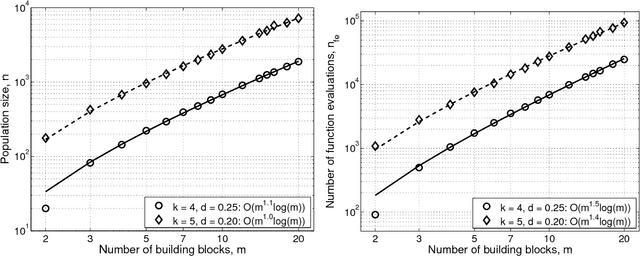
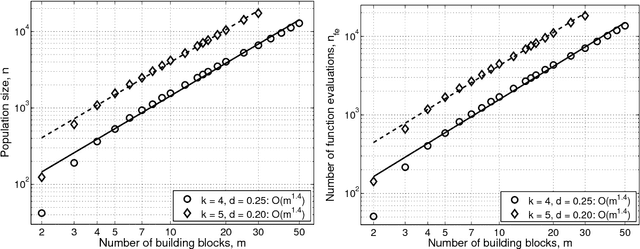
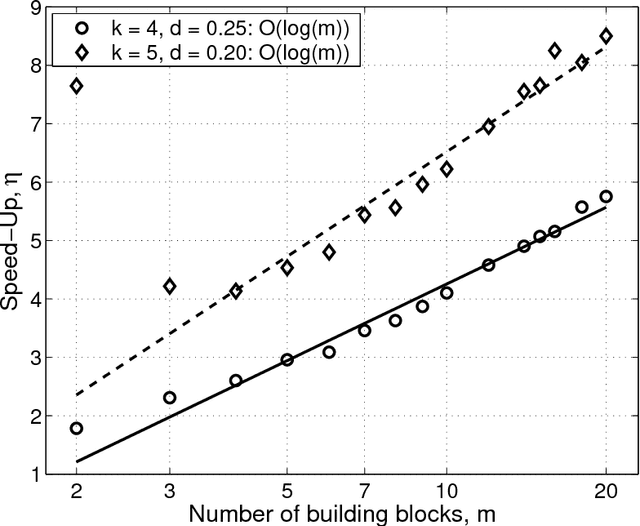
This paper presents a competent selectomutative genetic algorithm (GA), that adapts linkage and solves hard problems quickly, reliably, and accurately. A probabilistic model building process is used to automatically identify key building blocks (BBs) of the search problem. The mutation operator uses the probabilistic model of linkage groups to find the best among competing building blocks. The competent selectomutative GA successfully solves additively separable problems of bounded difficulty, requiring only subquadratic number of function evaluations. The results show that for additively separable problems the probabilistic model building BB-wise mutation scales as O(2^km^{1.5}), and requires O(k^{0.5}logm) less function evaluations than its selectorecombinative counterpart, confirming theoretical results reported elsewhere (Sastry & Goldberg, 2004).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge