Radovan Ondas
Scalability of Genetic Programming and Probabilistic Incremental Program Evolution
Feb 07, 2005


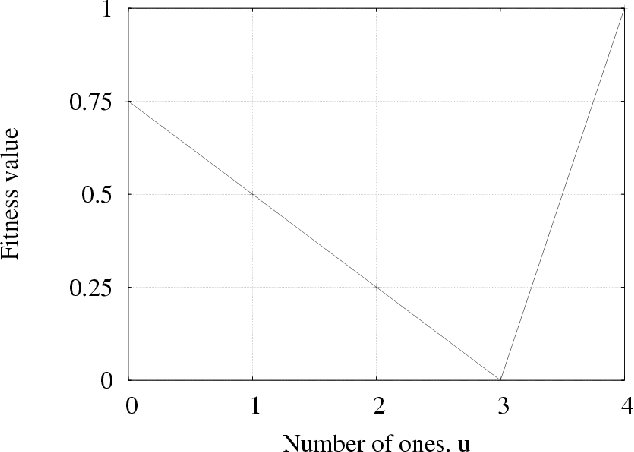
Abstract:This paper discusses scalability of standard genetic programming (GP) and the probabilistic incremental program evolution (PIPE). To investigate the need for both effective mixing and linkage learning, two test problems are considered: ORDER problem, which is rather easy for any recombination-based GP, and TRAP or the deceptive trap problem, which requires the algorithm to learn interactions among subsets of terminals. The scalability results show that both GP and PIPE scale up polynomially with problem size on the simple ORDER problem, but they both scale up exponentially on the deceptive problem. This indicates that while standard recombination is sufficient when no interactions need to be considered, for some problems linkage learning is necessary. These results are in agreement with the lessons learned in the domain of binary-string genetic algorithms (GAs). Furthermore, the paper investigates the effects of introducing utnnecessary and irrelevant primitives on the performance of GP and PIPE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge