Subspace Representation Learning for Sparse Linear Arrays to Localize More Sources than Sensors: A Deep Learning Methodology

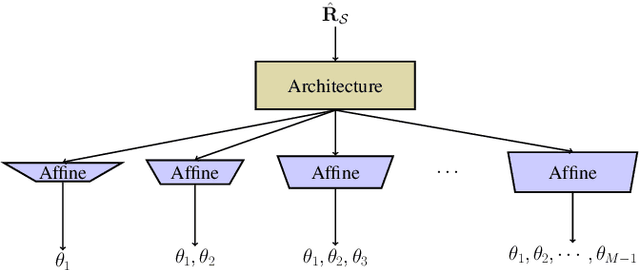
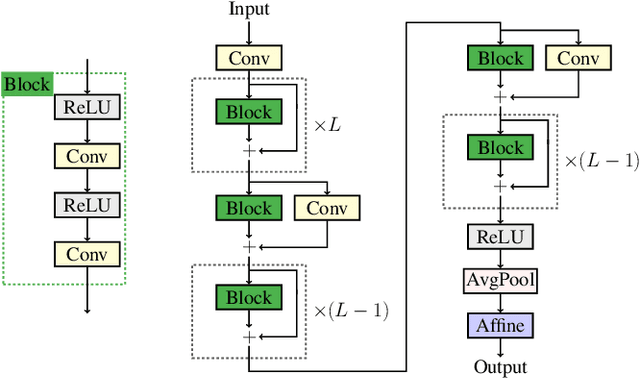
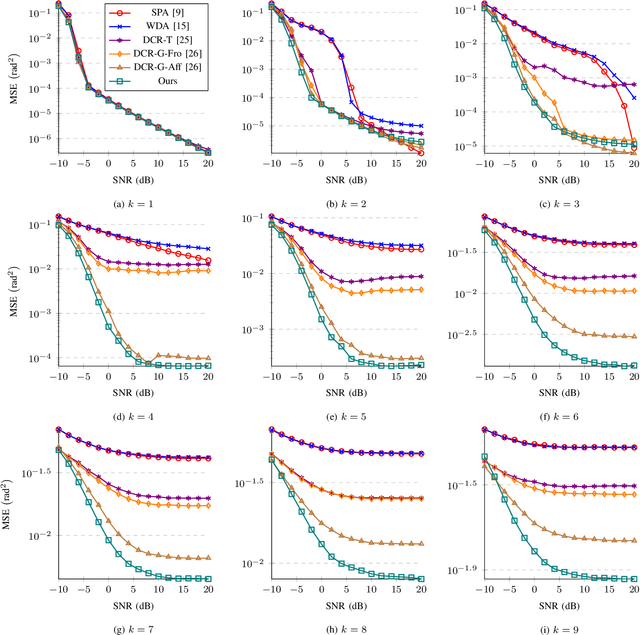
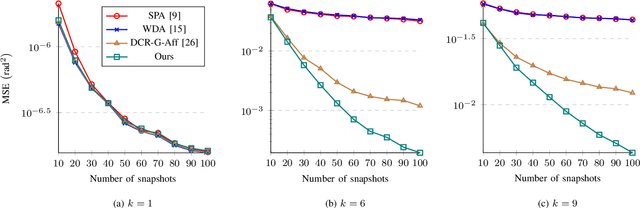
Localizing more sources than sensors with a sparse linear array (SLA) has long relied on minimizing a distance between two covariance matrices and recent algorithms often utilize semidefinite programming (SDP). Although deep neural network (DNN)-based methods offer new alternatives, they still depend on covariance matrix fitting. In this paper, we develop a novel methodology that estimates the co-array subspaces from a sample covariance for SLAs. Our methodology trains a DNN to learn signal and noise subspace representations that are invariant to the selection of bases. To learn such representations, we propose loss functions that gauge the separation between the desired and the estimated subspace. In particular, we propose losses that measure the length of the shortest path between subspaces viewed on a union of Grassmannians, and prove that it is possible for a DNN to approximate signal subspaces. The computation of learning subspaces of different dimensions is accelerated by a new batch sampling strategy called consistent rank sampling. The methodology is robust to array imperfections due to its geometry-agnostic and data-driven nature. In addition, we propose a fully end-to-end gridless approach that directly learns angles to study the possibility of bypassing subspace methods. Numerical results show that learning such subspace representations is more beneficial than learning covariances or angles. It outperforms conventional SDP-based methods such as the sparse and parametric approach (SPA) and existing DNN-based covariance reconstruction methods for a wide range of signal-to-noise ratios (SNRs), snapshots, and source numbers for both perfect and imperfect arrays.

A DNN based Normalized Time-frequency Weighted Criterion for Robust Wideband DoA Estimation

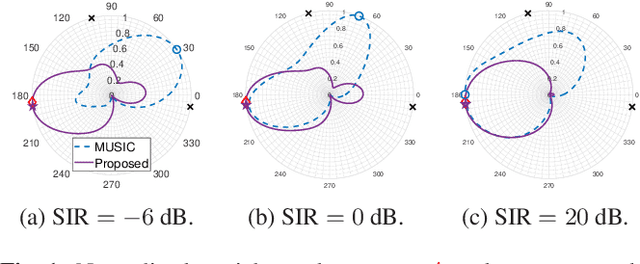
Deep neural networks (DNNs) have greatly benefited direction of arrival (DoA) estimation methods for speech source localization in noisy environments. However, their localization accuracy is still far from satisfactory due to the vulnerability to nonspeech interference. To improve the robustness against interference, we propose a DNN based normalized time-frequency (T-F) weighted criterion which minimizes the distance between the candidate steering vectors and the filtered snapshots in the T-F domain. Our method requires no eigendecomposition and uses a simple normalization to prevent the optimization objective from being misled by noisy filtered snapshots. We also study different designs of T-F weights guided by a DNN. We find that duplicating the Hadamard product of speech ratio masks is highly effective and better than other techniques such as direct masking and taking the mean in the proposed approach. However, the best-performing design of T-F weights is criterion-dependent in general. Experiments show that the proposed method outperforms popular DNN based DoA estimation methods including widely used subspace methods in noisy and reverberant environments.

Leveraging Heteroscedastic Uncertainty in Learning Complex Spectral Mapping for Single-channel Speech Enhancement

Most speech enhancement (SE) models learn a point estimate, and do not make use of uncertainty estimation in the learning process. In this paper, we show that modeling heteroscedastic uncertainty by minimizing a multivariate Gaussian negative log-likelihood (NLL) improves SE performance at no extra cost. During training, our approach augments a model learning complex spectral mapping with a temporary submodel to predict the covariance of the enhancement error at each time-frequency bin. Due to unrestricted heteroscedastic uncertainty, the covariance introduces an undersampling effect, detrimental to SE performance. To mitigate undersampling, our approach inflates the uncertainty lower bound and weights each loss component with their uncertainty, effectively compensating severely undersampled components with more penalties. Our multivariate setting reveals common covariance assumptions such as scalar and diagonal matrices. By weakening these assumptions, we show that the NLL achieves superior performance compared to popular losses including the mean squared error (MSE), mean absolute error (MAE), and scale-invariant signal-to-distortion ratio (SI-SDR).

Improved Bounds on Neural Complexity for Representing Piecewise Linear Functions

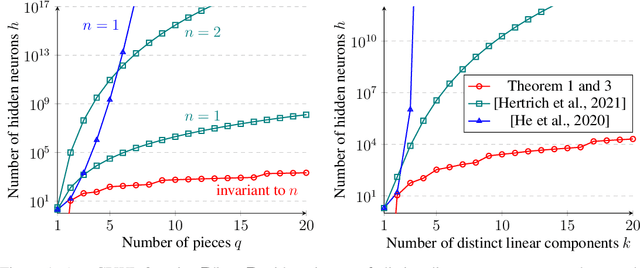
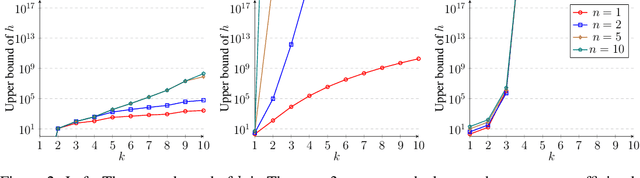
A deep neural network using rectified linear units represents a continuous piecewise linear (CPWL) function and vice versa. Recent results in the literature estimated that the number of neurons needed to exactly represent any CPWL function grows exponentially with the number of pieces or exponentially in terms of the factorial of the number of distinct linear components. Moreover, such growth is amplified linearly with the input dimension. These existing results seem to indicate that the cost of representing a CPWL function is expensive. In this paper, we propose much tighter bounds and establish a polynomial time algorithm to find a network satisfying these bounds for any given CPWL function. We prove that the number of hidden neurons required to exactly represent any CPWL function is at most a quadratic function of the number of pieces. In contrast to all previous results, this upper bound is invariant to the input dimension. Besides the number of pieces, we also study the number of distinct linear components in CPWL functions. When such a number is also given, we prove that the quadratic complexity turns into bilinear, which implies a lower neural complexity because the number of distinct linear components is always not greater than the minimum number of pieces in a CPWL function. When the number of pieces is unknown, we prove that, in terms of the number of distinct linear components, the neural complexity of any CPWL function is at most polynomial growth for low-dimensional inputs and a factorial growth for the worst-case scenario, which are significantly better than existing results in the literature.

A Generalized Proportionate-Type Normalized Subband Adaptive Filter

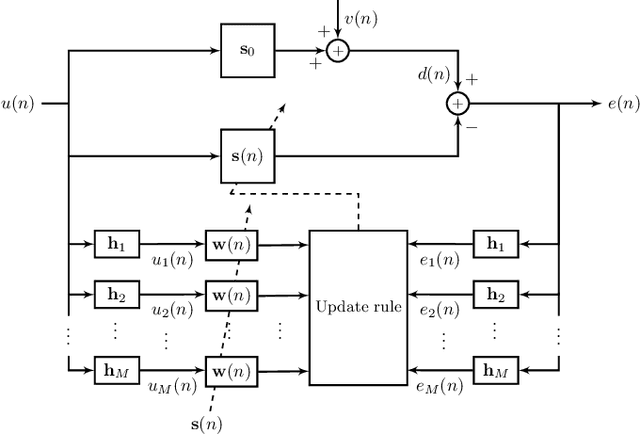
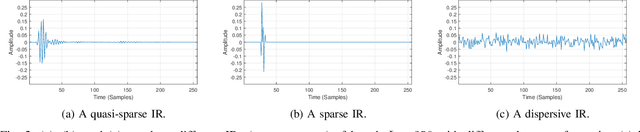
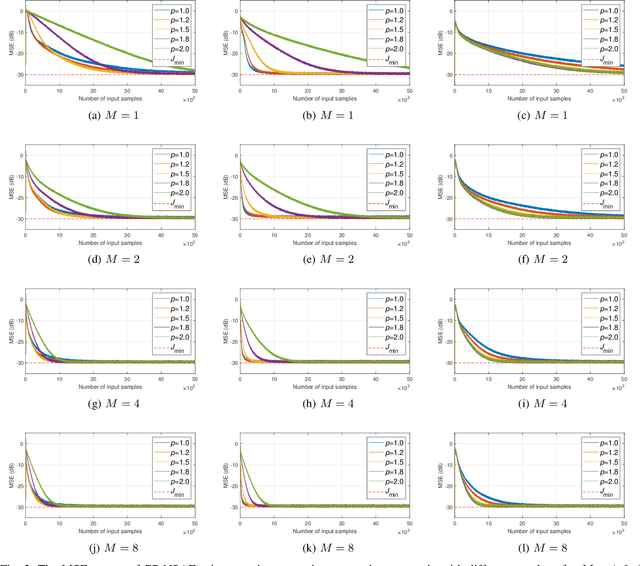
We show that a new design criterion, i.e., the least squares on subband errors regularized by a weighted norm, can be used to generalize the proportionate-type normalized subband adaptive filtering (PtNSAF) framework. The new criterion directly penalizes subband errors and includes a sparsity penalty term which is minimized using the damped regularized Newton's method. The impact of the proposed generalized PtNSAF (GPtNSAF) is studied for the system identification problem via computer simulations. Specifically, we study the effects of using different numbers of subbands and various sparsity penalty terms for quasi-sparse, sparse, and dispersive systems. The results show that the benefit of increasing the number of subbands is larger than promoting sparsity of the estimated filter coefficients when the target system is quasi-sparse or dispersive. On the other hand, for sparse target systems, promoting sparsity becomes more important. More importantly, the two aspects provide complementary and additive benefits to the GPtNSAF for speeding up convergence.

ResNEsts and DenseNEsts: Block-based DNN Models with Improved Representation Guarantees

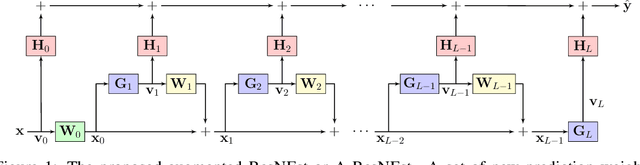
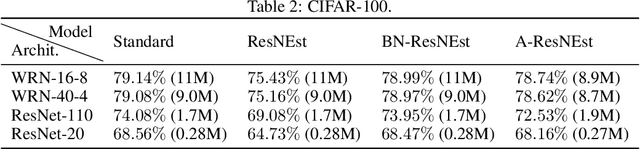
Models recently used in the literature proving residual networks (ResNets) are better than linear predictors are actually different from standard ResNets that have been widely used in computer vision. In addition to the assumptions such as scalar-valued output or single residual block, these models have no nonlinearities at the final residual representation that feeds into the final affine layer. To codify such a difference in nonlinearities and reveal a linear estimation property, we define ResNEsts, i.e., Residual Nonlinear Estimators, by simply dropping nonlinearities at the last residual representation from standard ResNets. We show that wide ResNEsts with bottleneck blocks can always guarantee a very desirable training property that standard ResNets aim to achieve, i.e., adding more blocks does not decrease performance given the same set of basis elements. To prove that, we first recognize ResNEsts are basis function models that are limited by a coupling problem in basis learning and linear prediction. Then, to decouple prediction weights from basis learning, we construct a special architecture termed augmented ResNEst (A-ResNEst) that always guarantees no worse performance with the addition of a block. As a result, such an A-ResNEst establishes empirical risk lower bounds for a ResNEst using corresponding bases. Our results demonstrate ResNEsts indeed have a problem of diminishing feature reuse; however, it can be avoided by sufficiently expanding or widening the input space, leading to the above-mentioned desirable property. Inspired by the DenseNets that have been shown to outperform ResNets, we also propose a corresponding new model called Densely connected Nonlinear Estimator (DenseNEst). We show that any DenseNEst can be represented as a wide ResNEst with bottleneck blocks. Unlike ResNEsts, DenseNEsts exhibit the desirable property without any special architectural re-design.

Deep Learning and Control Algorithms of Direct Perception for Autonomous Driving

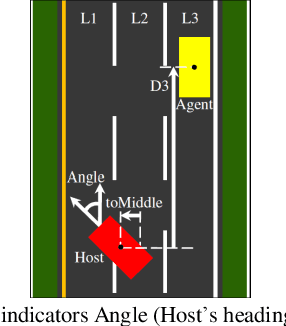
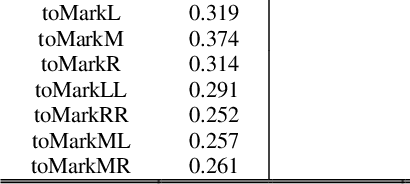
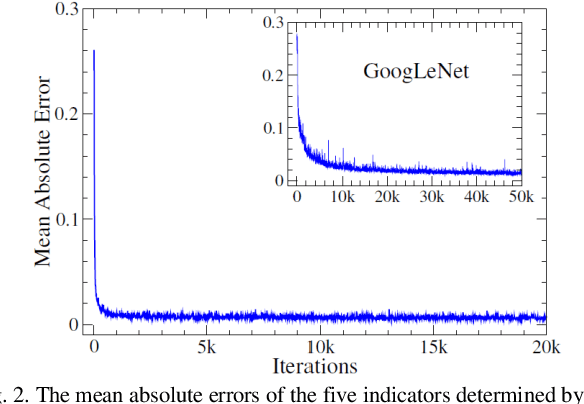
Based on the direct perception paradigm of autonomous driving, we investigate and modify the CNNs (convolutional neural networks) AlexNet and GoogLeNet that map an input image to few perception indicators (heading angle, distances to preceding cars, and distance to road centerline) for estimating driving affordances in highway traffic. We also design a controller with these indicators and the short-range sensor information of TORCS (the open racing car simulator) for driving simulated cars to avoid collisions. We collect a set of images from a TORCS camera in various driving scenarios, train these CNNs using the dataset, test them in unseen traffics, and find that they perform better than earlier algorithms and controllers in terms of training efficiency and driving stability. Source code and data are available on our website.

Team NCTU: Toward AI-Driving for Autonomous Surface Vehicles -- From Duckietown to RobotX

Robotic software and hardware systems of autonomous surface vehicles have been developed in transportation, military, and ocean researches for decades. Previous efforts in RobotX Challenges 2014 and 2016 facilitates the developments for important tasks such as obstacle avoidance and docking. Team NCTU is motivated by the AI Driving Olympics (AI-DO) developed by the Duckietown community, and adopts the principles to RobotX challenge. With the containerization (Docker) and uniformed AI agent (with observations and actions), we could better 1) integrate solutions developed in different middlewares (ROS and MOOS), 2) develop essential functionalities of from simulation (Gazebo) to real robots (either miniaturized or full-sized WAM-V), and 3) compare different approaches either from classic model-based or learning-based. Finally, we setup an outdoor on-surface platform with localization services for evaluation. Some of the preliminary results will be presented for the Team NCTU participations of the RobotX competition in Hawaii in 2018.

Duckiefloat: a Collision-Tolerant Resource-Constrained Blimp for Long-Term Autonomy in Subterranean Environments

There are several challenges for search and rescue robots: mobility, perception, autonomy, and communication. Inspired by the DARPA Subterranean (SubT) Challenge, we propose an autonomous blimp robot, which has the advantages of low power consumption and collision-tolerance compared to other aerial vehicles like drones. This is important for search and rescue tasks that usually last for one or more hours. However, the underground constrained passages limit the size of blimp envelope and its payload, making the proposed system resource-constrained. Therefore, a careful design consideration is needed to build a blimp system with on-board artifact search and SLAM. In order to reach long-term operation, a failure-aware algorithm with minimal communication to human supervisor to have situational awareness and send control signals to the blimp when needed.