Subspace Representation Learning for Sparse Linear Arrays to Localize More Sources than Sensors: A Deep Learning Methodology
Paper and Code
Aug 29, 2024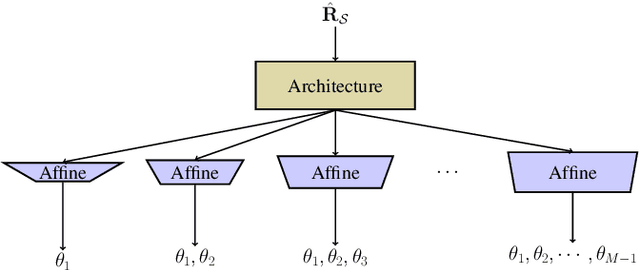
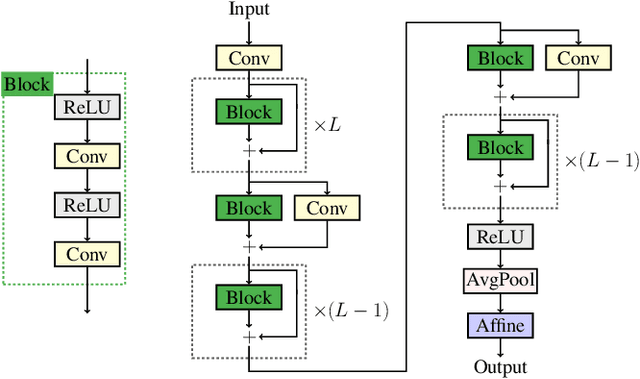
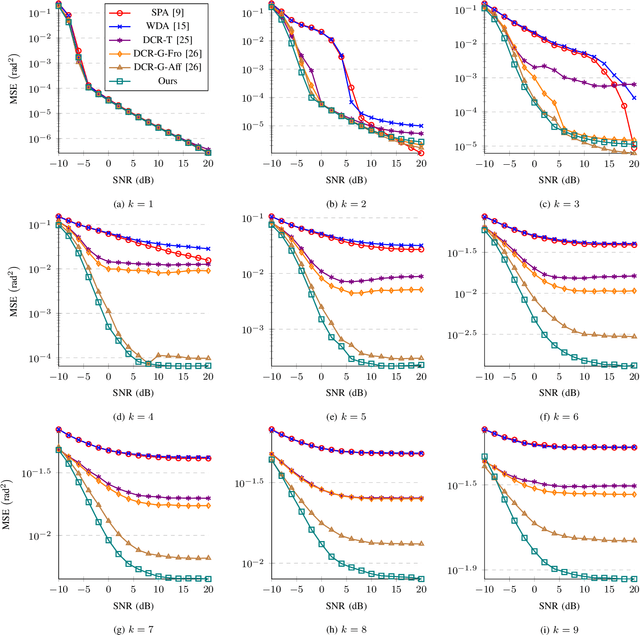
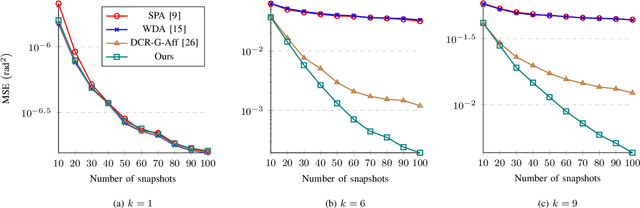
Localizing more sources than sensors with a sparse linear array (SLA) has long relied on minimizing a distance between two covariance matrices and recent algorithms often utilize semidefinite programming (SDP). Although deep neural network (DNN)-based methods offer new alternatives, they still depend on covariance matrix fitting. In this paper, we develop a novel methodology that estimates the co-array subspaces from a sample covariance for SLAs. Our methodology trains a DNN to learn signal and noise subspace representations that are invariant to the selection of bases. To learn such representations, we propose loss functions that gauge the separation between the desired and the estimated subspace. In particular, we propose losses that measure the length of the shortest path between subspaces viewed on a union of Grassmannians, and prove that it is possible for a DNN to approximate signal subspaces. The computation of learning subspaces of different dimensions is accelerated by a new batch sampling strategy called consistent rank sampling. The methodology is robust to array imperfections due to its geometry-agnostic and data-driven nature. In addition, we propose a fully end-to-end gridless approach that directly learns angles to study the possibility of bypassing subspace methods. Numerical results show that learning such subspace representations is more beneficial than learning covariances or angles. It outperforms conventional SDP-based methods such as the sparse and parametric approach (SPA) and existing DNN-based covariance reconstruction methods for a wide range of signal-to-noise ratios (SNRs), snapshots, and source numbers for both perfect and imperfect arrays.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge