A DNN based Normalized Time-frequency Weighted Criterion for Robust Wideband DoA Estimation

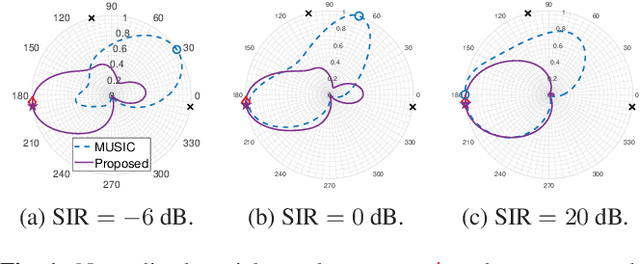
Deep neural networks (DNNs) have greatly benefited direction of arrival (DoA) estimation methods for speech source localization in noisy environments. However, their localization accuracy is still far from satisfactory due to the vulnerability to nonspeech interference. To improve the robustness against interference, we propose a DNN based normalized time-frequency (T-F) weighted criterion which minimizes the distance between the candidate steering vectors and the filtered snapshots in the T-F domain. Our method requires no eigendecomposition and uses a simple normalization to prevent the optimization objective from being misled by noisy filtered snapshots. We also study different designs of T-F weights guided by a DNN. We find that duplicating the Hadamard product of speech ratio masks is highly effective and better than other techniques such as direct masking and taking the mean in the proposed approach. However, the best-performing design of T-F weights is criterion-dependent in general. Experiments show that the proposed method outperforms popular DNN based DoA estimation methods including widely used subspace methods in noisy and reverberant environments.

Improved Bounds on Neural Complexity for Representing Piecewise Linear Functions

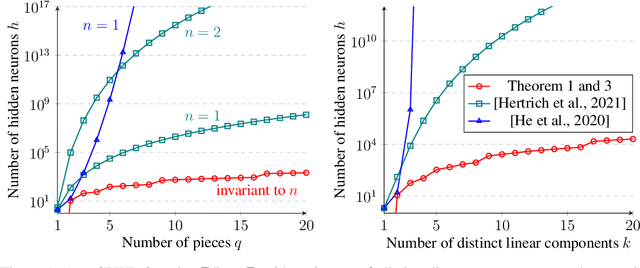
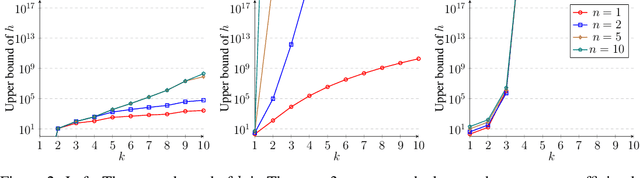
A deep neural network using rectified linear units represents a continuous piecewise linear (CPWL) function and vice versa. Recent results in the literature estimated that the number of neurons needed to exactly represent any CPWL function grows exponentially with the number of pieces or exponentially in terms of the factorial of the number of distinct linear components. Moreover, such growth is amplified linearly with the input dimension. These existing results seem to indicate that the cost of representing a CPWL function is expensive. In this paper, we propose much tighter bounds and establish a polynomial time algorithm to find a network satisfying these bounds for any given CPWL function. We prove that the number of hidden neurons required to exactly represent any CPWL function is at most a quadratic function of the number of pieces. In contrast to all previous results, this upper bound is invariant to the input dimension. Besides the number of pieces, we also study the number of distinct linear components in CPWL functions. When such a number is also given, we prove that the quadratic complexity turns into bilinear, which implies a lower neural complexity because the number of distinct linear components is always not greater than the minimum number of pieces in a CPWL function. When the number of pieces is unknown, we prove that, in terms of the number of distinct linear components, the neural complexity of any CPWL function is at most polynomial growth for low-dimensional inputs and a factorial growth for the worst-case scenario, which are significantly better than existing results in the literature.

A Generalized Proportionate-Type Normalized Subband Adaptive Filter

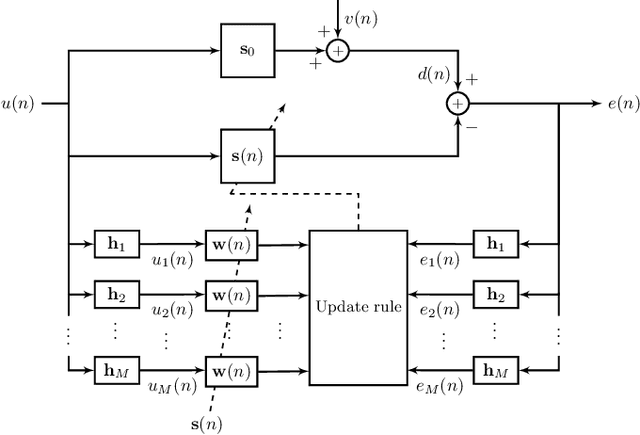
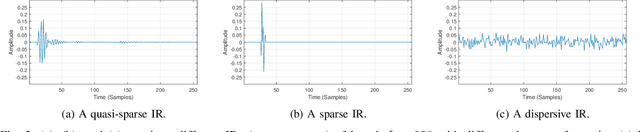
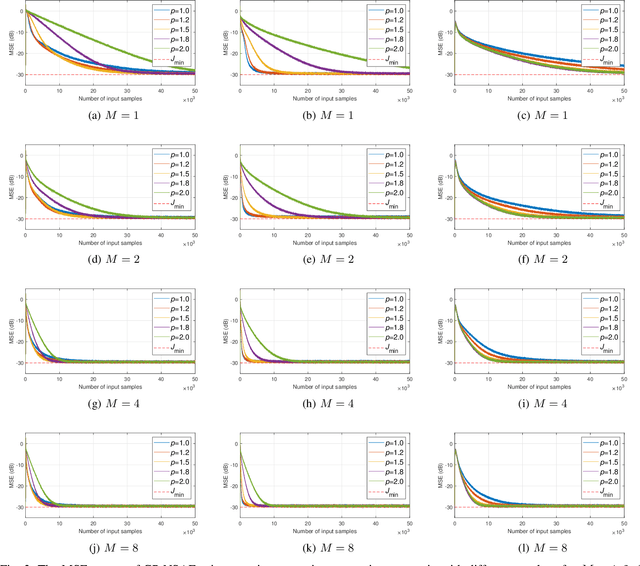
We show that a new design criterion, i.e., the least squares on subband errors regularized by a weighted norm, can be used to generalize the proportionate-type normalized subband adaptive filtering (PtNSAF) framework. The new criterion directly penalizes subband errors and includes a sparsity penalty term which is minimized using the damped regularized Newton's method. The impact of the proposed generalized PtNSAF (GPtNSAF) is studied for the system identification problem via computer simulations. Specifically, we study the effects of using different numbers of subbands and various sparsity penalty terms for quasi-sparse, sparse, and dispersive systems. The results show that the benefit of increasing the number of subbands is larger than promoting sparsity of the estimated filter coefficients when the target system is quasi-sparse or dispersive. On the other hand, for sparse target systems, promoting sparsity becomes more important. More importantly, the two aspects provide complementary and additive benefits to the GPtNSAF for speeding up convergence.

ResNEsts and DenseNEsts: Block-based DNN Models with Improved Representation Guarantees

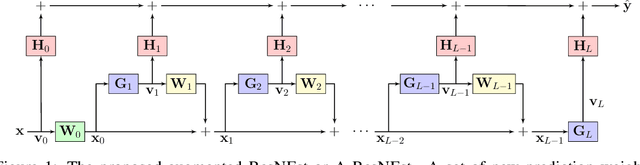
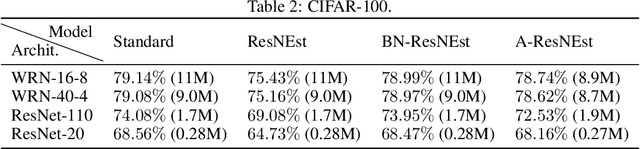
Models recently used in the literature proving residual networks (ResNets) are better than linear predictors are actually different from standard ResNets that have been widely used in computer vision. In addition to the assumptions such as scalar-valued output or single residual block, these models have no nonlinearities at the final residual representation that feeds into the final affine layer. To codify such a difference in nonlinearities and reveal a linear estimation property, we define ResNEsts, i.e., Residual Nonlinear Estimators, by simply dropping nonlinearities at the last residual representation from standard ResNets. We show that wide ResNEsts with bottleneck blocks can always guarantee a very desirable training property that standard ResNets aim to achieve, i.e., adding more blocks does not decrease performance given the same set of basis elements. To prove that, we first recognize ResNEsts are basis function models that are limited by a coupling problem in basis learning and linear prediction. Then, to decouple prediction weights from basis learning, we construct a special architecture termed augmented ResNEst (A-ResNEst) that always guarantees no worse performance with the addition of a block. As a result, such an A-ResNEst establishes empirical risk lower bounds for a ResNEst using corresponding bases. Our results demonstrate ResNEsts indeed have a problem of diminishing feature reuse; however, it can be avoided by sufficiently expanding or widening the input space, leading to the above-mentioned desirable property. Inspired by the DenseNets that have been shown to outperform ResNets, we also propose a corresponding new model called Densely connected Nonlinear Estimator (DenseNEst). We show that any DenseNEst can be represented as a wide ResNEst with bottleneck blocks. Unlike ResNEsts, DenseNEsts exhibit the desirable property without any special architectural re-design.

Intermittent Speech Recovery

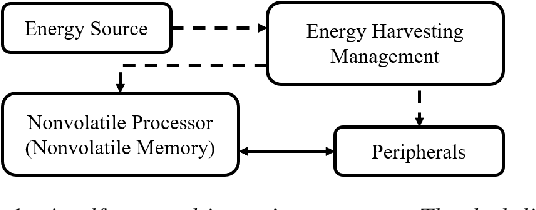
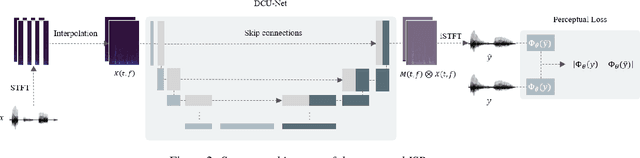
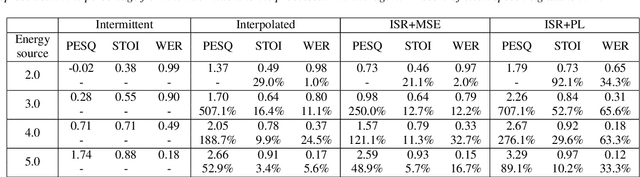
A large number of Internet of Things (IoT) devices today are powered by batteries, which are often expensive to maintain and may cause serious environmental pollution. To avoid these problems, researchers have begun to consider the use of energy systems based on energy-harvesting units for such devices. However, the power harvested from an ambient source is fundamentally small and unstable, resulting in frequent power failures during the operation of IoT applications involving, for example, intermittent speech signals and the streaming of videos. This paper presents a deep-learning-based speech recovery system that reconstructs intermittent speech signals from self-powered IoT devices. Our intermittent speech recovery system (ISR) consists of three stages: interpolation, recovery, and combination. The experimental results show that our recovery system increases speech quality by up to 707.1%, while increasing speech intelligibility by up to 92.1%. Most importantly, our ISR system also enhances the WER scores by up to 65.6%. To the best of our knowledge, this study is one of the first to reconstruct intermittent speech signals from self-powered-sensing IoT devices. These promising results suggest that even though self powered microphone devices function with weak energy sources, our ISR system can still maintain the performance of most speech-signal-based applications.

A Unified Framework for Sparse Non-Negative Least Squares using Multiplicative Updates and the Non-Negative Matrix Factorization Problem

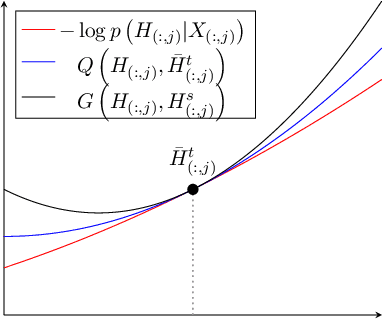
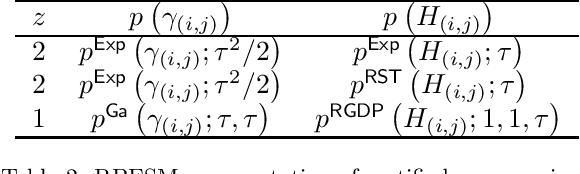
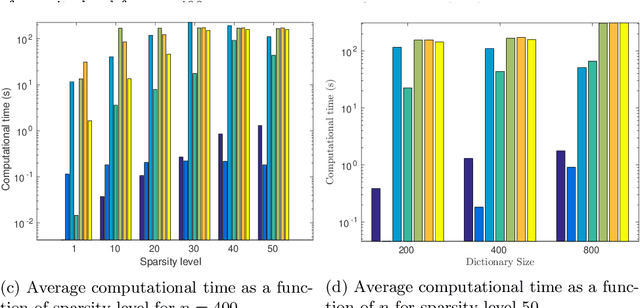
We study the sparse non-negative least squares (S-NNLS) problem. S-NNLS occurs naturally in a wide variety of applications where an unknown, non-negative quantity must be recovered from linear measurements. We present a unified framework for S-NNLS based on a rectified power exponential scale mixture prior on the sparse codes. We show that the proposed framework encompasses a large class of S-NNLS algorithms and provide a computationally efficient inference procedure based on multiplicative update rules. Such update rules are convenient for solving large sets of S-NNLS problems simultaneously, which is required in contexts like sparse non-negative matrix factorization (S-NMF). We provide theoretical justification for the proposed approach by showing that the local minima of the objective function being optimized are sparse and the S-NNLS algorithms presented are guaranteed to converge to a set of stationary points of the objective function. We then extend our framework to S-NMF, showing that our framework leads to many well known S-NMF algorithms under specific choices of prior and providing a guarantee that a popular subclass of the proposed algorithms converges to a set of stationary points of the objective function. Finally, we study the performance of the proposed approaches on synthetic and real-world data.