Machine Learning Applications Related to Suicide in Military and Veterans: A Scoping Literature Review

Suicide remains one of the main preventable causes of death among active service members and veterans. Early detection and prediction are crucial in suicide prevention. Machine learning techniques have yielded promising results in this area recently. This study aims to assess and summarize current research and provides a comprehensive review regarding the application of machine learning techniques in assessing and predicting suicidal ideation, attempts, and mortality among members of military and veteran populations. A keyword search using PubMed, IEEE, ACM, and Google Scholar was conducted, and the PRISMA protocol was adopted for relevant study selection. Thirty-two articles met the inclusion criteria. These studies consistently identified risk factors relevant to mental health issues such as depression, post-traumatic stress disorder (PTSD), suicidal ideation, prior attempts, physical health problems, and demographic characteristics. Machine learning models applied in this area have demonstrated reasonable predictive accuracy. However, additional research gaps still exist. First, many studies have overlooked metrics that distinguish between false positives and negatives, such as positive predictive value and negative predictive value, which are crucial in the context of suicide prevention policies. Second, more dedicated approaches to handling survival and longitudinal data should be explored. Lastly, most studies focused on machine learning methods, with limited discussion of their connection to clinical rationales. In summary, machine learning analyses have identified a wide range of risk factors associated with suicide in military populations. The diversity and complexity of these factors also demonstrates that effective prevention strategies must be comprehensive and flexible.

Deciphering genomic codes using advanced NLP techniques: a scoping review

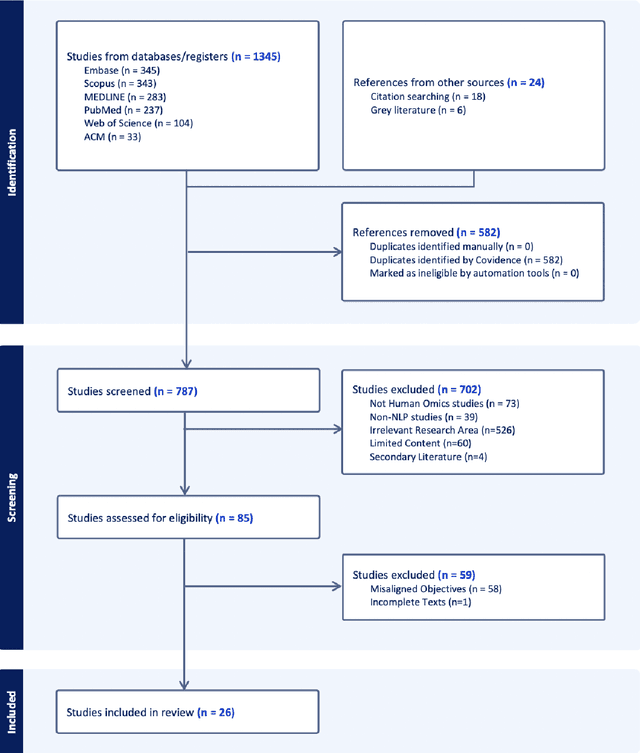
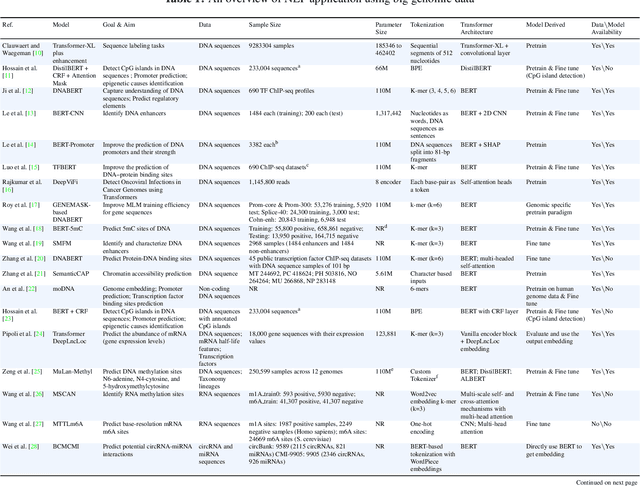
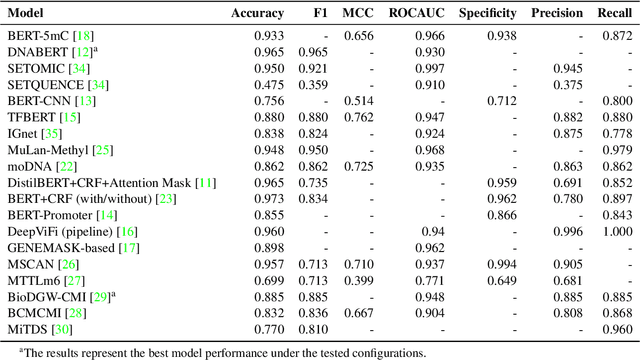
Objectives: The vast and complex nature of human genomic sequencing data presents challenges for effective analysis. This review aims to investigate the application of Natural Language Processing (NLP) techniques, particularly Large Language Models (LLMs) and transformer architectures, in deciphering genomic codes, focusing on tokenization, transformer models, and regulatory annotation prediction. The goal of this review is to assess data and model accessibility in the most recent literature, gaining a better understanding of the existing capabilities and constraints of these tools in processing genomic sequencing data. Methods: Following Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines, our scoping review was conducted across PubMed, Medline, Scopus, Web of Science, Embase, and ACM Digital Library. Studies were included if they focused on NLP methodologies applied to genomic sequencing data analysis, without restrictions on publication date or article type. Results: A total of 26 studies published between 2021 and April 2024 were selected for review. The review highlights that tokenization and transformer models enhance the processing and understanding of genomic data, with applications in predicting regulatory annotations like transcription-factor binding sites and chromatin accessibility. Discussion: The application of NLP and LLMs to genomic sequencing data interpretation is a promising field that can help streamline the processing of large-scale genomic data while also providing a better understanding of its complex structures. It has the potential to drive advancements in personalized medicine by offering more efficient and scalable solutions for genomic analysis. Further research is also needed to discuss and overcome current limitations, enhancing model transparency and applicability.

Realtime Safety Control for Bipedal Robots to Avoid Multiple Obstacles via CLF-CBF Constraints

This paper presents a reactive planning system that allows a Cassie-series bipedal robot to avoid multiple non-overlapping obstacles via a single, continuously differentiable control barrier function (CBF). The overall system detects an individual obstacle via a height map derived from a LiDAR point cloud and computes an elliptical outer approximation, which is then turned into a CBF. The QP-CLF-CBF formalism developed by Ames et al. is applied to ensure that safe trajectories are generated. Liveness is ensured by an analysis of induced equilibrium points that are distinct from the goal state. Safe planning in environments with multiple obstacles is demonstrated both in simulation and experimentally on the Cassie biped.

Bayes estimators for phylogenetic reconstruction

Tree reconstruction methods are often judged by their accuracy, measured by how close they get to the true tree. Yet most reconstruction methods like ML do not explicitly maximize this accuracy. To address this problem, we propose a Bayesian solution. Given tree samples, we propose finding the tree estimate which is closest on average to the samples. This ``median'' tree is known as the Bayes estimator (BE). The BE literally maximizes posterior expected accuracy, measured in terms of closeness (distance) to the true tree. We discuss a unified framework of BE trees, focusing especially on tree distances which are expressible as squared euclidean distances. Notable examples include Robinson--Foulds distance, quartet distance, and squared path difference. Using simulated data, we show Bayes estimators can be efficiently computed in practice by hill climbing. We also show that Bayes estimators achieve higher accuracy, compared to maximum likelihood and neighbor joining.