Phase Object Reconstruction for 4D-STEM using Deep Learning

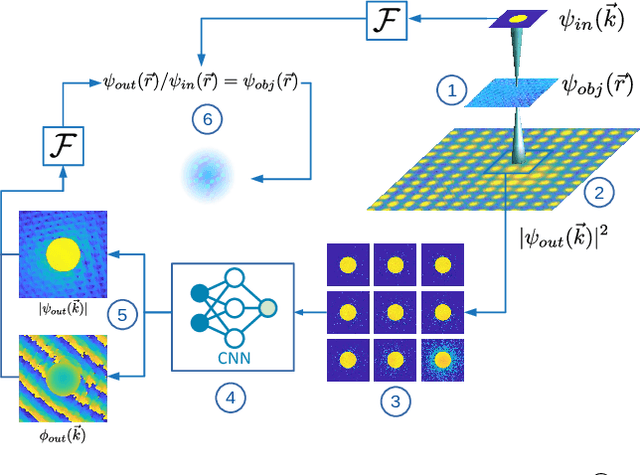
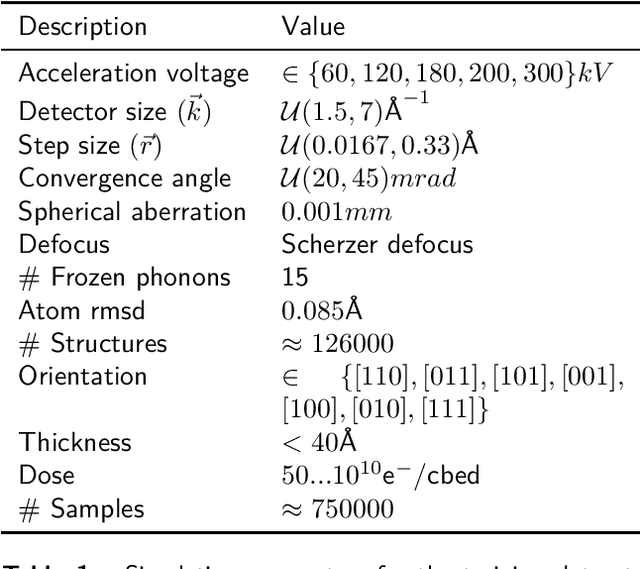
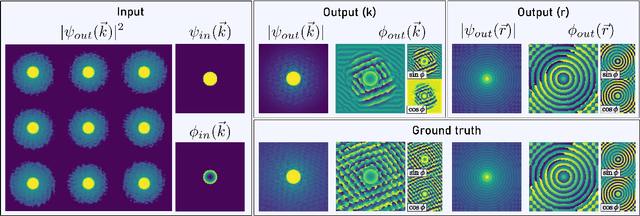
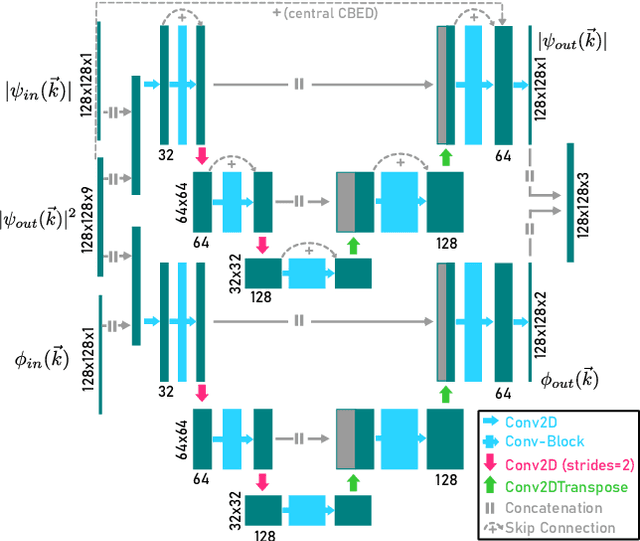
In this study we explore the possibility to use deep learning for the reconstruction of phase images from 4D scanning transmission electron microscopy (4D-STEM) data. The process can be divided into two main steps. First, the complex electron wave function is recovered for a convergent beam electron diffraction pattern (CBED) using a convolutional neural network (CNN). Subsequently a corresponding patch of the phase object is recovered using the phase object approximation (POA). Repeating this for each scan position in a 4D-STEM dataset and combining the patches by complex summation yields the full phase object. Each patch is recovered from a kernel of 3x3 adjacent CBEDs only, which eliminates common, large memory requirements and enables live processing during an experiment. The machine learning pipeline, data generation and the reconstruction algorithm are presented. We demonstrate that the CNN can retrieve phase information beyond the aperture angle, enabling super-resolution imaging. The image contrast formation is evaluated showing a dependence on thickness and atomic column type. Columns containing light and heavy elements can be imaged simultaneously and are distinguishable. The combination of super-resolution, good noise robustness and intuitive image contrast characteristics makes the approach unique among live imaging methods in 4D-STEM.

Real Time Integration Centre of Mass (riCOM) Reconstruction for 4D-STEM

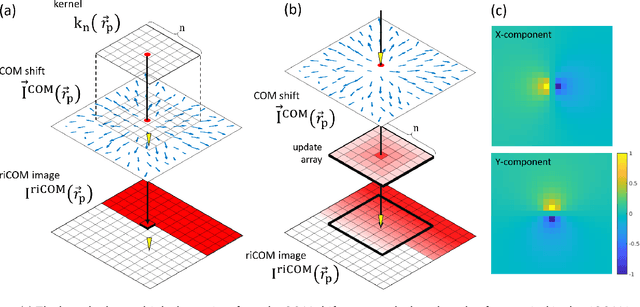
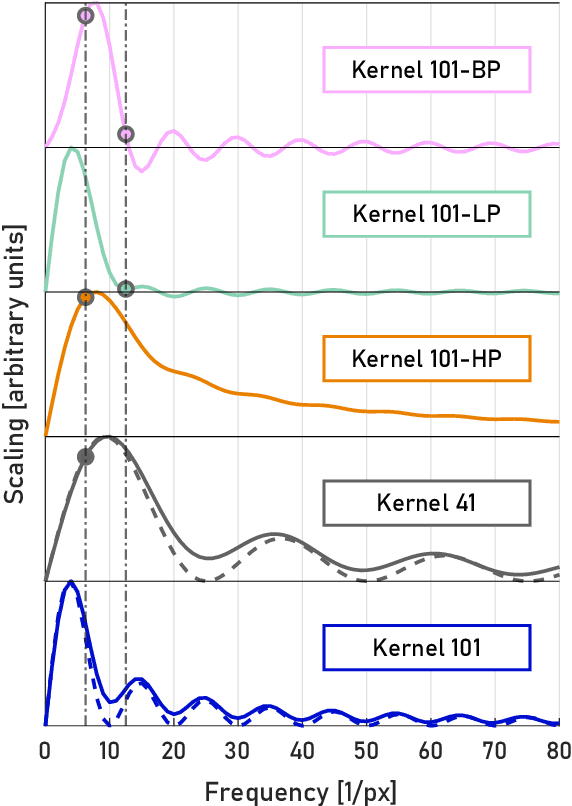
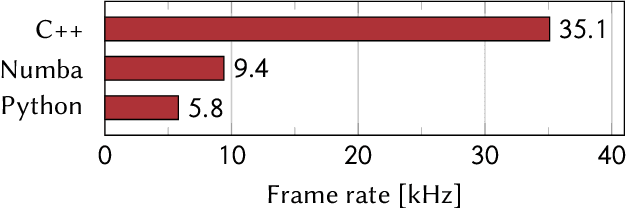
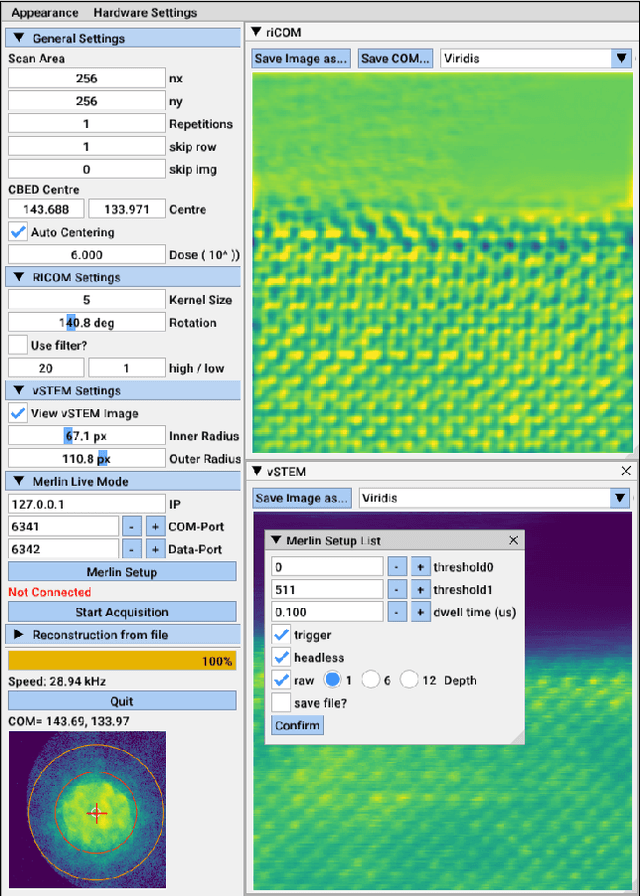
A real-time image reconstruction method for scanning transmission electron microscopy (STEM) is proposed. With an algorithm requiring only the center of mass (COM) of the diffraction pattern at one probe position at a time, it is able to update the resulting image each time a new probe position is visited without storing any intermediate diffraction patterns. The results show clear features at higher spatial frequency, such as atomic column positions. It is also demonstrated that some common post processing methods, such as band pass filtering, can be directly integrated in the real time processing flow. Compared with other reconstruction methods, the proposed method produces high quality reconstructions with good noise robustness at extremely low memory and computational requirements. An efficient, interactive open source implementation of the concept is further presented, which is compatible with frame-based, as well as event-based camera/file types. This method provides the attractive feature of immediate feedback that microscope operators have become used to, e.g. conventional high angle annular dark field STEM imaging, allowing for rapid decision making and fine tuning to obtain the best possible images for beam sensitive samples at the lowest possible dose.

Phase retrieval from 4-dimensional electron diffraction datasets

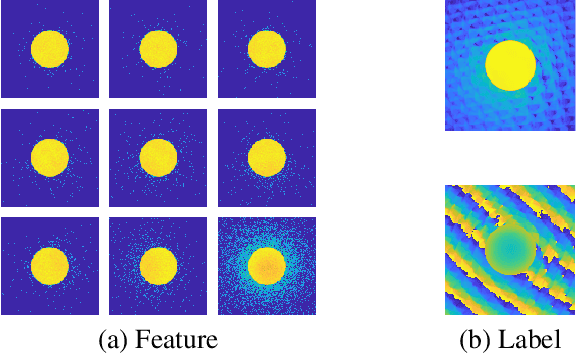
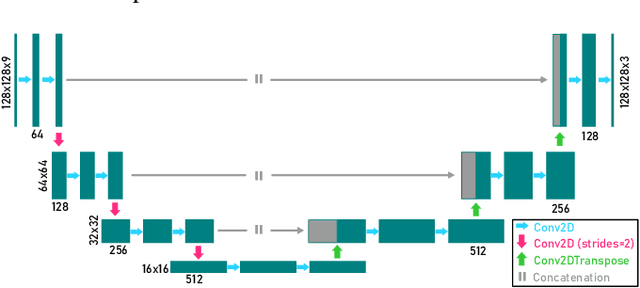
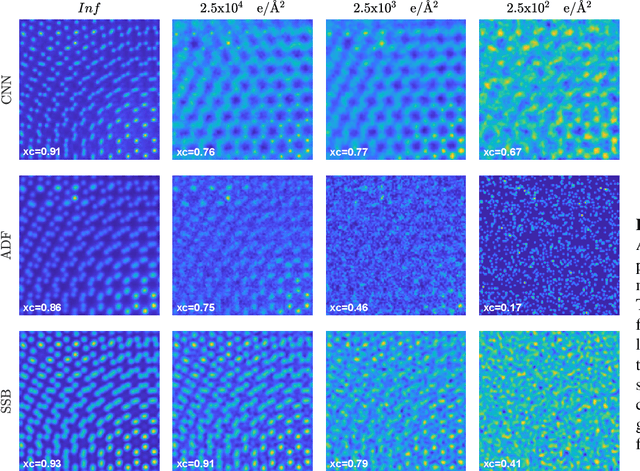
We present a computational imaging mode for large scale electron microscopy data, which retrieves a complex wave from noisy/sparse intensity recordings using a deep learning approach and subsequently reconstructs an image of the specimen from the Convolutional Neural Network (CNN) predicted exit waves. We demonstrate that an appropriate forward model in combination with open data frameworks can be used to generate large synthetic datasets for training. In combination with augmenting the data with Poisson noise corresponding to varying dose-values, we effectively eliminate overfitting issues. The U-NET based architecture of the CNN is adapted to the task at hand and performs well while maintaining a relatively small size and fast performance. The validity of the approach is confirmed by comparing the reconstruction to well-established methods using simulated, as well as real electron microscopy data. The proposed method is shown to be effective particularly in the low dose range, evident by strong suppression of noise, good spatial resolution, and sensitivity to different atom types, enabling the simultaneous visualisation of light and heavy elements and making different atomic species distinguishable. Since the method acts on a very local scale and is comparatively fast it bears the potential to be used for near-real-time reconstruction during data acquisition.

Bayes estimators for phylogenetic reconstruction

Tree reconstruction methods are often judged by their accuracy, measured by how close they get to the true tree. Yet most reconstruction methods like ML do not explicitly maximize this accuracy. To address this problem, we propose a Bayesian solution. Given tree samples, we propose finding the tree estimate which is closest on average to the samples. This ``median'' tree is known as the Bayes estimator (BE). The BE literally maximizes posterior expected accuracy, measured in terms of closeness (distance) to the true tree. We discuss a unified framework of BE trees, focusing especially on tree distances which are expressible as squared euclidean distances. Notable examples include Robinson--Foulds distance, quartet distance, and squared path difference. Using simulated data, we show Bayes estimators can be efficiently computed in practice by hill climbing. We also show that Bayes estimators achieve higher accuracy, compared to maximum likelihood and neighbor joining.