Canonical Autocorrelation Analysis

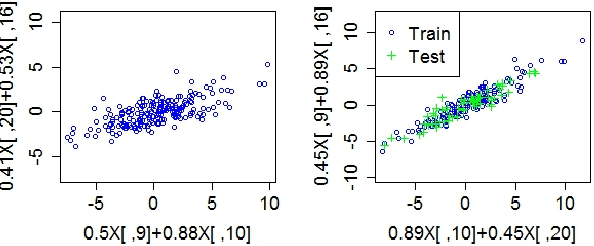
We present an extension of sparse Canonical Correlation Analysis (CCA) designed for finding multiple-to-multiple linear correlations within a single set of variables. Unlike CCA, which finds correlations between two sets of data where the rows are matched exactly but the columns represent separate sets of variables, the method proposed here, Canonical Autocorrelation Analysis (CAA), finds multivariate correlations within just one set of variables. This can be useful when we look for hidden parsimonious structures in data, each involving only a small subset of all features. In addition, the discovered correlations are highly interpretable as they are formed by pairs of sparse linear combinations of the original features. We show how CAA can be of use as a tool for anomaly detection when the expected structure of correlations is not followed by anomalous data. We illustrate the utility of CAA in two application domains where single-class and unsupervised learning of correlation structures are particularly relevant: breast cancer diagnosis and radiation threat detection. When applied to the Wisconsin Breast Cancer data, single-class CAA is competitive with supervised methods used in literature. On the radiation threat detection task, unsupervised CAA performs significantly better than an unsupervised alternative prevalent in the domain, while providing valuable additional insights for threat analysis.

Bayes estimators for phylogenetic reconstruction

Tree reconstruction methods are often judged by their accuracy, measured by how close they get to the true tree. Yet most reconstruction methods like ML do not explicitly maximize this accuracy. To address this problem, we propose a Bayesian solution. Given tree samples, we propose finding the tree estimate which is closest on average to the samples. This ``median'' tree is known as the Bayes estimator (BE). The BE literally maximizes posterior expected accuracy, measured in terms of closeness (distance) to the true tree. We discuss a unified framework of BE trees, focusing especially on tree distances which are expressible as squared euclidean distances. Notable examples include Robinson--Foulds distance, quartet distance, and squared path difference. Using simulated data, we show Bayes estimators can be efficiently computed in practice by hill climbing. We also show that Bayes estimators achieve higher accuracy, compared to maximum likelihood and neighbor joining.