Tropical Attention: Neural Algorithmic Reasoning for Combinatorial Algorithms

Dynamic programming (DP) algorithms for combinatorial optimization problems work with taking maximization, minimization, and classical addition in their recursion algorithms. The associated value functions correspond to convex polyhedra in the max plus semiring. Existing Neural Algorithmic Reasoning models, however, rely on softmax-normalized dot-product attention where the smooth exponential weighting blurs these sharp polyhedral structures and collapses when evaluated on out-of-distribution (OOD) settings. We introduce Tropical attention, a novel attention function that operates natively in the max-plus semiring of tropical geometry. We prove that Tropical attention can approximate tropical circuits of DP-type combinatorial algorithms. We then propose that using Tropical transformers enhances empirical OOD performance in both length generalization and value generalization, on algorithmic reasoning tasks, surpassing softmax baselines while remaining stable under adversarial attacks. We also present adversarial-attack generalization as a third axis for Neural Algorithmic Reasoning benchmarking. Our results demonstrate that Tropical attention restores the sharp, scale-invariant reasoning absent from softmax.

Inference for max-linear Bayesian networks with noise

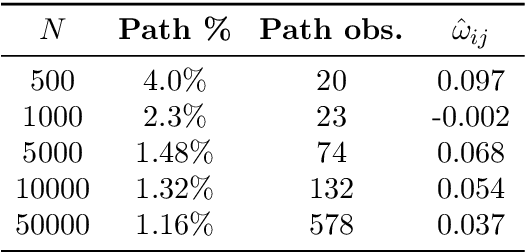
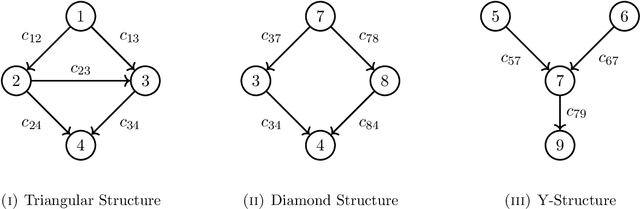
Max-Linear Bayesian Networks (MLBNs) provide a powerful framework for causal inference in extreme-value settings; we consider MLBNs with noise parameters with a given topology in terms of the max-plus algebra by taking its logarithm. Then, we show that an estimator of a parameter for each edge in a directed acyclic graph (DAG) is distributed normally. We end this paper with computational experiments with the expectation and maximization (EM) algorithm and quadratic optimization.

Tropical Bisectors and Carlini-Wagner Attacks

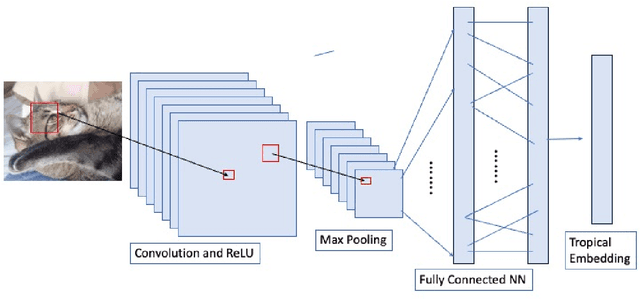
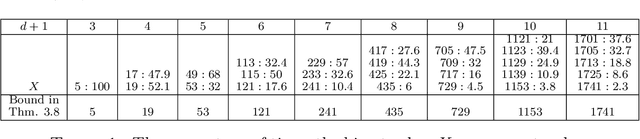
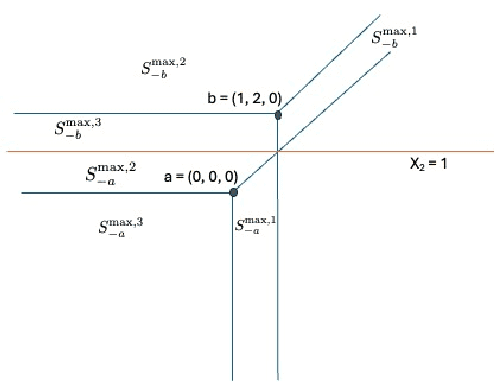
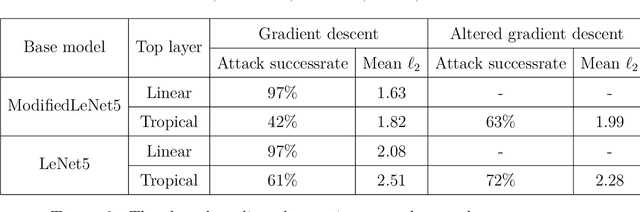
Pasque et al. showed that using a tropical symmetric metric as an activation function in the last layer can improve the robustness of convolutional neural networks (CNNs) against state-of-the-art attacks, including the Carlini-Wagner attack. This improvement occurs when the attacks are not specifically adapted to the non-differentiability of the tropical layer. Moreover, they showed that the decision boundary of a tropical CNN is defined by tropical bisectors. In this paper, we explore the combinatorics of tropical bisectors and analyze how the tropical embedding layer enhances robustness against Carlini-Wagner attacks. We prove an upper bound on the number of linear segments the decision boundary of a tropical CNN can have. We then propose a refined version of the Carlini-Wagner attack, specifically tailored for the tropical architecture. Computational experiments with MNIST and LeNet5 showcase our attacks improved success rate.

Tropical Decision Boundaries for Neural Networks Are Robust Against Adversarial Attacks

We introduce a simple, easy to implement, and computationally efficient tropical convolutional neural network architecture that is robust against adversarial attacks. We exploit the tropical nature of piece-wise linear neural networks by embedding the data in the tropical projective torus in a single hidden layer which can be added to any model. We study the geometry of its decision boundary theoretically and show its robustness against adversarial attacks on image datasets using computational experiments.

Tropical Geometric Tools for Machine Learning: the TML package

In the last decade, developments in tropical geometry have provided a number of uses directly applicable to problems in statistical learning. The TML package is the first R package which contains a comprehensive set of tools and methods used for basic computations related to tropical convexity, visualization of tropically convex sets, as well as supervised and unsupervised learning models using the tropical metric under the max-plus algebra over the tropical projective torus. Primarily, the TML package employs a Hit and Run Markov chain Monte Carlo sampler in conjunction with the tropical metric as its main tool for statistical inference. In addition to basic computation and various applications of the tropical HAR sampler, we also focus on several supervised and unsupervised methods incorporated in the TML package including tropical principal component analysis, tropical logistic regression and tropical kernel density estimation.

Solving reward-collecting problems with UAVs: a comparison of online optimization and Q-learning

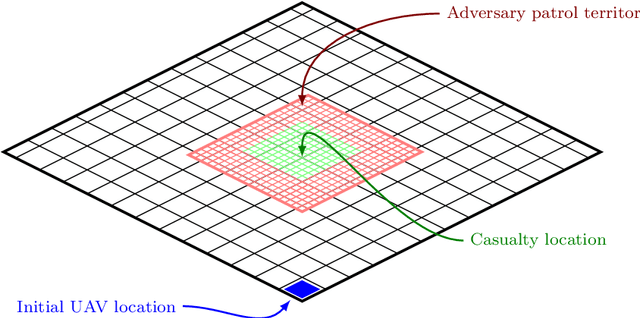
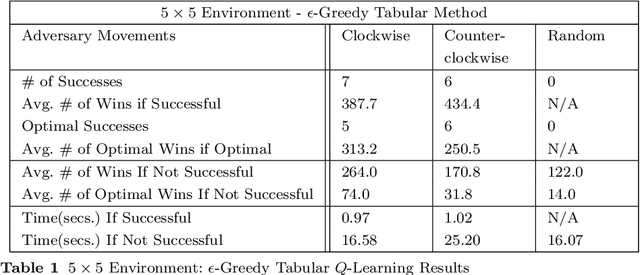
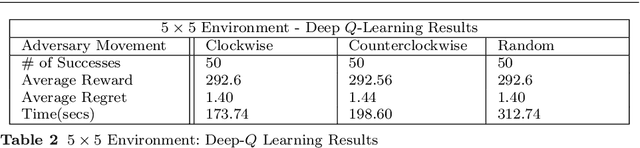
Uncrewed autonomous vehicles (UAVs) have made significant contributions to reconnaissance and surveillance missions in past US military campaigns. As the prevalence of UAVs increases, there has also been improvements in counter-UAV technology that makes it difficult for them to successfully obtain valuable intelligence within an area of interest. Hence, it has become important that modern UAVs can accomplish their missions while maximizing their chances of survival. In this work, we specifically study the problem of identifying a short path from a designated start to a goal, while collecting all rewards and avoiding adversaries that move randomly on the grid. We also provide a possible application of the framework in a military setting, that of autonomous casualty evacuation. We present a comparison of three methods to solve this problem: namely we implement a Deep Q-Learning model, an $\varepsilon$-greedy tabular Q-Learning model, and an online optimization framework. Our computational experiments, designed using simple grid-world environments with random adversaries showcase how these approaches work and compare them in terms of performance, accuracy, and computational time.

SARS-CoV-2 Dissemination using a Network of the United States Counties

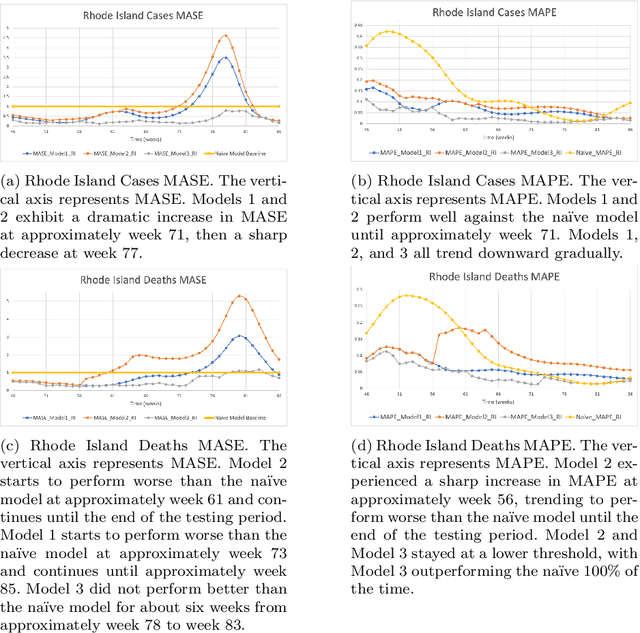
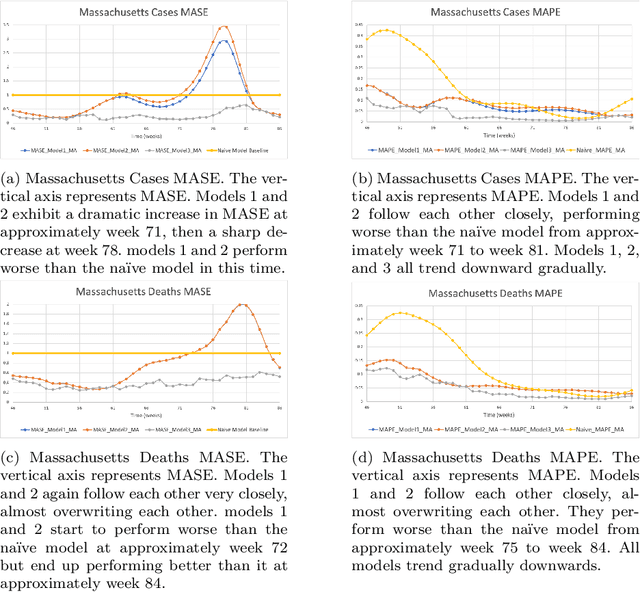
During 2020 and 2021, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) transmission has been increasing amongst the world's population at an alarming rate. Reducing the spread of SARS-CoV-2 and other diseases that are spread in similar manners is paramount for public health officials as they seek to effectively manage resources and potential population control measures such as social distancing and quarantines. By analyzing the United States' county network structure, one can model and interdict potential higher infection areas. County officials can provide targeted information, preparedness training, as well as increase testing in these areas. While these approaches may provide adequate countermeasures for localized areas, they are inadequate for the holistic United States. We solve this problem by collecting coronavirus disease 2019 (COVID-19) infections and deaths from the Center for Disease Control and Prevention and a network adjacency structure from the United States Census Bureau. Generalized network autoregressive (GNAR) time series models have been proposed as an efficient learning algorithm for networked datasets. This work fuses network science and operations research techniques to univariately model COVID-19 cases, deaths, and current survivors across the United States' county network structure.

Tropical Support Vector Machines: Evaluations and Extension to Function Spaces

Support Vector Machines (SVMs) are one of the most popular supervised learning models to classify using a hyperplane in an Euclidean space. Similar to SVMs, tropical SVMs classify data points using a tropical hyperplane under the tropical metric with the max-plus algebra. In this paper, first we show generalization error bounds of tropical SVMs over the tropical projective space. While the generalization error bounds attained via VC dimensions in a distribution-free manner still depend on the dimension, we also show theoretically by extreme value statistics that the tropical SVMs for classifying data points from two Gaussian distributions as well as empirical data sets of different neuron types are fairly robust against the curse of dimensionality. Extreme value statistics also underlie the anomalous scaling behaviors of the tropical distance between random vectors with additional noise dimensions. Finally, we define tropical SVMs over a function space with the tropical metric and discuss the Gaussian function space as an example.

Tropical Data Science

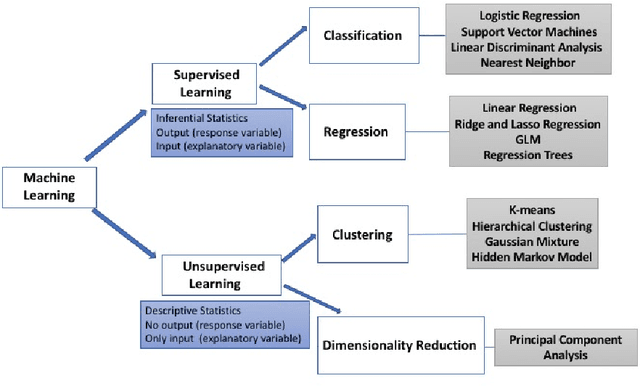
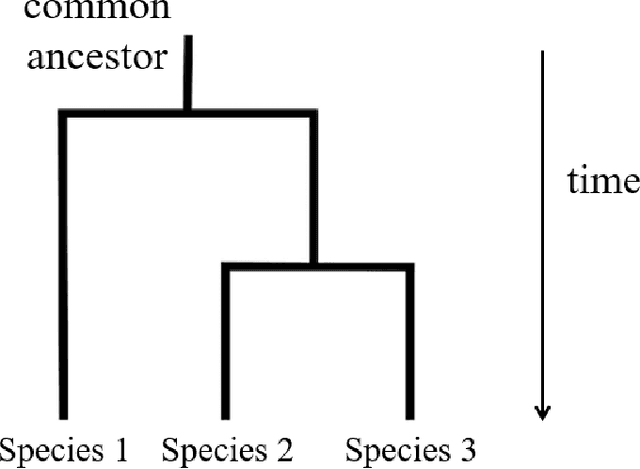
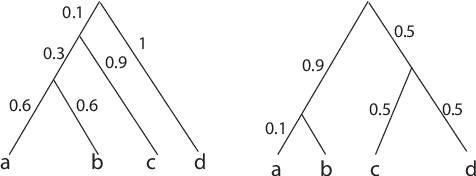
Phylogenomics is a new field which applies to tools in phylogenetics to genome data. Due to a new technology and increasing amount of data, we face new challenges to analyze them over a space of phylogenetic trees. Because a space of phylogenetic trees with a fixed set of labels on leaves is not Euclidean, we cannot simply apply tools in data science. In this paper we survey some new developments of machine learning models using tropical geometry to analyze a set of phylogenetic trees over a tree space.

Tropical Support Vector Machine and its Applications to Phylogenomics

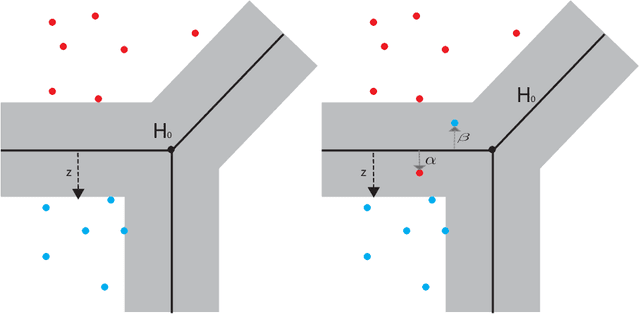
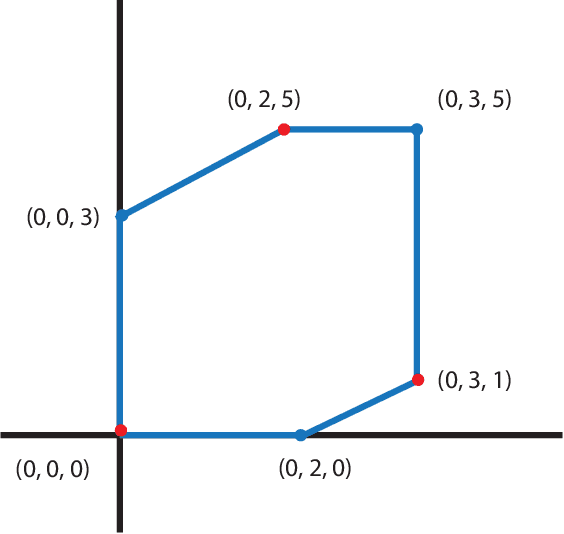
Most data in genome-wide phylogenetic analysis (phylogenomics) is essentially multidimensional, posing a major challenge to human comprehension and computational analysis. Also, we can not directly apply statistical learning models in data science to a set of phylogenetic trees since the space of phylogenetic trees is not Euclidean. In fact, the space of phylogenetic trees is a tropical Grassmannian in terms of max-plus algebra. Therefore, to classify multi-locus data sets for phylogenetic analysis, we propose tropical support vector machines (SVMs). Like classical SVMs, a tropical SVM is a discriminative classifier defined by the tropical hyperplane which maximizes the minimum tropical distance from data points to itself in order to separate these data points into sectors (half-spaces) in the tropical projective torus. Both hard margin tropical SVMs and soft margin tropical SVMs can be formulated as linear programming problems. We focus on classifying two categories of data, and we study a simpler case by assuming the data points from the same category ideally stay in the same sector of a tropical separating hyperplane. For hard margin tropical SVMs, we prove the necessary and sufficient conditions for two categories of data points to be separated, and we show an explicit formula for the optimal value of the feasible linear programming problem. For soft margin tropical SVMs, we develop novel methods to compute an optimal tropical separating hyperplane. Computational experiments show our methods work well. We end this paper with open problems.