Tropical Bisectors and Carlini-Wagner Attacks
Paper and Code
Mar 28, 2025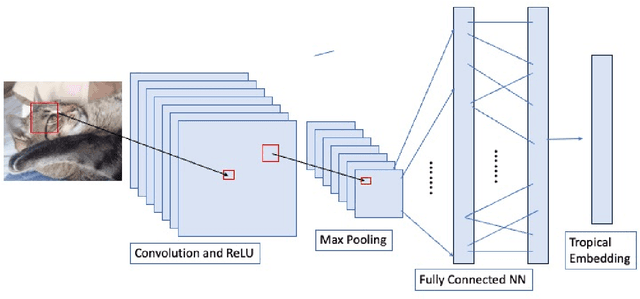
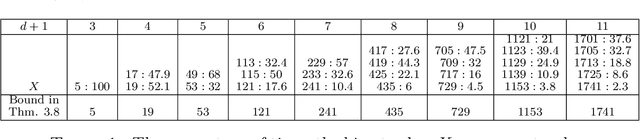
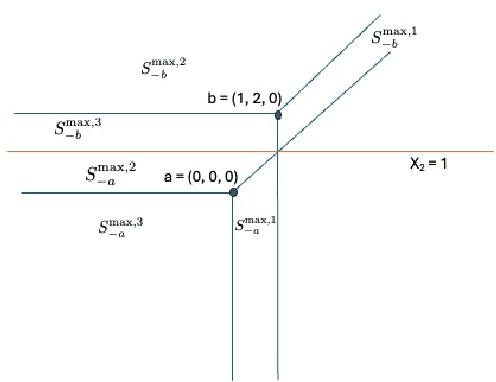
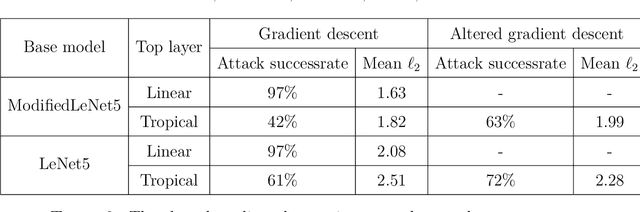
Pasque et al. showed that using a tropical symmetric metric as an activation function in the last layer can improve the robustness of convolutional neural networks (CNNs) against state-of-the-art attacks, including the Carlini-Wagner attack. This improvement occurs when the attacks are not specifically adapted to the non-differentiability of the tropical layer. Moreover, they showed that the decision boundary of a tropical CNN is defined by tropical bisectors. In this paper, we explore the combinatorics of tropical bisectors and analyze how the tropical embedding layer enhances robustness against Carlini-Wagner attacks. We prove an upper bound on the number of linear segments the decision boundary of a tropical CNN can have. We then propose a refined version of the Carlini-Wagner attack, specifically tailored for the tropical architecture. Computational experiments with MNIST and LeNet5 showcase our attacks improved success rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge