Tropical Support Vector Machine and its Applications to Phylogenomics
Paper and Code
Mar 24, 2020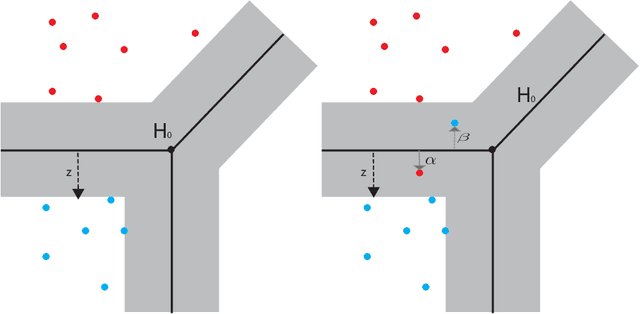

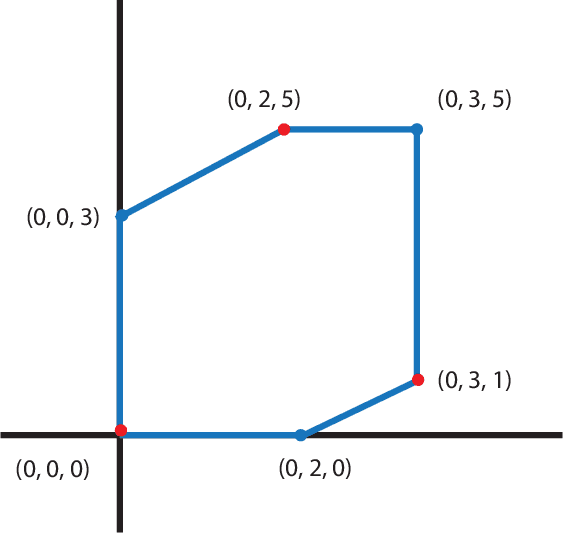
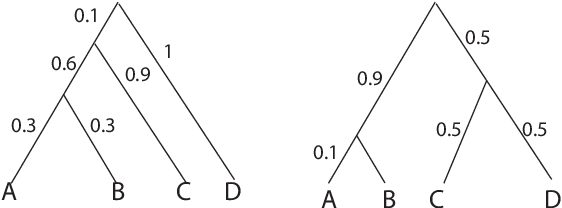
Most data in genome-wide phylogenetic analysis (phylogenomics) is essentially multidimensional, posing a major challenge to human comprehension and computational analysis. Also, we can not directly apply statistical learning models in data science to a set of phylogenetic trees since the space of phylogenetic trees is not Euclidean. In fact, the space of phylogenetic trees is a tropical Grassmannian in terms of max-plus algebra. Therefore, to classify multi-locus data sets for phylogenetic analysis, we propose tropical support vector machines (SVMs). Like classical SVMs, a tropical SVM is a discriminative classifier defined by the tropical hyperplane which maximizes the minimum tropical distance from data points to itself in order to separate these data points into sectors (half-spaces) in the tropical projective torus. Both hard margin tropical SVMs and soft margin tropical SVMs can be formulated as linear programming problems. We focus on classifying two categories of data, and we study a simpler case by assuming the data points from the same category ideally stay in the same sector of a tropical separating hyperplane. For hard margin tropical SVMs, we prove the necessary and sufficient conditions for two categories of data points to be separated, and we show an explicit formula for the optimal value of the feasible linear programming problem. For soft margin tropical SVMs, we develop novel methods to compute an optimal tropical separating hyperplane. Computational experiments show our methods work well. We end this paper with open problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge