Beyond Discriminative Regions: Saliency Maps as Alternatives to CAMs for Weakly Supervised Semantic Segmentation

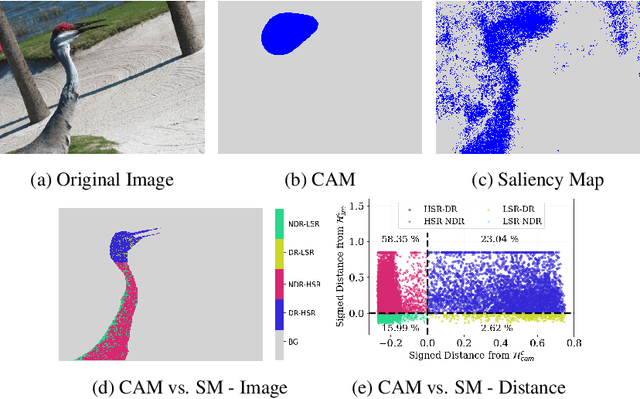
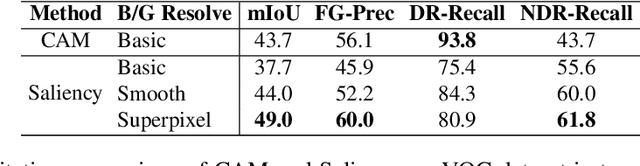
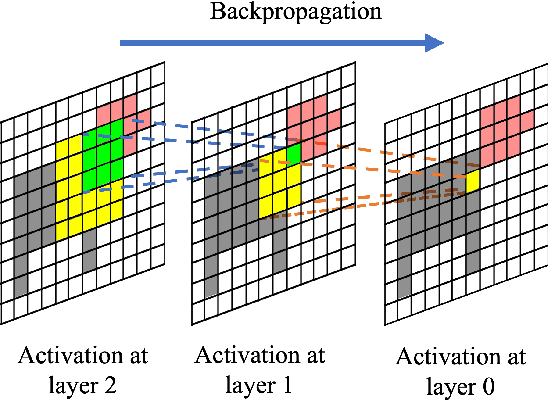
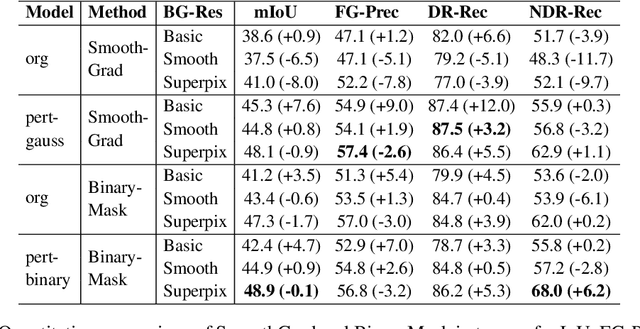
In recent years, several Weakly Supervised Semantic Segmentation (WS3) methods have been proposed that use class activation maps (CAMs) generated by a classifier to produce pseudo-ground truths for training segmentation models. While CAMs are good at highlighting discriminative regions (DR) of an image, they are known to disregard regions of the object that do not contribute to the classifier's prediction, termed non-discriminative regions (NDR). In contrast, attribution methods such as saliency maps provide an alternative approach for assigning a score to every pixel based on its contribution to the classification prediction. This paper provides a comprehensive comparison between saliencies and CAMs for WS3. Our study includes multiple perspectives on understanding their similarities and dissimilarities. Moreover, we provide new evaluation metrics that perform a comprehensive assessment of WS3 performance of alternative methods w.r.t. CAMs. We demonstrate the effectiveness of saliencies in addressing the limitation of CAMs through our empirical studies on benchmark datasets. Furthermore, we propose random cropping as a stochastic aggregation technique that improves the performance of saliency, making it a strong alternative to CAM for WS3.

Let There Be Order: Rethinking Ordering in Autoregressive Graph Generation

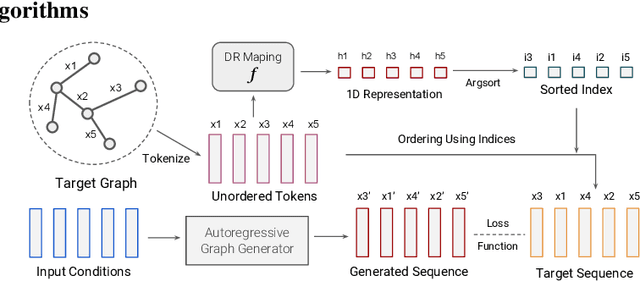
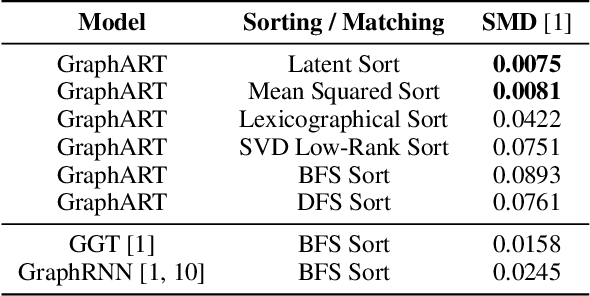
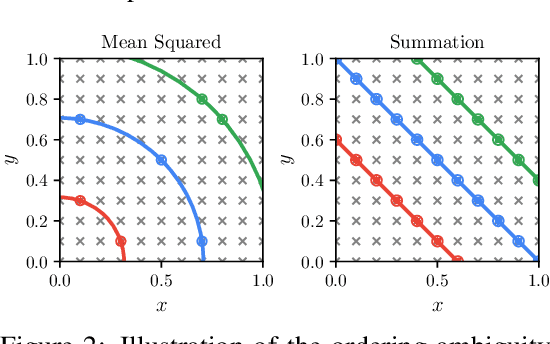
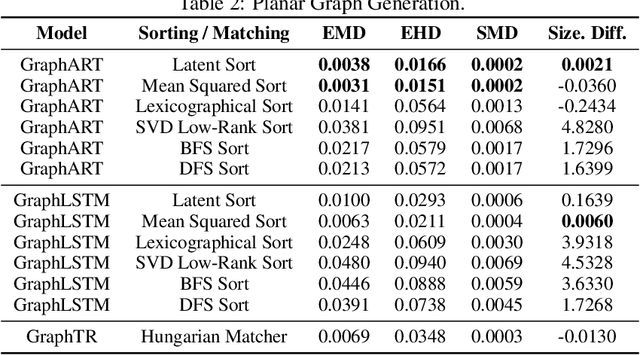
Conditional graph generation tasks involve training a model to generate a graph given a set of input conditions. Many previous studies employ autoregressive models to incrementally generate graph components such as nodes and edges. However, as graphs typically lack a natural ordering among their components, converting a graph into a sequence of tokens is not straightforward. While prior works mostly rely on conventional heuristics or graph traversal methods like breadth-first search (BFS) or depth-first search (DFS) to convert graphs to sequences, the impact of ordering on graph generation has largely been unexplored. This paper contributes to this problem by: (1) highlighting the crucial role of ordering in autoregressive graph generation models, (2) proposing a novel theoretical framework that perceives ordering as a dimensionality reduction problem, thereby facilitating a deeper understanding of the relationship between orderings and generated graph accuracy, and (3) introducing "latent sort," a learning-based ordering scheme to perform dimensionality reduction of graph tokens. Our experimental results showcase the effectiveness of latent sort across a wide range of graph generation tasks, encouraging future works to further explore and develop learning-based ordering schemes for autoregressive graph generation.

Rethinking the Importance of Sampling in Physics-informed Neural Networks

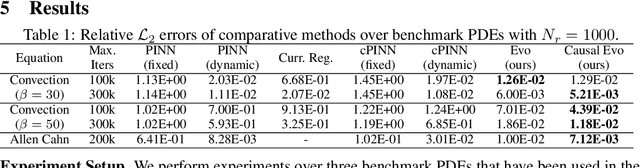
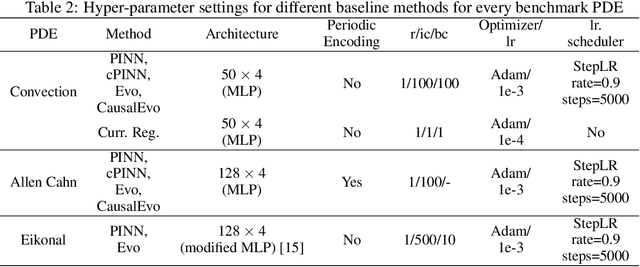
Physics-informed neural networks (PINNs) have emerged as a powerful tool for solving partial differential equations (PDEs) in a variety of domains. While previous research in PINNs has mainly focused on constructing and balancing loss functions during training to avoid poor minima, the effect of sampling collocation points on the performance of PINNs has largely been overlooked. In this work, we find that the performance of PINNs can vary significantly with different sampling strategies, and using a fixed set of collocation points can be quite detrimental to the convergence of PINNs to the correct solution. In particular, (1) we hypothesize that training of PINNs rely on successful "propagation" of solution from initial and/or boundary condition points to interior points, and PINNs with poor sampling strategies can get stuck at trivial solutions if there are \textit{propagation failures}. (2) We demonstrate that propagation failures are characterized by highly imbalanced PDE residual fields where very high residuals are observed over very narrow regions. (3) To mitigate propagation failure, we propose a novel \textit{evolutionary sampling} (Evo) method that can incrementally accumulate collocation points in regions of high PDE residuals. We further provide an extension of Evo to respect the principle of causality while solving time-dependent PDEs. We empirically demonstrate the efficacy and efficiency of our proposed methods in a variety of PDE problems.

Learning Compact Representations of Neural Networks using DiscriminAtive Masking (DAM)

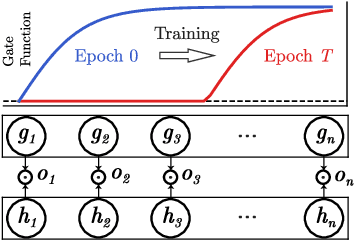
A central goal in deep learning is to learn compact representations of features at every layer of a neural network, which is useful for both unsupervised representation learning and structured network pruning. While there is a growing body of work in structured pruning, current state-of-the-art methods suffer from two key limitations: (i) instability during training, and (ii) need for an additional step of fine-tuning, which is resource-intensive. At the core of these limitations is the lack of a systematic approach that jointly prunes and refines weights during training in a single stage, and does not require any fine-tuning upon convergence to achieve state-of-the-art performance. We present a novel single-stage structured pruning method termed DiscriminAtive Masking (DAM). The key intuition behind DAM is to discriminatively prefer some of the neurons to be refined during the training process, while gradually masking out other neurons. We show that our proposed DAM approach has remarkably good performance over various applications, including dimensionality reduction, recommendation system, graph representation learning, and structured pruning for image classification. We also theoretically show that the learning objective of DAM is directly related to minimizing the L0 norm of the masking layer.

Quadratic Residual Networks: A New Class of Neural Networks for Solving Forward and Inverse Problems in Physics Involving PDEs

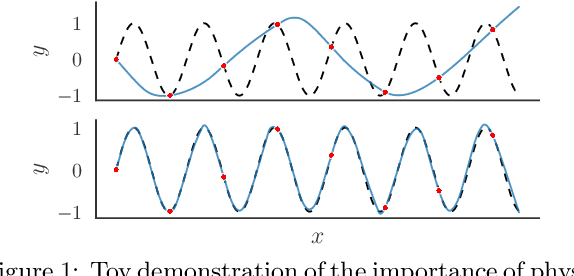
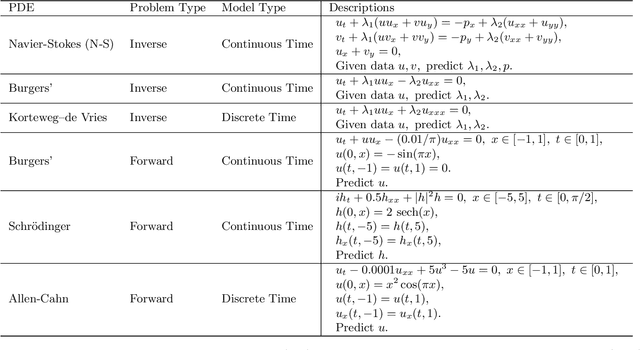
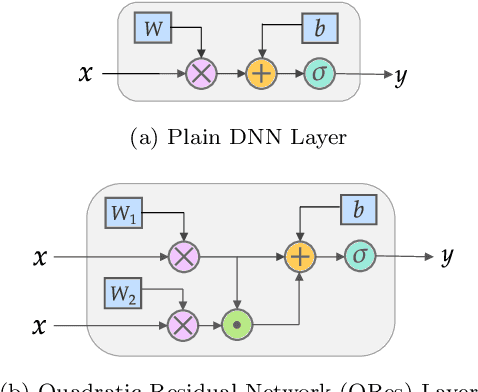
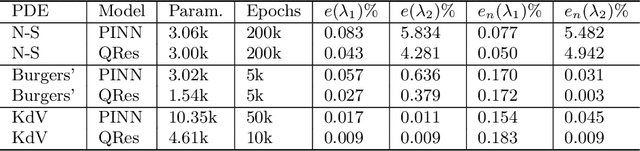
We propose quadratic residual networks (QRes) as a new type of parameter-efficient neural network architecture, by adding a quadratic residual term to the weighted sum of inputs before applying activation functions. With sufficiently high functional capacity (or expressive power), we show that it is especially powerful for solving forward and inverse physics problems involving partial differential equations (PDEs). Using tools from algebraic geometry, we theoretically demonstrate that, in contrast to plain neural networks, QRes shows better parameter efficiency in terms of network width and depth thanks to higher non-linearity in every neuron. Finally, we empirically show that QRes shows faster convergence speed in terms of number of training epochs especially in learning complex patterns.

Beyond Observed Connections : Link Injection

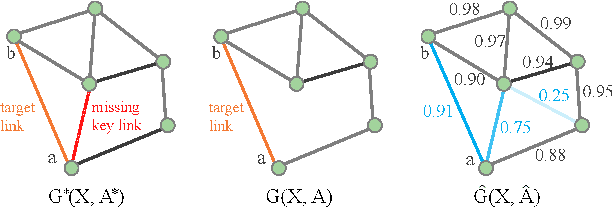
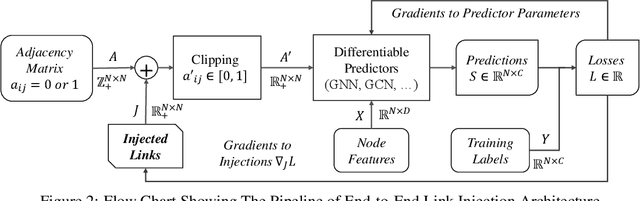
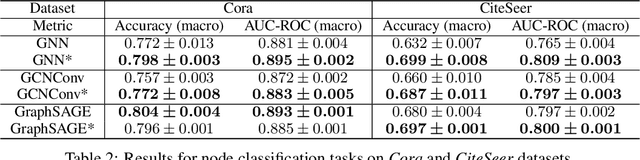
In this paper, we proposed the \textit{link injection}, a novel method that helps any differentiable graph machine learning models to go beyond observed connections from the input data in an end-to-end learning fashion. It finds out (weak) connections in favor of the current task that is not present in the input data via a parametric link injection layer. We evaluate our method on both node classification and link prediction tasks using a series of state-of-the-art graph convolution networks. Results show that the link injection helps a variety of models to achieve better performances on both applications. Further empirical analysis shows a great potential of this method in efficiently exploiting unseen connections from the injected links.

Learning Neural Networks with Competing Physics Objectives: An Application in Quantum Mechanics

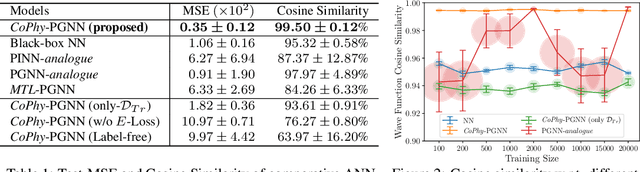
Physics-guided Machine Learning (PGML) is an emerging field of research in machine learning (ML) that aims to harness the power of ML advances without ignoring the rich knowledge of physics underlying scientific phenomena. One of the promising directions in PGML is to modify the objective function of neural networks by adding physics-guided (PG) loss functions that measure the violation of physics objectives in the ANN outputs. Existing PGML approaches generally focus on incorporating a single physics objective as a PG loss, using constant trade-off parameters. However, in the presence of multiple physics objectives with competing non-convex PG loss terms, there is a need to adaptively tune the importance of competing PG loss terms during the process of neural network training. We present a novel approach to handle competing PG loss terms in the illustrative application of quantum mechanics, where the two competing physics objectives are minimizing the energy while satisfying the Schrodinger equation. We conducted a systematic evaluation of the effects of PG loss on the generalization ability of neural networks in comparison with several baseline methods in PGML. All the code and data used in this work is available at https://github.com/jayroxis/Cophy-PGNN.

Physics-guided Design and Learning of Neural Networks for Predicting Drag Force on Particle Suspensions in Moving Fluids

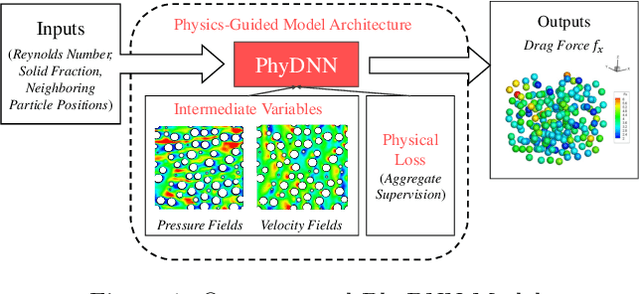
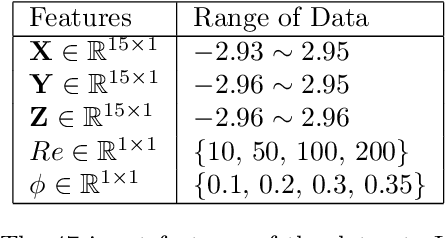
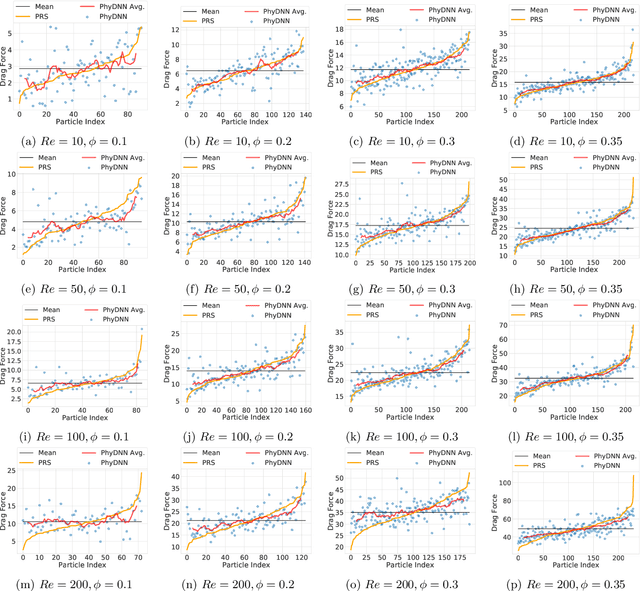
Physics-based simulations are often used to model and understand complex physical systems and processes in domains like fluid dynamics. Such simulations, although used frequently, have many limitations which could arise either due to the inability to accurately model a physical process owing to incomplete knowledge about certain facets of the process or due to the underlying process being too complex to accurately encode into a simulation model. In such situations, it is often useful to rely on machine learning methods to fill in the gap by learning a model of the complex physical process directly from simulation data. However, as data generation through simulations is costly, we need to develop models, being cognizant of data paucity issues. In such scenarios it is often helpful if the rich physical knowledge of the application domain is incorporated in the architectural design of machine learning models. Further, we can also use information from physics-based simulations to guide the learning process using aggregate supervision to favorably constrain the learning process. In this paper, we propose PhyDNN, a deep learning model using physics-guided structural priors and physics-guided aggregate supervision for modeling the drag forces acting on each particle in a Computational Fluid Dynamics-Discrete Element Method(CFD-DEM). We conduct extensive experiments in the context of drag force prediction and showcase the usefulness of including physics knowledge in our deep learning formulation both in the design and through learning process. Our proposed PhyDNN model has been compared to several state-of-the-art models and achieves a significant performance improvement of 8.46% on average across all baseline models. The source code has been made available and the dataset used is detailed in [1, 2].