Physics-Guided Problem Decomposition for Scaling Deep Learning of High-dimensional Eigen-Solvers: The Case of Schrödinger's Equation

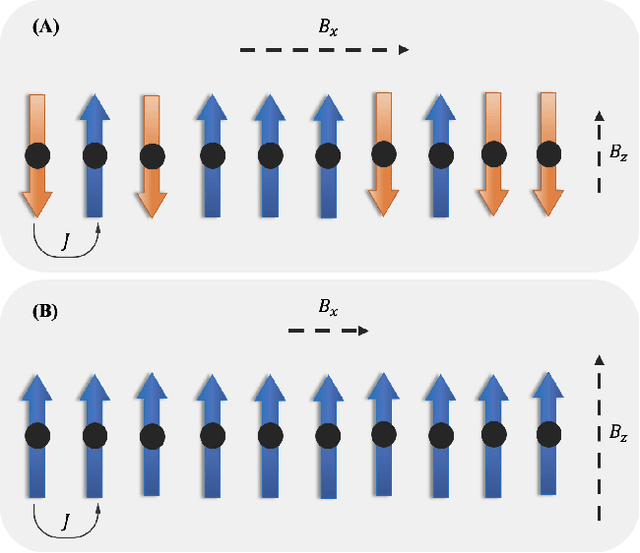
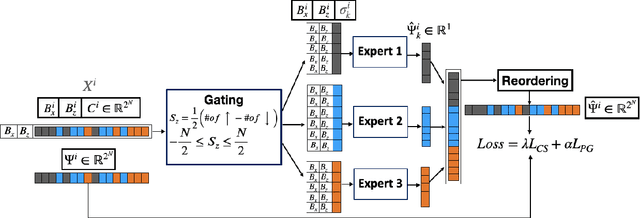
Given their ability to effectively learn non-linear mappings and perform fast inference, deep neural networks (NNs) have been proposed as a viable alternative to traditional simulation-driven approaches for solving high-dimensional eigenvalue equations (HDEs), which are the foundation for many scientific applications. Unfortunately, for the learned models in these scientific applications to achieve generalization, a large, diverse, and preferably annotated dataset is typically needed and is computationally expensive to obtain. Furthermore, the learned models tend to be memory- and compute-intensive primarily due to the size of the output layer. While generalization, especially extrapolation, with scarce data has been attempted by imposing physical constraints in the form of physics loss, the problem of model scalability has remained. In this paper, we alleviate the compute bottleneck in the output layer by using physics knowledge to decompose the complex regression task of predicting the high-dimensional eigenvectors into multiple simpler sub-tasks, each of which are learned by a simple "expert" network. We call the resulting architecture of specialized experts Physics-Guided Mixture-of-Experts (PG-MoE). We demonstrate the efficacy of such physics-guided problem decomposition for the case of the Schr\"{o}dinger's Equation in Quantum Mechanics. Our proposed PG-MoE model predicts the ground-state solution, i.e., the eigenvector that corresponds to the smallest possible eigenvalue. The model is 150x smaller than the network trained to learn the complex task while being competitive in generalization. To improve the generalization of the PG-MoE, we also employ a physics-guided loss function based on variational energy, which by quantum mechanics principles is minimized iff the output is the ground-state solution.

Learning Neural Networks with Competing Physics Objectives: An Application in Quantum Mechanics

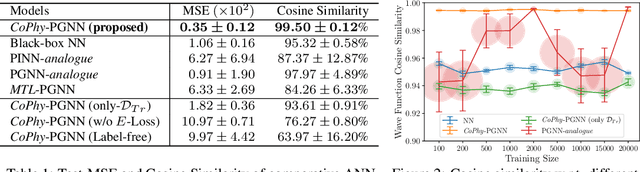
Physics-guided Machine Learning (PGML) is an emerging field of research in machine learning (ML) that aims to harness the power of ML advances without ignoring the rich knowledge of physics underlying scientific phenomena. One of the promising directions in PGML is to modify the objective function of neural networks by adding physics-guided (PG) loss functions that measure the violation of physics objectives in the ANN outputs. Existing PGML approaches generally focus on incorporating a single physics objective as a PG loss, using constant trade-off parameters. However, in the presence of multiple physics objectives with competing non-convex PG loss terms, there is a need to adaptively tune the importance of competing PG loss terms during the process of neural network training. We present a novel approach to handle competing PG loss terms in the illustrative application of quantum mechanics, where the two competing physics objectives are minimizing the energy while satisfying the Schrodinger equation. We conducted a systematic evaluation of the effects of PG loss on the generalization ability of neural networks in comparison with several baseline methods in PGML. All the code and data used in this work is available at https://github.com/jayroxis/Cophy-PGNN.