Christopher Singh
Learning Neural Networks with Competing Physics Objectives: An Application in Quantum Mechanics
Jul 02, 2020
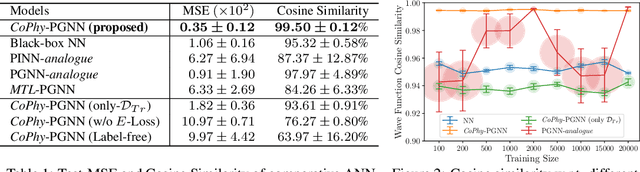


Abstract:Physics-guided Machine Learning (PGML) is an emerging field of research in machine learning (ML) that aims to harness the power of ML advances without ignoring the rich knowledge of physics underlying scientific phenomena. One of the promising directions in PGML is to modify the objective function of neural networks by adding physics-guided (PG) loss functions that measure the violation of physics objectives in the ANN outputs. Existing PGML approaches generally focus on incorporating a single physics objective as a PG loss, using constant trade-off parameters. However, in the presence of multiple physics objectives with competing non-convex PG loss terms, there is a need to adaptively tune the importance of competing PG loss terms during the process of neural network training. We present a novel approach to handle competing PG loss terms in the illustrative application of quantum mechanics, where the two competing physics objectives are minimizing the energy while satisfying the Schrodinger equation. We conducted a systematic evaluation of the effects of PG loss on the generalization ability of neural networks in comparison with several baseline methods in PGML. All the code and data used in this work is available at https://github.com/jayroxis/Cophy-PGNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge