Graph Pre-Training Models Are Strong Anomaly Detectors

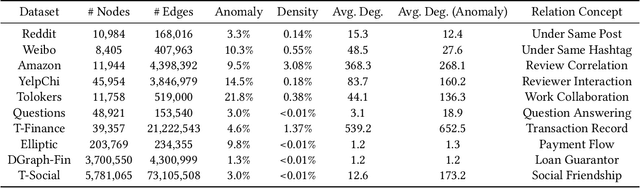
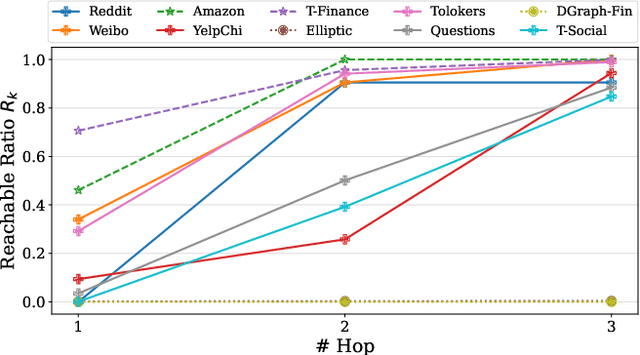
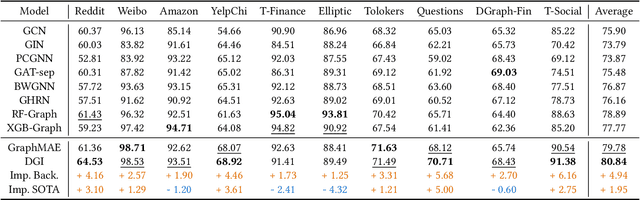
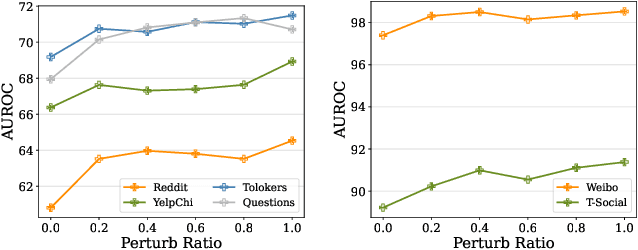
Graph Anomaly Detection (GAD) is a challenging and practical research topic where Graph Neural Networks (GNNs) have recently shown promising results. The effectiveness of existing GNNs in GAD has been mainly attributed to the simultaneous learning of node representations and the classifier in an end-to-end manner. Meanwhile, graph pre-training, the two-stage learning paradigm such as DGI and GraphMAE, has shown potential in leveraging unlabeled graph data to enhance downstream tasks, yet its impact on GAD remains under-explored. In this work, we show that graph pre-training models are strong graph anomaly detectors. Specifically, we demonstrate that pre-training is highly competitive, markedly outperforming the state-of-the-art end-to-end training models when faced with limited supervision. To understand this phenomenon, we further uncover pre-training enhances the detection of distant, under-represented, unlabeled anomalies that go beyond 2-hop neighborhoods of known anomalies, shedding light on its superior performance against end-to-end models. Moreover, we extend our examination to the potential of pre-training in graph-level anomaly detection. We envision this work to stimulate a re-evaluation of pre-training's role in GAD and offer valuable insights for future research.

Deep Insights into Noisy Pseudo Labeling on Graph Data

Pseudo labeling (PL) is a wide-applied strategy to enlarge the labeled dataset by self-annotating the potential samples during the training process. Several works have shown that it can improve the graph learning model performance in general. However, we notice that the incorrect labels can be fatal to the graph training process. Inappropriate PL may result in the performance degrading, especially on graph data where the noise can propagate. Surprisingly, the corresponding error is seldom theoretically analyzed in the literature. In this paper, we aim to give deep insights of PL on graph learning models. We first present the error analysis of PL strategy by showing that the error is bounded by the confidence of PL threshold and consistency of multi-view prediction. Then, we theoretically illustrate the effect of PL on convergence property. Based on the analysis, we propose a cautious pseudo labeling methodology in which we pseudo label the samples with highest confidence and multi-view consistency. Finally, extensive experiments demonstrate that the proposed strategy improves graph learning process and outperforms other PL strategies on link prediction and node classification tasks.

Physics-Inspired Neural Graph ODE for Long-term Dynamical Simulation

Simulating and modeling the long-term dynamics of multi-object physical systems is an essential and challenging task. Current studies model the physical systems utilizing Graph Neural Networks (GNNs) with equivariant properties. Specifically, they model the dynamics as a sequence of discrete states with a fixed time interval and learn a direct mapping for all the two adjacent states. However, this direct mapping overlooks the continuous nature between the two states. Namely, we have verified that there are countless possible trajectories between two discrete dynamic states in current GNN-based direct mapping models. This issue greatly hinders the model generalization ability, leading to poor performance of the long-term simulation. In this paper, to better model the latent trajectory through discrete supervision signals, we propose a Physics-Inspired Neural Graph ODE (PINGO) algorithm. In PINGO, to ensure the uniqueness of the trajectory, we construct a Physics-Inspired Neural ODE framework to update the latent trajectory. Meanwhile, to effectively capture intricate interactions among objects, we use a GNN-based model to parameterize Neural ODE in a plug-and-play manner. Furthermore, we prove that the discrepancy between the learned trajectory of PIGNO and the true trajectory can be theoretically bounded. Extensive experiments verify our theoretical findings and demonstrate that our model yields an order-of-magnitude improvement over the state-of-the-art baselines, especially on long-term predictions and roll-out errors.

Handling Missing Data via Max-Entropy Regularized Graph Autoencoder

Graph neural networks (GNNs) are popular weapons for modeling relational data. Existing GNNs are not specified for attribute-incomplete graphs, making missing attribute imputation a burning issue. Until recently, many works notice that GNNs are coupled with spectral concentration, which means the spectrum obtained by GNNs concentrates on a local part in spectral domain, e.g., low-frequency due to oversmoothing issue. As a consequence, GNNs may be seriously flawed for reconstructing graph attributes as graph spectral concentration tends to cause a low imputation precision. In this work, we present a regularized graph autoencoder for graph attribute imputation, named MEGAE, which aims at mitigating spectral concentration problem by maximizing the graph spectral entropy. Notably, we first present the method for estimating graph spectral entropy without the eigen-decomposition of Laplacian matrix and provide the theoretical upper error bound. A maximum entropy regularization then acts in the latent space, which directly increases the graph spectral entropy. Extensive experiments show that MEGAE outperforms all the other state-of-the-art imputation methods on a variety of benchmark datasets.

Latent Augmentation Improves Graph Self-Supervised Learning

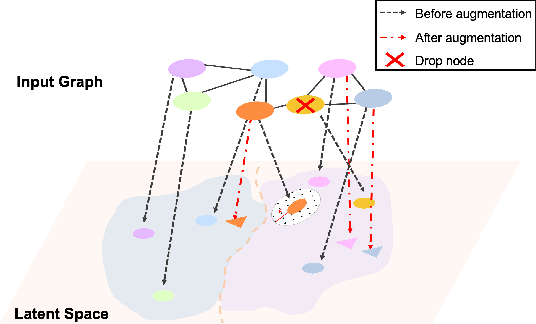
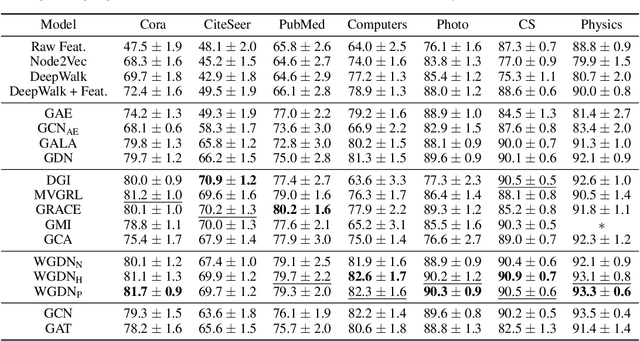
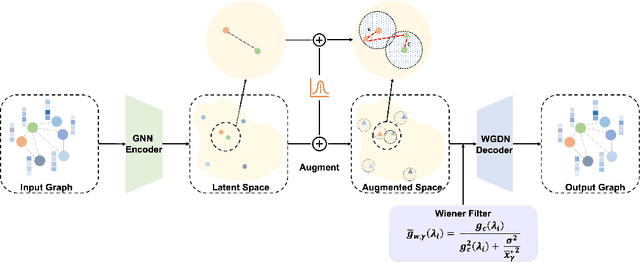
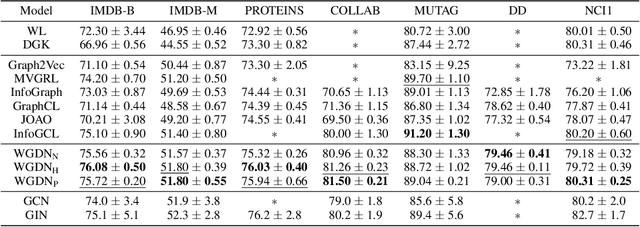
Graph self-supervised learning has been vastly employed to learn representations from unlabeled graphs. Existing methods can be roughly divided into predictive learning and contrastive learning, where the latter one attracts more research attention with better empirical performance. We argue that, however, predictive models weaponed with latent augmentations and powerful decoder could achieve comparable or even better representation power than contrastive models. In this work, we introduce data augmentations into latent space for superior generalization and better efficiency. A novel graph decoder named Wiener Graph Deconvolutional Network is correspondingly designed to perform information reconstruction from augmented latent representations. Theoretical analysis proves the superior reconstruction ability of graph wiener filter. Extensive experimental results on various datasets demonstrate the effectiveness of our approach.