Graph Pre-Training Models Are Strong Anomaly Detectors

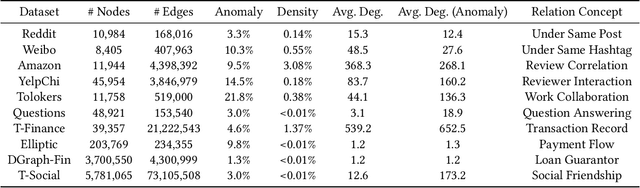
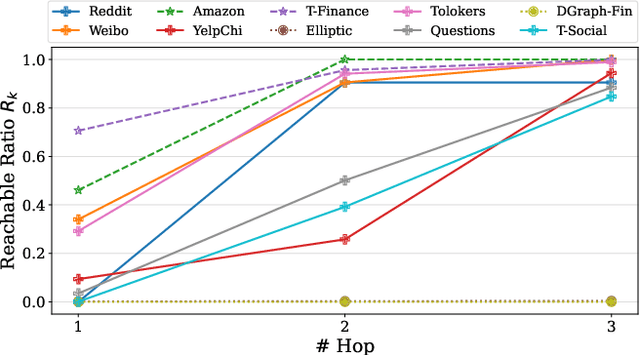
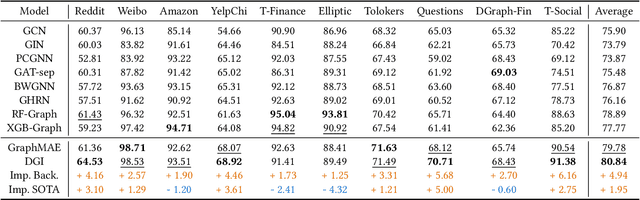
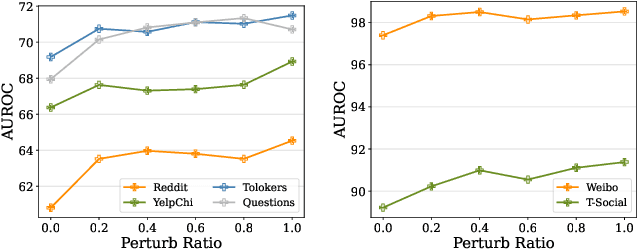
Graph Anomaly Detection (GAD) is a challenging and practical research topic where Graph Neural Networks (GNNs) have recently shown promising results. The effectiveness of existing GNNs in GAD has been mainly attributed to the simultaneous learning of node representations and the classifier in an end-to-end manner. Meanwhile, graph pre-training, the two-stage learning paradigm such as DGI and GraphMAE, has shown potential in leveraging unlabeled graph data to enhance downstream tasks, yet its impact on GAD remains under-explored. In this work, we show that graph pre-training models are strong graph anomaly detectors. Specifically, we demonstrate that pre-training is highly competitive, markedly outperforming the state-of-the-art end-to-end training models when faced with limited supervision. To understand this phenomenon, we further uncover pre-training enhances the detection of distant, under-represented, unlabeled anomalies that go beyond 2-hop neighborhoods of known anomalies, shedding light on its superior performance against end-to-end models. Moreover, we extend our examination to the potential of pre-training in graph-level anomaly detection. We envision this work to stimulate a re-evaluation of pre-training's role in GAD and offer valuable insights for future research.

Relaxing Continuous Constraints of Equivariant Graph Neural Networks for Physical Dynamics Learning

Incorporating Euclidean symmetries (e.g. rotation equivariance) as inductive biases into graph neural networks has improved their generalization ability and data efficiency in unbounded physical dynamics modeling. However, in various scientific and engineering applications, the symmetries of dynamics are frequently discrete due to the boundary conditions. Thus, existing GNNs either overlook necessary symmetry, resulting in suboptimal representation ability, or impose excessive equivariance, which fails to generalize to unobserved symmetric dynamics. In this work, we propose a general Discrete Equivariant Graph Neural Network (DEGNN) that guarantees equivariance to a given discrete point group. Specifically, we show that such discrete equivariant message passing could be constructed by transforming geometric features into permutation-invariant embeddings. Through relaxing continuous equivariant constraints, DEGNN can employ more geometric feature combinations to approximate unobserved physical object interaction functions. Two implementation approaches of DEGNN are proposed based on ranking or pooling permutation-invariant functions. We apply DEGNN to various physical dynamics, ranging from particle, molecular, crowd to vehicle dynamics. In twenty scenarios, DEGNN significantly outperforms existing state-of-the-art approaches. Moreover, we show that DEGNN is data efficient, learning with less data, and can generalize across scenarios such as unobserved orientation.

Breaking Language Barriers in Multilingual Mathematical Reasoning: Insights and Observations

Existing research predominantly focuses on developing powerful language learning models (LLMs) for mathematical reasoning within monolingual languages, with few explorations in preserving efficacy in a multilingual context. To bridge this gap, this paper pioneers exploring and training powerful Multilingual Math Reasoning (xMR) LLMs. Firstly, by utilizing translation, we construct the first multilingual math reasoning instruction dataset, MGSM8KInstruct, encompassing ten distinct languages, thus addressing the issue of training data scarcity in xMR tasks. Based on the collected dataset, we propose different training strategies to build powerful xMR LLMs, named MathOctopus, notably outperform conventional open-source LLMs and exhibit superiority over ChatGPT in few-shot scenarios. Notably, MathOctopus-13B reaches 47.6% accuracy which exceeds ChatGPT 46.3% on MGSM testset. Beyond remarkable results, we unearth several pivotal observations and insights from extensive experiments: (1) When extending the rejection sampling strategy to the multilingual context, it proves effective for model performances, albeit limited. (2) Employing parallel corpora for math Supervised Fine-Tuning (SFT) across multiple languages not only significantly enhances model performance multilingually but also elevates their monolingual performance. This indicates that crafting multilingual corpora can be regarded as a vital strategy for enhancing model performance in a specific language, especially in mathematical reasoning tasks. For instance, MathOctopus-7B improves its counterparts that trained on English from 42.2% to 50.8% on GSM8K testset.