Jeremy Appleyard
Morphology-preserving Autoregressive 3D Generative Modelling of the Brain
Sep 07, 2022
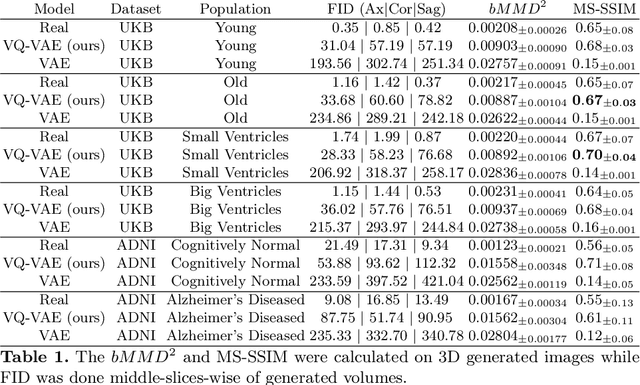
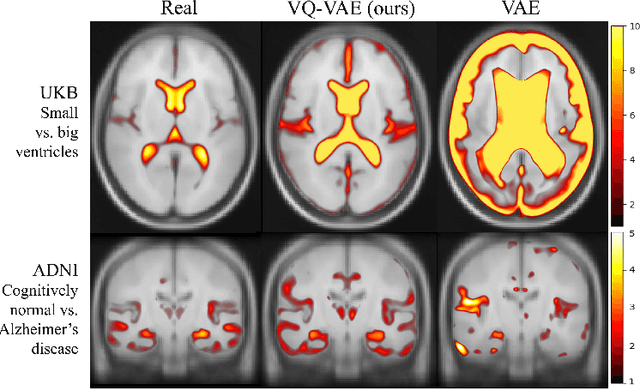
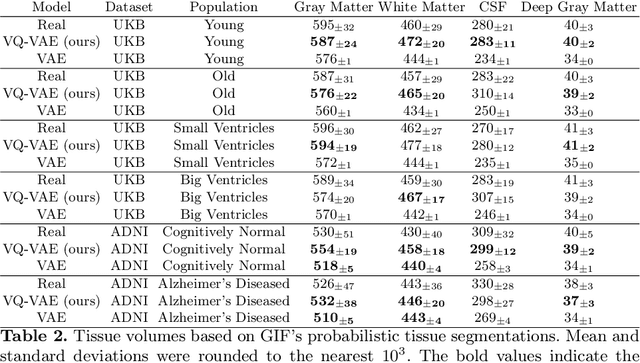
Abstract:Human anatomy, morphology, and associated diseases can be studied using medical imaging data. However, access to medical imaging data is restricted by governance and privacy concerns, data ownership, and the cost of acquisition, thus limiting our ability to understand the human body. A possible solution to this issue is the creation of a model able to learn and then generate synthetic images of the human body conditioned on specific characteristics of relevance (e.g., age, sex, and disease status). Deep generative models, in the form of neural networks, have been recently used to create synthetic 2D images of natural scenes. Still, the ability to produce high-resolution 3D volumetric imaging data with correct anatomical morphology has been hampered by data scarcity and algorithmic and computational limitations. This work proposes a generative model that can be scaled to produce anatomically correct, high-resolution, and realistic images of the human brain, with the necessary quality to allow further downstream analyses. The ability to generate a potentially unlimited amount of data not only enables large-scale studies of human anatomy and pathology without jeopardizing patient privacy, but also significantly advances research in the field of anomaly detection, modality synthesis, learning under limited data, and fair and ethical AI. Code and trained models are available at: https://github.com/AmigoLab/SynthAnatomy.
Sparse Persistent RNNs: Squeezing Large Recurrent Networks On-Chip
Apr 26, 2018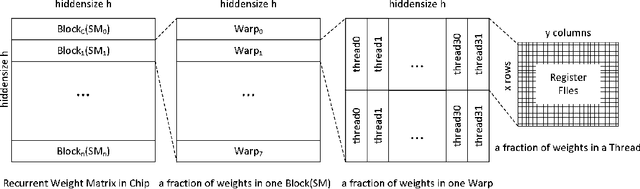
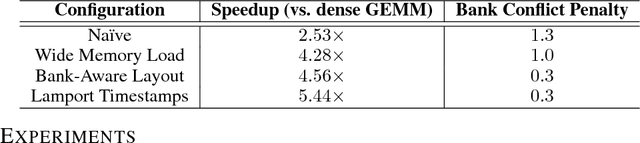
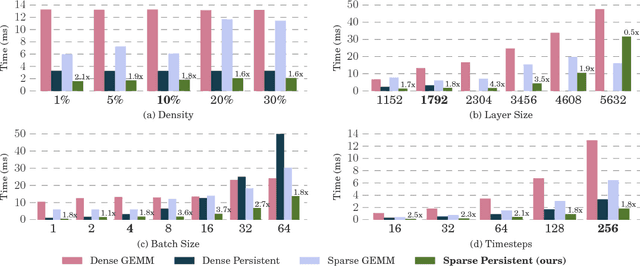
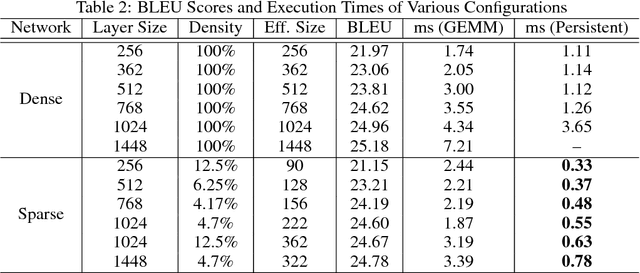
Abstract:Recurrent Neural Networks (RNNs) are powerful tools for solving sequence-based problems, but their efficacy and execution time are dependent on the size of the network. Following recent work in simplifying these networks with model pruning and a novel mapping of work onto GPUs, we design an efficient implementation for sparse RNNs. We investigate several optimizations and tradeoffs: Lamport timestamps, wide memory loads, and a bank-aware weight layout. With these optimizations, we achieve speedups of over 6x over the next best algorithm for a hidden layer of size 2304, batch size of 4, and a density of 30%. Further, our technique allows for models of over 5x the size to fit on a GPU for a speedup of 2x, enabling larger networks to help advance the state-of-the-art. We perform case studies on NMT and speech recognition tasks in the appendix, accelerating their recurrent layers by up to 3x.
Optimizing Performance of Recurrent Neural Networks on GPUs
Apr 07, 2016


Abstract:As recurrent neural networks become larger and deeper, training times for single networks are rising into weeks or even months. As such there is a significant incentive to improve the performance and scalability of these networks. While GPUs have become the hardware of choice for training and deploying recurrent models, the implementations employed often make use of only basic optimizations for these architectures. In this article we demonstrate that by exposing parallelism between operations within the network, an order of magnitude speedup across a range of network sizes can be achieved over a naive implementation. We describe three stages of optimization that have been incorporated into the fifth release of NVIDIA's cuDNN: firstly optimizing a single cell, secondly a single layer, and thirdly the entire network.
ACDC: A Structured Efficient Linear Layer
Mar 19, 2016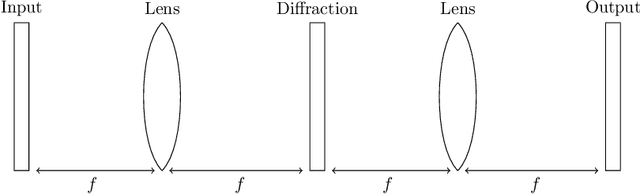
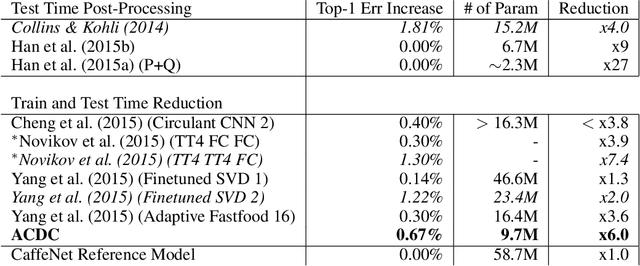
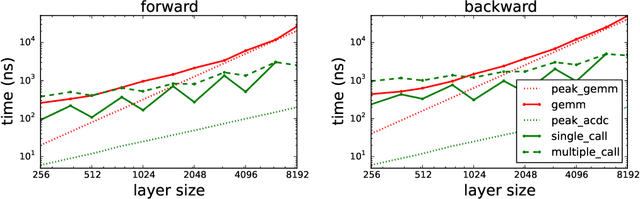
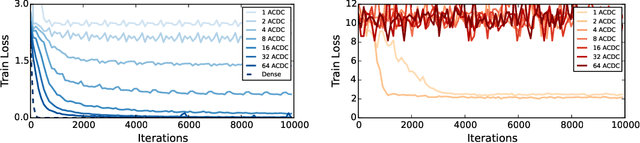
Abstract:The linear layer is one of the most pervasive modules in deep learning representations. However, it requires $O(N^2)$ parameters and $O(N^2)$ operations. These costs can be prohibitive in mobile applications or prevent scaling in many domains. Here, we introduce a deep, differentiable, fully-connected neural network module composed of diagonal matrices of parameters, $\mathbf{A}$ and $\mathbf{D}$, and the discrete cosine transform $\mathbf{C}$. The core module, structured as $\mathbf{ACDC^{-1}}$, has $O(N)$ parameters and incurs $O(N log N )$ operations. We present theoretical results showing how deep cascades of ACDC layers approximate linear layers. ACDC is, however, a stand-alone module and can be used in combination with any other types of module. In our experiments, we show that it can indeed be successfully interleaved with ReLU modules in convolutional neural networks for image recognition. Our experiments also study critical factors in the training of these structured modules, including initialization and depth. Finally, this paper also provides a connection between structured linear transforms used in deep learning and the field of Fourier optics, illustrating how ACDC could in principle be implemented with lenses and diffractive elements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge