ACDC: A Structured Efficient Linear Layer
Paper and Code
Mar 19, 2016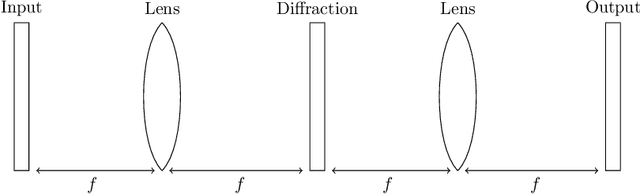
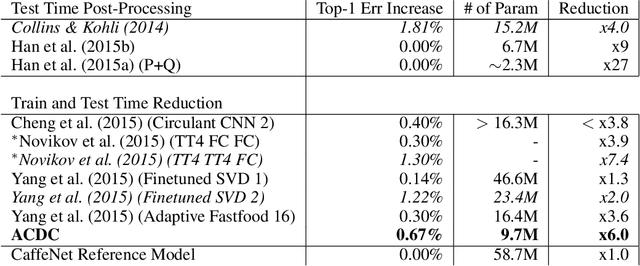
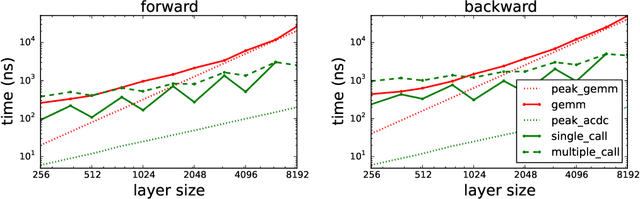
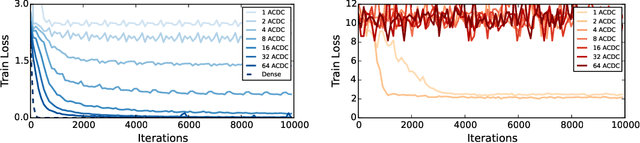
The linear layer is one of the most pervasive modules in deep learning representations. However, it requires $O(N^2)$ parameters and $O(N^2)$ operations. These costs can be prohibitive in mobile applications or prevent scaling in many domains. Here, we introduce a deep, differentiable, fully-connected neural network module composed of diagonal matrices of parameters, $\mathbf{A}$ and $\mathbf{D}$, and the discrete cosine transform $\mathbf{C}$. The core module, structured as $\mathbf{ACDC^{-1}}$, has $O(N)$ parameters and incurs $O(N log N )$ operations. We present theoretical results showing how deep cascades of ACDC layers approximate linear layers. ACDC is, however, a stand-alone module and can be used in combination with any other types of module. In our experiments, we show that it can indeed be successfully interleaved with ReLU modules in convolutional neural networks for image recognition. Our experiments also study critical factors in the training of these structured modules, including initialization and depth. Finally, this paper also provides a connection between structured linear transforms used in deep learning and the field of Fourier optics, illustrating how ACDC could in principle be implemented with lenses and diffractive elements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge