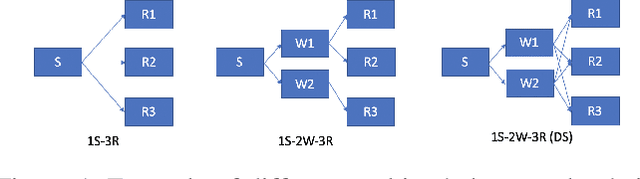
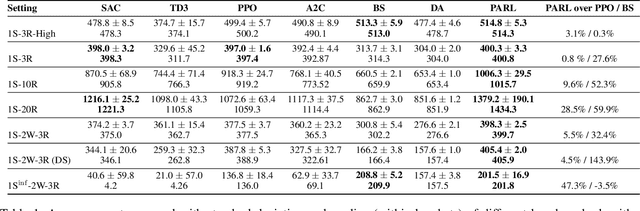
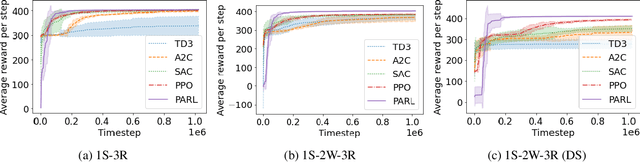
Math Programming based Reinforcement Learning for Multi-Echelon Inventory Management

Reinforcement learning has lead to considerable break-throughs in diverse areas such as robotics, games and many others. But the application to RL in complex real-world decision making problems remains limited. Many problems in operations management (inventory and revenue management, for example) are characterized by large action spaces and stochastic system dynamics. These characteristics make the problem considerably harder to solve for existing RL methods that rely on enumeration techniques to solve per step action problems. To resolve these issues, we develop Programmable Actor Reinforcement Learning (PARL), a policy iteration method that uses techniques from integer programming and sample average approximation. Analytically, we show that the for a given critic, the learned policy in each iteration converges to the optimal policy as the underlying samples of the uncertainty go to infinity. Practically, we show that a properly selected discretization of the underlying uncertain distribution can yield near optimal actor policy even with very few samples from the underlying uncertainty. We then apply our algorithm to real-world inventory management problems with complex supply chain structures and show that PARL outperforms state-of-the-art RL and inventory optimization methods in these settings. We find that PARL outperforms commonly used base stock heuristic by 44.7% and the best performing RL method by up to 12.1% on average across different supply chain environments.

A Scalable MIP-based Method for Learning Optimal Multivariate Decision Trees

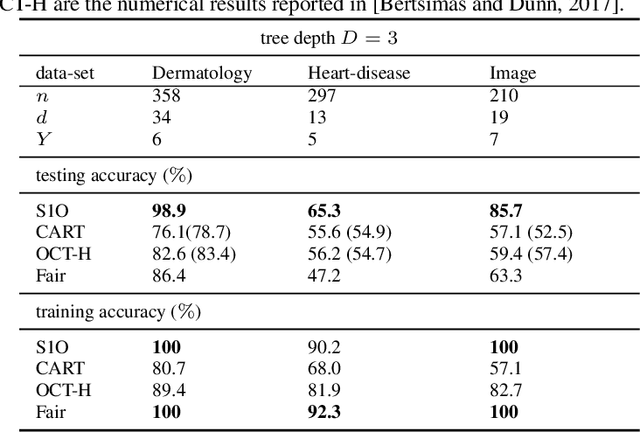
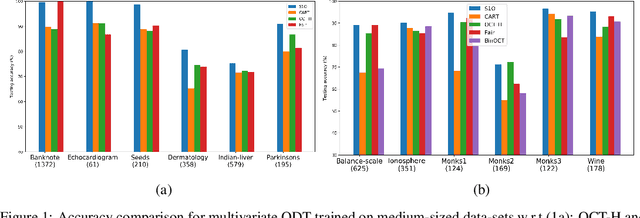
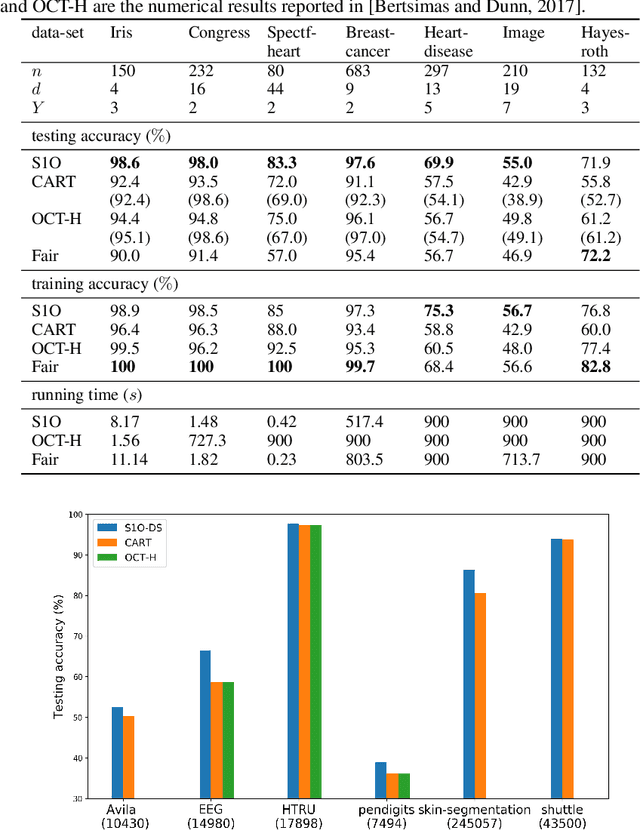
Several recent publications report advances in training optimal decision trees (ODT) using mixed-integer programs (MIP), due to algorithmic advances in integer programming and a growing interest in addressing the inherent suboptimality of heuristic approaches such as CART. In this paper, we propose a novel MIP formulation, based on a 1-norm support vector machine model, to train a multivariate ODT for classification problems. We provide cutting plane techniques that tighten the linear relaxation of the MIP formulation, in order to improve run times to reach optimality. Using 36 data-sets from the University of California Irvine Machine Learning Repository, we demonstrate that our formulation outperforms its counterparts in the literature by an average of about 10% in terms of mean out-of-sample testing accuracy across the data-sets. We provide a scalable framework to train multivariate ODT on large data-sets by introducing a novel linear programming (LP) based data selection method to choose a subset of the data for training. Our method is able to routinely handle large data-sets with more than 7,000 sample points and outperform heuristics methods and other MIP based techniques. We present results on data-sets containing up to 245,000 samples. Existing MIP-based methods do not scale well on training data-sets beyond 5,500 samples.

Variational inference formulation for a model-free simulation of a dynamical system with unknown parameters by a recurrent neural network

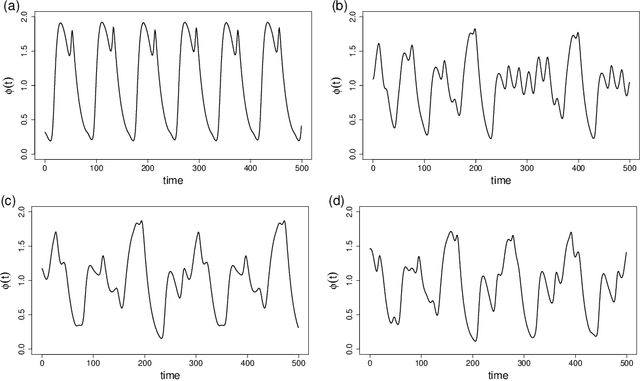
We propose a recurrent neural network for a "model-free" simulation of a dynamical system with unknown parameters without prior knowledge. The deep learning model aims to jointly learn the nonlinear time marching operator and the effects of the unknown parameters from a time series dataset. We assume that the time series data set consists of an ensemble of trajectories for a range of the parameters. The learning task is formulated as a statistical inference problem by considering the unknown parameters as random variables. A variational inference method is employed to train a recurrent neural network jointly with a feedforward neural network for an approximately posterior distribution. The approximate posterior distribution makes an inference on a trajectory to identify the effects of the unknown parameters and a recurrent neural network makes a prediction by using the outcome of the inference. In the numerical experiments, it is shown that the proposed variational inference model makes a more accurate simulation compared to the standard recurrent neural networks. It is found that the proposed deep learning model is capable of correctly identifying the dimensions of the random parameters and learning a representation of complex time series data.

DTN: A Learning Rate Scheme with Convergence Rate of $\mathcal{O}$ for SGD

We propose a novel diminishing learning rate scheme, coined Decreasing-Trend-Nature (DTN), which allows us to prove fast convergence of the Stochastic Gradient Descent (SGD) algorithm to a first-order stationary point for smooth general convex and some class of nonconvex including neural network applications for classification problems. We are the first to prove that SGD with diminishing learning rate achieves a convergence rate of $\mathcal{O}(1/t)$ for these problems. Our theory applies to neural network applications for classification problems in a straightforward way.

Optimal Finite-Sum Smooth Non-Convex Optimization with SARAH

The total complexity (measured as the total number of gradient computations) of a stochastic first-order optimization algorithm that finds a first-order stationary point of a finite-sum smooth nonconvex objective function $F(w)=\frac{1}{n} \sum_{i=1}^n f_i(w)$ has been proven to be at least $\Omega(\sqrt{n}/\epsilon)$ where $\epsilon$ denotes the attained accuracy $\mathbb{E}[ \|\nabla F(\tilde{w})\|^2] \leq \epsilon$ for the outputted approximation $\tilde{w}$ (Fang et al.,2018). This paper is the first to show that this lower bound is tight for the class of variance reduction methods which only assume the Lipschitz continuous gradient assumption. We prove this complexity result for a slightly modified version of the SARAH algorithm in (Nguyen et al.,2017a;b) - showing that SARAH is optimal and dominates all existing results. For convex optimization, we propose SARAH++ with sublinear convergence for general convex and linear convergence for strongly convex problems; and we provide a practical version for which numerical experiments on various datasets show an improved performance.

When Does Stochastic Gradient Algorithm Work Well?

In this paper, we consider a general stochastic optimization problem which is often at the core of supervised learning, such as deep learning and linear classification. We consider a standard stochastic gradient descent (SGD) method with a fixed, large step size and propose a novel assumption on the objective function, under which this method has the improved convergence rates (to a neighborhood of the optimal solutions). We then empirically demonstrate that these assumptions hold for logistic regression and standard deep neural networks on classical data sets. Thus our analysis helps to explain when efficient behavior can be expected from the SGD method in training classification models and deep neural networks.