Even Faster Hyperbolic Random Forests: A Beltrami-Klein Wrapper Approach

Decision trees and models that use them as primitives are workhorses of machine learning in Euclidean spaces. Recent work has further extended these models to the Lorentz model of hyperbolic space by replacing axis-parallel hyperplanes with homogeneous hyperplanes when partitioning the input space. In this paper, we show how the hyperDT algorithm can be elegantly reexpressed in the Beltrami-Klein model of hyperbolic spaces. This preserves the thresholding operation used in Euclidean decision trees, enabling us to further rewrite hyperDT as simple pre- and post-processing steps that form a wrapper around existing tree-based models designed for Euclidean spaces. The wrapper approach unlocks many optimizations already available in Euclidean space models, improving flexibility, speed, and accuracy while offering a simpler, more maintainable, and extensible codebase. Our implementation is available at https://github.com/pchlenski/hyperdt.

Manify: A Python Library for Learning Non-Euclidean Representations

We present Manify, an open-source Python library for non-Euclidean representation learning. Leveraging manifold learning techniques, Manify provides tools for learning embeddings in (products of) non-Euclidean spaces, performing classification and regression with data that lives in such spaces, and estimating the curvature of a manifold. Manify aims to advance research and applications in machine learning by offering a comprehensive suite of tools for manifold-based data analysis. Our source code, examples, datasets, results, and documentation are available at https://github.com/pchlenski/manify

Mixed-Curvature Decision Trees and Random Forests

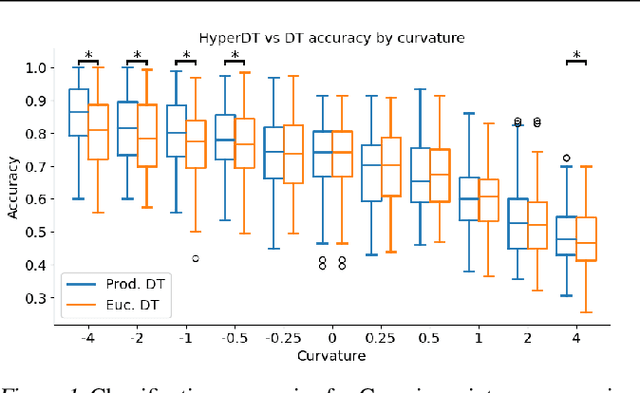
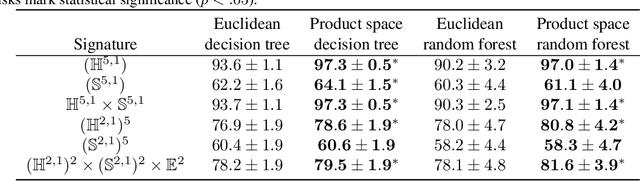
We extend decision tree and random forest algorithms to mixed-curvature product spaces. Such spaces, defined as Cartesian products of Euclidean, hyperspherical, and hyperbolic manifolds, can often embed points from pairwise distances with much lower distortion than in single manifolds. To date, all classifiers for product spaces fit a single linear decision boundary, and no regressor has been described. Our method overcomes these limitations by enabling simple, expressive classification and regression in product manifolds. We demonstrate the superior accuracy of our tool compared to Euclidean methods operating in the ambient space for component manifolds covering a wide range of curvatures, as well as on a selection of product manifolds.

Variational Pseudo Marginal Methods for Jet Reconstruction in Particle Physics

Reconstructing jets, which provide vital insights into the properties and histories of subatomic particles produced in high-energy collisions, is a main problem in data analyses in collider physics. This intricate task deals with estimating the latent structure of a jet (binary tree) and involves parameters such as particle energy, momentum, and types. While Bayesian methods offer a natural approach for handling uncertainty and leveraging prior knowledge, they face significant challenges due to the super-exponential growth of potential jet topologies as the number of observed particles increases. To address this, we introduce a Combinatorial Sequential Monte Carlo approach for inferring jet latent structures. As a second contribution, we leverage the resulting estimator to develop a variational inference algorithm for parameter learning. Building on this, we introduce a variational family using a pseudo-marginal framework for a fully Bayesian treatment of all variables, unifying the generative model with the inference process. We illustrate our method's effectiveness through experiments using data generated with a collider physics generative model, highlighting superior speed and accuracy across a range of tasks.

Distributional bias compromises leave-one-out cross-validation

Cross-validation is a common method for estimating the predictive performance of machine learning models. In a data-scarce regime, where one typically wishes to maximize the number of instances used for training the model, an approach called "leave-one-out cross-validation" is often used. In this design, a separate model is built for predicting each data instance after training on all other instances. Since this results in a single test data point available per model trained, predictions are aggregated across the entire dataset to calculate common rank-based performance metrics such as the area under the receiver operating characteristic or precision-recall curves. In this work, we demonstrate that this approach creates a negative correlation between the average label of each training fold and the label of its corresponding test instance, a phenomenon that we term distributional bias. As machine learning models tend to regress to the mean of their training data, this distributional bias tends to negatively impact performance evaluation and hyperparameter optimization. We show that this effect generalizes to leave-P-out cross-validation and persists across a wide range of modeling and evaluation approaches, and that it can lead to a bias against stronger regularization. To address this, we propose a generalizable rebalanced cross-validation approach that corrects for distributional bias. We demonstrate that our approach improves cross-validation performance evaluation in synthetic simulations and in several published leave-one-out analyses.

Fast hyperboloid decision tree algorithms

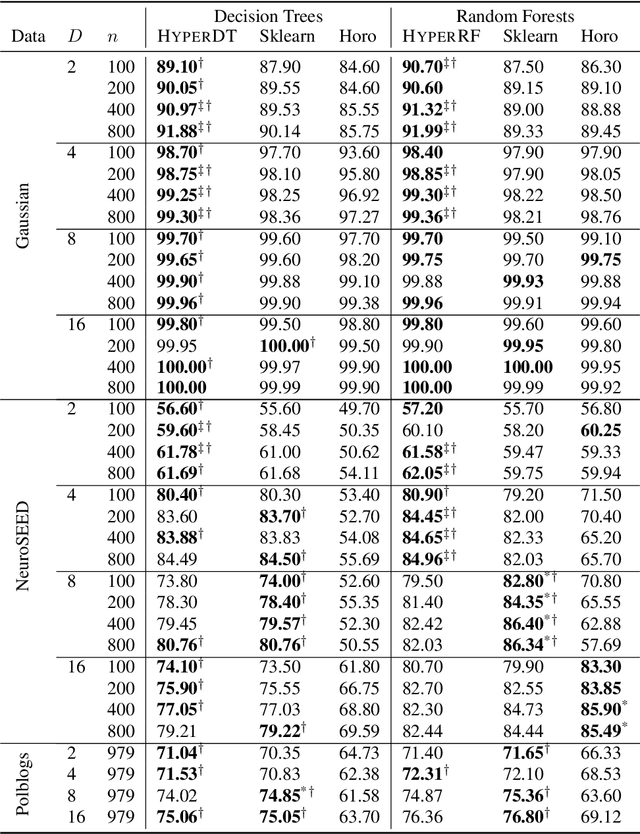
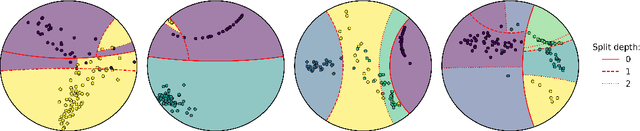
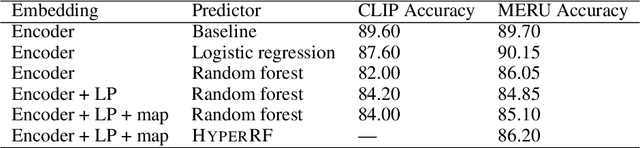
Hyperbolic geometry is gaining traction in machine learning for its effectiveness at capturing hierarchical structures in real-world data. Hyperbolic spaces, where neighborhoods grow exponentially, offer substantial advantages and consistently deliver state-of-the-art results across diverse applications. However, hyperbolic classifiers often grapple with computational challenges. Methods reliant on Riemannian optimization frequently exhibit sluggishness, stemming from the increased computational demands of operations on Riemannian manifolds. In response to these challenges, we present hyperDT, a novel extension of decision tree algorithms into hyperbolic space. Crucially, hyperDT eliminates the need for computationally intensive Riemannian optimization, numerically unstable exponential and logarithmic maps, or pairwise comparisons between points by leveraging inner products to adapt Euclidean decision tree algorithms to hyperbolic space. Our approach is conceptually straightforward and maintains constant-time decision complexity while mitigating the scalability issues inherent in high-dimensional Euclidean spaces. Building upon hyperDT we introduce hyperRF, a hyperbolic random forest model. Extensive benchmarking across diverse datasets underscores the superior performance of these models, providing a swift, precise, accurate, and user-friendly toolkit for hyperbolic data analysis.

Variational Combinatorial Sequential Monte Carlo Methods for Bayesian Phylogenetic Inference

Bayesian phylogenetic inference is often conducted via local or sequential search over topologies and branch lengths using algorithms such as random-walk Markov chain Monte Carlo (MCMC) or Combinatorial Sequential Monte Carlo (CSMC). However, when MCMC is used for evolutionary parameter learning, convergence requires long runs with inefficient exploration of the state space. We introduce Variational Combinatorial Sequential Monte Carlo (VCSMC), a powerful framework that establishes variational sequential search to learn distributions over intricate combinatorial structures. We then develop nested CSMC, an efficient proposal distribution for CSMC and prove that nested CSMC is an exact approximation to the (intractable) locally optimal proposal. We use nested CSMC to define a second objective, VNCSMC which yields tighter lower bounds than VCSMC. We show that VCSMC and VNCSMC are computationally efficient and explore higher probability spaces than existing methods on a range of tasks.

Accurate Protein Structure Prediction by Embeddings and Deep Learning Representations

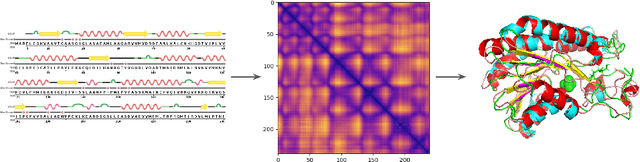
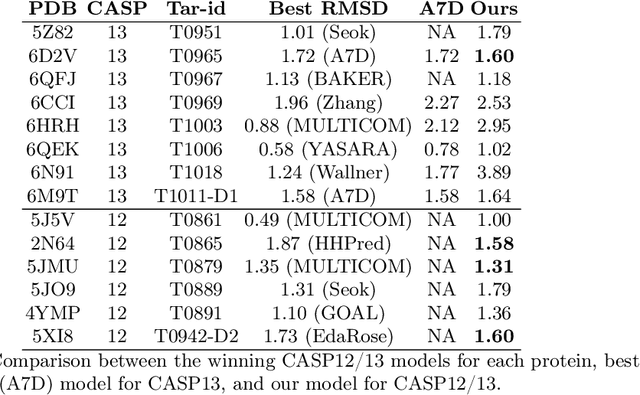
Proteins are the major building blocks of life, and actuators of almost all chemical and biophysical events in living organisms. Their native structures in turn enable their biological functions which have a fundamental role in drug design. This motivates predicting the structure of a protein from its sequence of amino acids, a fundamental problem in computational biology. In this work, we demonstrate state-of-the-art protein structure prediction (PSP) results using embeddings and deep learning models for prediction of backbone atom distance matrices and torsion angles. We recover 3D coordinates of backbone atoms and reconstruct full atom protein by optimization. We create a new gold standard dataset of proteins which is comprehensive and easy to use. Our dataset consists of amino acid sequences, Q8 secondary structures, position specific scoring matrices, multiple sequence alignment co-evolutionary features, backbone atom distance matrices, torsion angles, and 3D coordinates. We evaluate the quality of our structure prediction by RMSD on the latest Critical Assessment of Techniques for Protein Structure Prediction (CASP) test data and demonstrate competitive results with the winning teams and AlphaFold in CASP13 and supersede the results of the winning teams in CASP12. We make our data, models, and code publicly available.

Particle Smoothing Variational Objectives

A body of recent work has focused on constructing a variational family of filtered distributions using Sequential Monte Carlo (SMC). Inspired by this work, we introduce Particle Smoothing Variational Objectives (SVO), a novel backward simulation technique and smoothed approximate posterior defined through a subsampling process. SVO augments support of the proposal and boosts particle diversity. Recent literature argues that increasing the number of samples K to obtain tighter variational bounds may hurt the proposal learning, due to a signal-to-noise ratio (SNR) of gradient estimators decreasing at the rate $\mathcal{O}(1/\sqrt{K})$. As a second contribution, we develop theoretical and empirical analysis of the SNR in filtering SMC, which motivates our choice of biased gradient estimators. We prove that introducing bias by dropping Categorical terms from the gradient estimate or using Gumbel-Softmax mitigates the adverse effect on the SNR. We apply SVO to three nonlinear latent dynamics tasks and provide statistics to rigorously quantify the predictions of filtered and smoothed objectives. SVO consistently outperforms filtered objectives when given fewer Monte Carlo samples on three nonlinear systems of increasing complexity.

High Quality Prediction of Protein Q8 Secondary Structure by Diverse Neural Network Architectures

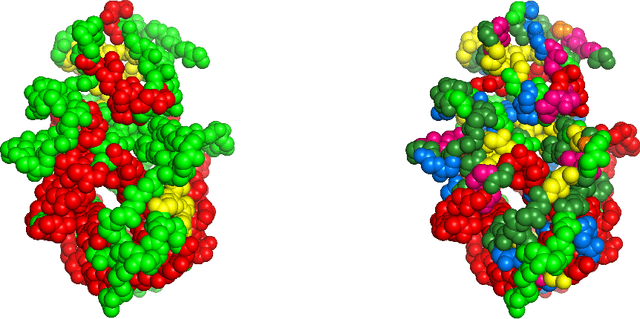
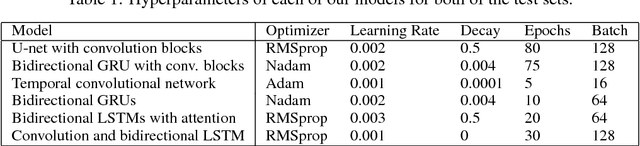
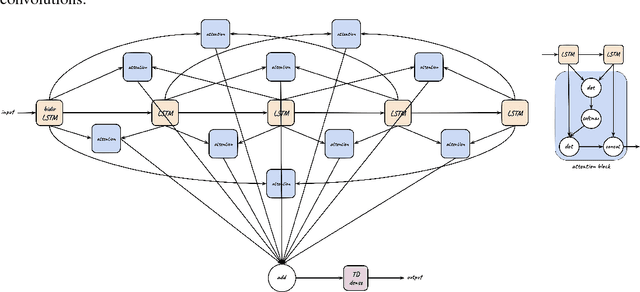
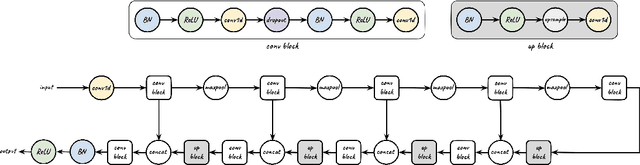
We tackle the problem of protein secondary structure prediction using a common task framework. This lead to the introduction of multiple ideas for neural architectures based on state of the art building blocks, used in this task for the first time. We take a principled machine learning approach, which provides genuine, unbiased performance measures, correcting longstanding errors in the application domain. We focus on the Q8 resolution of secondary structure, an active area for continuously improving methods. We use an ensemble of strong predictors to achieve accuracy of 70.7% (on the CB513 test set using the CB6133filtered training set). These results are statistically indistinguishable from those of the top existing predictors. In the spirit of reproducible research we make our data, models and code available, aiming to set a gold standard for purity of training and testing sets. Such good practices lower entry barriers to this domain and facilitate reproducible, extendable research.