Robust Explanations for Deep Neural Networks via Pseudo Neural Tangent Kernel Surrogate Models

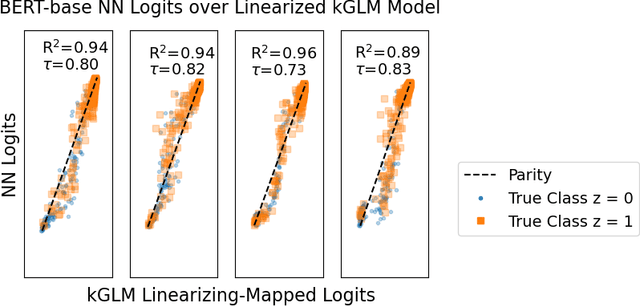
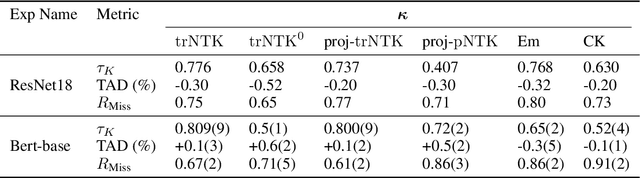
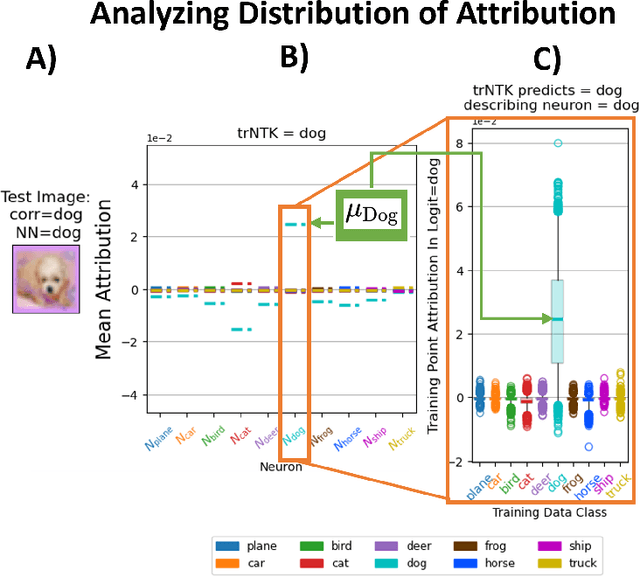
One of the ways recent progress has been made on explainable AI has been via explain-by-example strategies, specifically, through data attribution tasks. The feature spaces used to attribute decisions to training data, however, have not been compared against one another as to whether they form a truly representative surrogate model of the neural network (NN). Here, we demonstrate the efficacy of surrogate linear feature spaces to neural networks through two means: (1) we establish that a normalized psuedo neural tangent kernel (pNTK) is more correlated to the neural network decision functions than embedding based and influence based alternatives in both computer vision and large language model architectures; (2) we show that the attributions created from the normalized pNTK more accurately select perturbed training data in a data poisoning attribution task than these alternatives. Based on these observations, we conclude that kernel linear models are effective surrogate models across multiple classification architectures and that pNTK-based kernels are the most appropriate surrogate feature space of all kernels studied.

Exact recovery for the non-uniform Hypergraph Stochastic Block Model

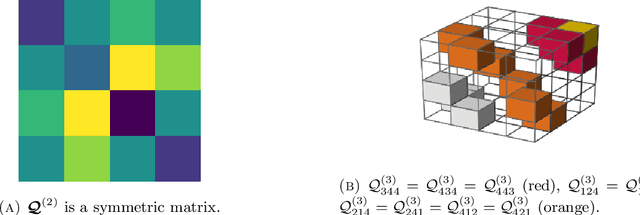
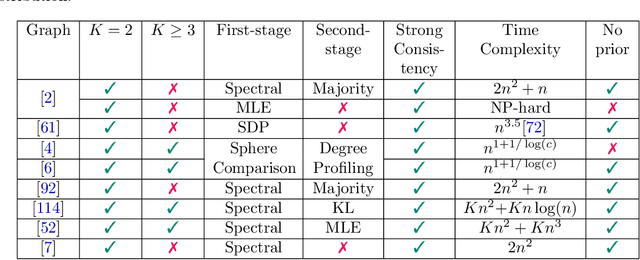
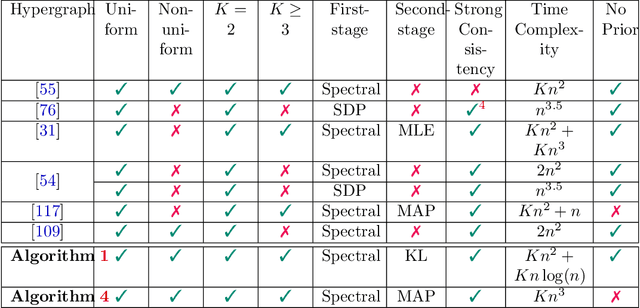
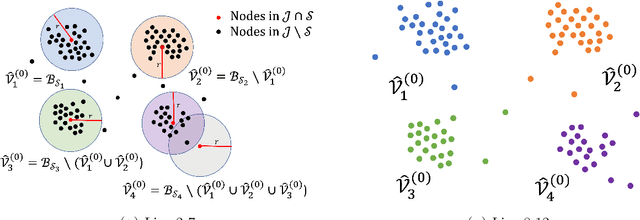
Consider the community detection problem in random hypergraphs under the non-uniform hypergraph stochastic block model (HSBM), where each hyperedge appears independently with some given probability depending only on the labels of its vertices. We establish, for the first time in the literature, a sharp threshold for exact recovery under this non-uniform case, subject to minor constraints; in particular, we consider the model with $K$ classes as well as the symmetric binary model ($K=2$). One crucial point here is that by aggregating information from all the uniform layers, we may obtain exact recovery even in cases when this may appear impossible if each layer were considered alone. Two efficient algorithms that successfully achieve exact recovery above the threshold are provided. The theoretical analysis of our algorithms relies on the concentration and regularization of the adjacency matrix for non-uniform random hypergraphs, which could be of independent interest. We also address some open problems regarding parameter knowledge and estimation.

Spectral evolution and invariance in linear-width neural networks

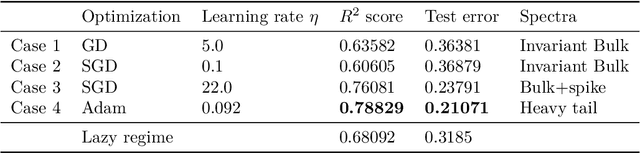
We investigate the spectral properties of linear-width feed-forward neural networks, where the sample size is asymptotically proportional to network width. Empirically, we show that the weight spectra in this high dimensional regime are invariant when trained by gradient descent for small constant learning rates and the changes in both operator and Frobenius norm are $\Theta(1)$ in the limit. This implies the bulk spectra for both the conjugate and neural tangent kernels are also invariant. We demonstrate similar characteristics for models trained with mini-batch (stochastic) gradient descent with small learning rates and provide a theoretical justification for this special scenario. When the learning rate is large, we show empirically that an outlier emerges with its corresponding eigenvector aligned to the training data structure. We also show that after adaptive gradient training, where we have a lower test error and feature learning emerges, both the weight and kernel matrices exhibit heavy tail behavior. Different spectral properties such as invariant bulk, spike, and heavy-tailed distribution correlate to how far the kernels deviate from initialization. To understand this phenomenon better, we focus on a toy model, a two-layer network on synthetic data, which exhibits different spectral properties for different training strategies. Analogous phenomena also appear when we train conventional neural networks with real-world data. Our results show that monitoring the evolution of the spectra during training is an important step toward understanding the training dynamics and feature learning.

Partial recovery and weak consistency in the non-uniform hypergraph Stochastic Block Model

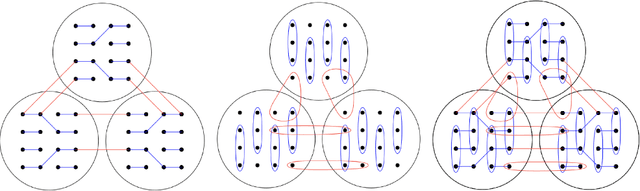
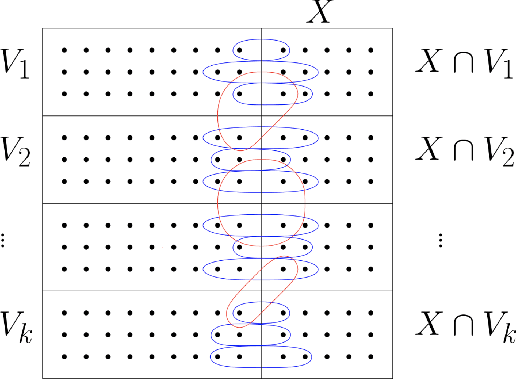
We consider the community detection problem in sparse random hypergraphs under the non-uniform hypergraph stochastic block model (HSBM), a general model of random networks with community structure and higher-order interactions. When the random hypergraph has bounded expected degrees, we provide a spectral algorithm that outputs a partition with at least a $\gamma$ fraction of the vertices classified correctly, where $\gamma\in (0.5,1)$ depends on the signal-to-noise ratio (SNR) of the model. When the SNR grows slowly as the number of vertices goes to infinity, our algorithm achieves weak consistency, which improves the previous results in Ghoshdastidar and Dukkipati (2017) for non-uniform HSBMs. Our spectral algorithm consists of three major steps: (1) Hyperedge selection: select hyperedges of certain sizes to provide the maximal signal-to-noise ratio for the induced sub-hypergraph; (2) Spectral partition: construct a regularized adjacency matrix and obtain an approximate partition based on singular vectors; (3) Correction and merging: incorporate the hyperedge information from adjacency tensors to upgrade the error rate guarantee. The theoretical analysis of our algorithm relies on the concentration and regularization of the adjacency matrix for sparse non-uniform random hypergraphs, which can be of independent interest.

Relative Density and Exact Recovery in Heterogeneous Stochastic Block Models

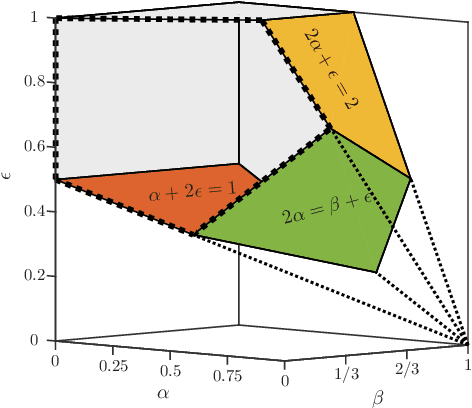
The Stochastic Block Model (SBM) is a widely used random graph model for networks with communities. Despite the recent burst of interest in recovering communities in the SBM from statistical and computational points of view, there are still gaps in understanding the fundamental information theoretic and computational limits of recovery. In this paper, we consider the SBM in its full generality, where there is no restriction on the number and sizes of communities or how they grow with the number of nodes, as well as on the connection probabilities inside or across communities. This generality allows us to move past the artifacts of homogenous SBM, and understand the right parameters (such as the relative densities of communities) that define the various recovery thresholds. We outline the implications of our generalizations via a set of illustrative examples. For instance, $\log n$ is considered to be the standard lower bound on the cluster size for exact recovery via convex methods, for homogenous SBM. We show that it is possible, in the right circumstances (when sizes are spread and the smaller the cluster, the denser), to recover very small clusters (up to $\sqrt{\log n}$ size), if there are just a few of them (at most polylogarithmic in $n$).